Floyd– Warshall algorithm презентация
Содержание
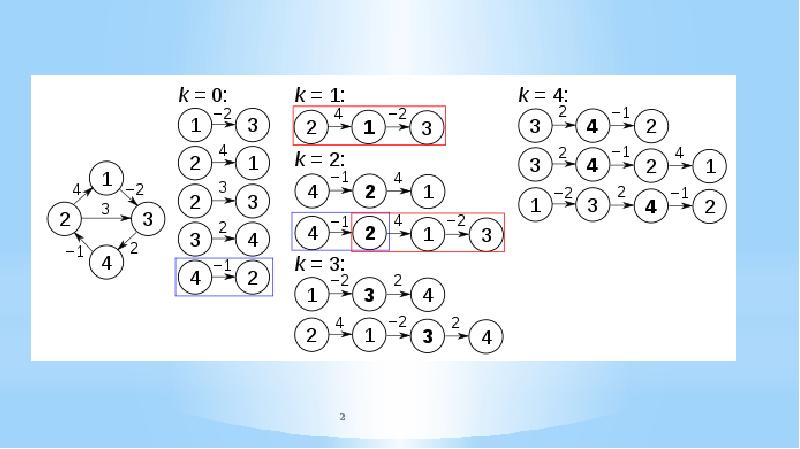
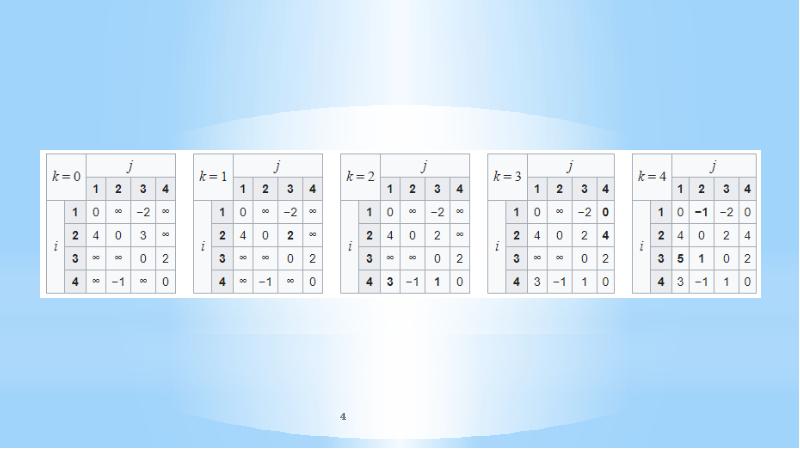
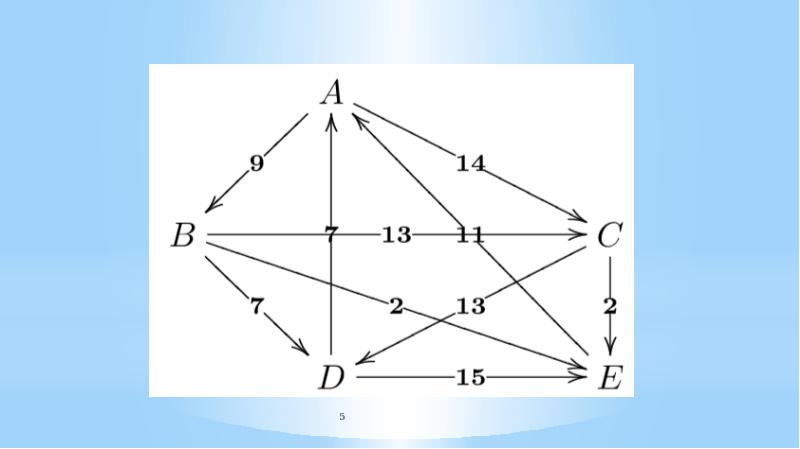
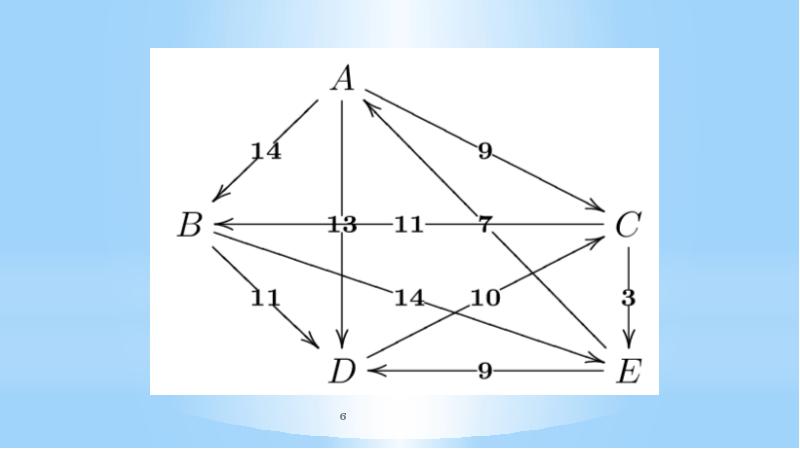
- 3. Prior to the first iteration of the outer loop, labeled k = 0 above,
- 12. 1. Prove that of six people, you can choose either three
- 13. 4. Visit all the cells of the chessboard 8х8 by the
- 16. Selection sort is an in-place comparison sort. The algorithm finds the
- 18. Radix sort is an algorithm that sorts numbers by processing individual
- 23. Скачать презентацию
















Слайды и текст этой презентации
Похожие презентации





























