Introduction to Vectors презентация

Introduction to Vectors Karashbayeva Zh.O.

What are Vectors? Vectors are pairs of a direction and a magnitude. We usually represent a vector with an arrow:

Vectors in Rn

Multiples of Vectors Given a real number c, we can multiply a vector by c by multiplying its magnitude by c:

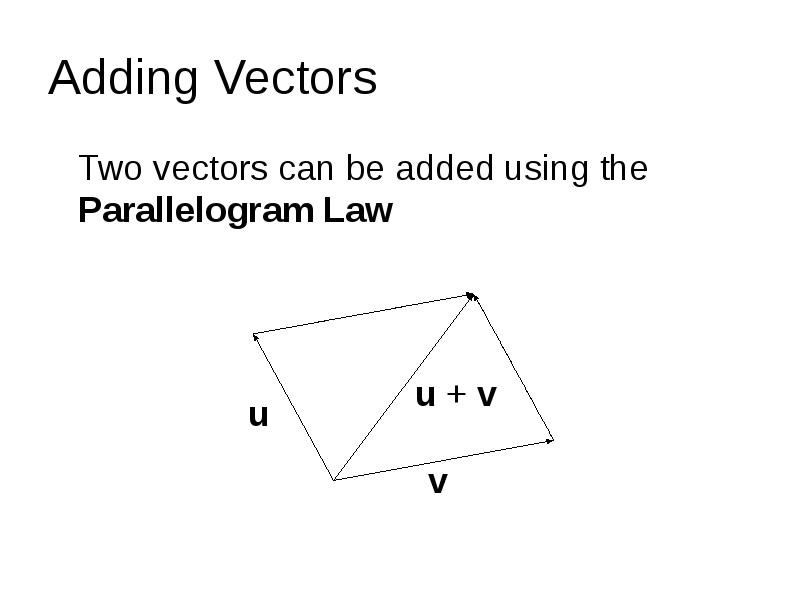
Adding Vectors Two vectors can be added using the Parallelogram Law

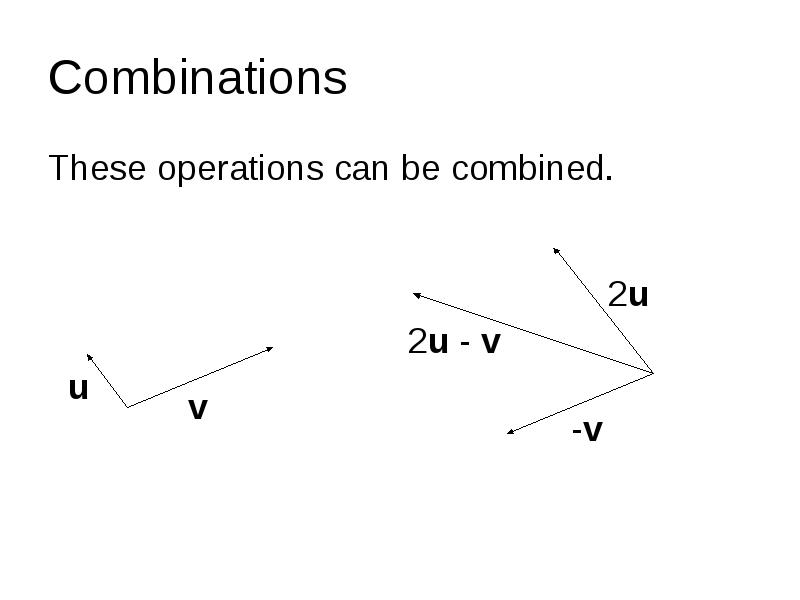
Combinations These operations can be combined.

Components To do computations with vectors, we place them in the plane and find their components.

Components The initial point is the tail, the head is the terminal point. The components are obtained by subtracting coordinates of the initial point from those of the terminal point.

Components The first component of v is 5 -2 = 3. The second is 6 -2 = 4. We write v = <3,4>

Magnitude The magnitude of the vector is the length of the segment, it is written ||v||.

Scalar Multiplication Once we have a vector in component form, the arithmetic operations are easy. To multiply a vector by a real number, simply multiply each component by that number. Example: If v = <3,4>, -2v = <-6,-8>

Addition To add vectors, simply add their components. For example, if v = <3,4> and w = <-2,5>, then v + w = <1,9>. Other combinations are possible. For example: 4v – 2w = <16,6>.

Unit Vectors A unit vector is a vector with magnitude 1. Given a vector v, we can form a unit vector by multiplying the vector by 1/||v||. For example, find the unit vector in the direction <3,4>:

Special Unit Vectors A vector such as <3,4> can be written as 3<1,0> + 4<0,1>. For this reason, these vectors are given special names: i = <1,0> and j = <0,1>. A vector in component form v = <a,b> can be written ai + bj.

Spanning Sets and Linear Independence

EX: Testing for linear independence EX: Testing for linear independence Determine whether the following set of vectors in P2 is L.I. or L.D.

Basis and Dimension Basis :