Rijndael презентация

Rijndael Advanced Encryption Standard (AES)

Rijndael Разрабатывается стандарт AES MARS от группы при IBM RS6 от RSA Security Twofish от базирующейся в Коунтерпэйне, Беркли Serpent три ученых –Израиль, Норвегия, Британия Rijndael – бельгийские криптографы. Итерированное блочное шифрование – стойкость обеспечивается повторяющейся раундовой функцией – преобразующей n-битовые блоки в n- битовые блоки, n размер блока шифра.

Основные математические понятия, используемые в алгоритме. Байт b, состоящий из битов b7, b6, b5, b4, b3, b2, b1, b0, представляется в виде полинома с коэффициентами из {0, 1}: b7х7 + b6х6 + b5х5 + b4х4 + b3х3 + b2х2 + b1х1 + b0 Пример: Байт с шестнадцатеричным значением '57' (двоичное 01010111) соответствует полиному х6 + х4 + х2 + х + 1

Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов. Конечное поле обычно обозначается GF(q), где q — число элементов поля.

Сложение. Пример: '57' + '83' = 'D4' или в виде полинома: (х^6 + х^4 + х^2 + х + 1) + (х^7 + х + 1) = =х^7 + х^6 + х^4 + х^2 В бинарной нотации мы имеем: 01010111 + 10000011 = 11010100. Сложение соответствует простому XOR (обозначается как ) на уровне байта.

Умножение В полиномиальном представлении умножение в GF (2^8) соответствует умножению полиномов по модулю неприводимого двоичного полинома степени 8. Полином является неприводимым, если он не имеет делителей, кроме 1 и самого себя. Для Rijndael такой полином называется m(x) и определяется следующим образом: m(x) = x^8 + x^4 + x^3 + x + 1 или '11B' в шестнадцатеричном представлении. Пример: '57' • '83' = 'C1' или (x^6 + x^4 + x^2 + х + 1) (x^7 + х + 1) = x^13 + x^11 + x^9 + x^8 + x^7 + x^7 + x^5 + x^3 + x^2 + x + x^6 + x^4 + x^2 + х + 1 = x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 + 1 (x^8 + x^4 + x^3 + х + 1) (x^5 + x^3) + x^7 + x^6 + 1 = x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 +1 Следовательно, (x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^8 + 1) mod (x^8 + x^4 + x^3 + х + 1) = x^7 + x^6 + 1

Умножение на х. Если умножить b(x) на полином х, получится: b_7*x^8 + b_6*x^7 + b_5*x^6 + b_4*x^5 + b_3*x^4 + b_2*x^3 + b_1*x^2 + b_0*x x • b(x) получается понижением предыдущего результата по модулю m(x). Если b_7 = 0, то данное понижение является тождественной операцией. Если b_7 = 1, m(x) следует вычесть (т.е. XORed).

Разработка алгоритма При разработке алгоритма учитывались следующие три критерия: противодействие всем известным атакам; скорость и компактность кода для широкого круга платформ; простота разработки.

Состояние, ключ шифрования и число раундов Rijndael является блочным алгоритмом шифрования с переменной длиной блока и переменной длиной ключа. Длина блока и длина ключа могут быть независимо установлены в 128, 192 или 256 бит.

Состояние, ключ шифрования и число раундов Состояние можно рассматривать как двумерный массив байтов. Этот массив имеет четыре строки и различное число столбцов, обозначаемое как Nb, равное длине блока, деленной на 32. Ключ также можно рассматривать как двумерный массив с четырьмя строками. Число столбцов ключа шифрования, обозначаемое как Nk, равно длине ключа, деленной на 32. Число раундов обозначается Nr и зависит от значений Nb и Nk, что показано в следующей таблице.

Состояние, ключ шифрования и число раундов

Преобразование раунда

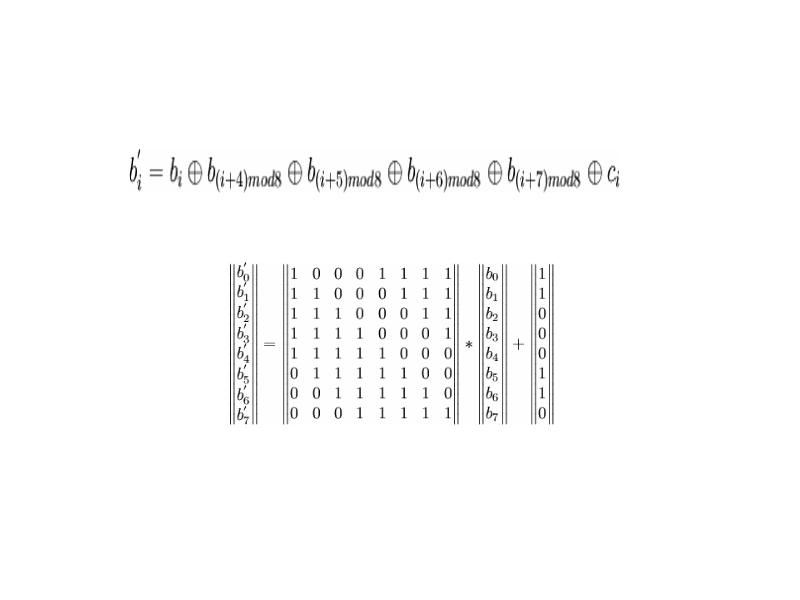
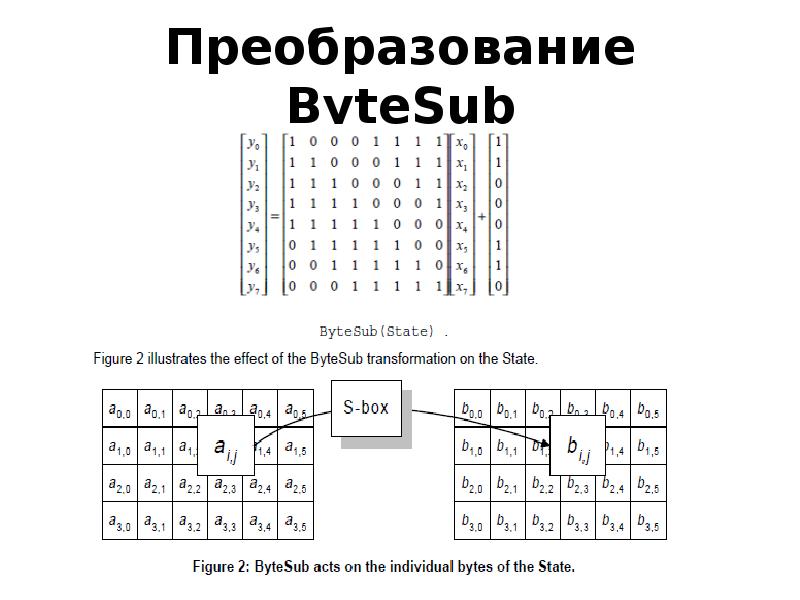
Преобразование ByteSub Преобразование ByteSub является нелинейной байтовой подстановкой, выполняющейся для каждого байта состояния независимо. Таблица подстановки является обратимой и сконструирована в виде композиции двух преобразований: Берется мультипликативная инверсия в GF (28) с определенным выше представлением. '00' отображается сам в себя. Применяется преобразование, определяемое следующим образом:

Преобразование ByteSub

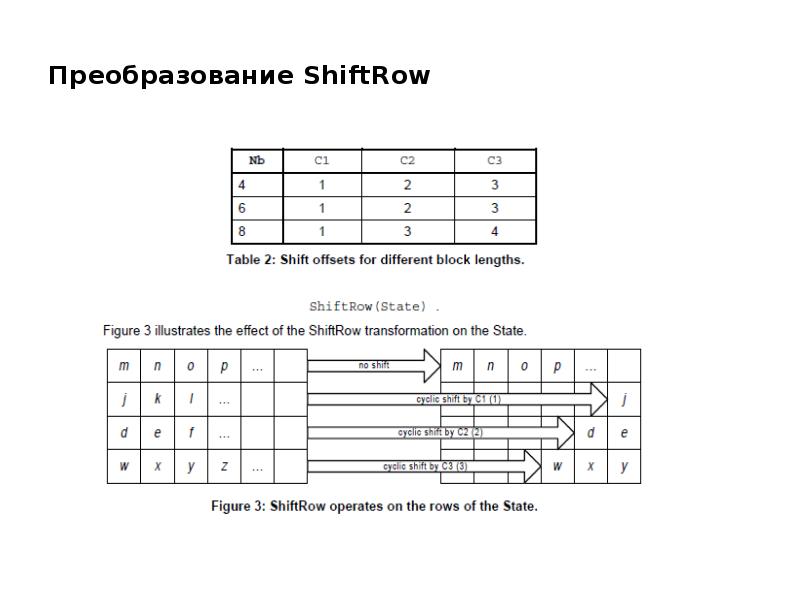
Преобразование ShiftRow

Преобразование MixColumn В MixColumn столбцы состояния рассматриваются как полиномы в GF (28) и умножаются по модулю х4 + 1 на фиксированный полином: c(x) = '03' x3 + '01' x2 + '01' x + '02'

Преобразование MixColumn

Сложение с ключом раунда Выполняется операция побитового XOR ключа раунда с текущим состоянием. Длина ключа раунда равна длине блока Nb. Данное преобразование обозначается как AddRoundKey (State, RoundKey) Ключи раунда получаются из ключа шифрования с помощью преобразования, состоящего из двух компонентов: расширение ключа и выбор ключа раунда. Основной принцип состоит в следующем: Общее число битов ключа раунда равно длине блока, умноженной на количество раундов плюс 1. Например, для длины блока 128 бит и 10 раундов необходимо 1408 битов ключа раунда. Ключ шифрования расширяется в ExpandedKey. Ключи раунда получаются из этого ExpandedKey следующим способом: первый ключ раунда состоит из первых Nb слов, второй состоит из следующих Nb слов и т.д.

Алгоритм шифрования Алгоритм шифрования Rijndael состоит из начального сложения с ключом; Nr - 1 раундов; заключительного раунда. В С-подобном представлении это выглядит так: Rijndael (State, CipherKey) { KeyExpansion (CipherKey, ExpandedKey); AddRoundKey (State, ExpandedKey); for (i=1; i < Nr; i++) Round (State, ExpandedKey + Nb*i); FinalRound (State, ExpandedKey + Nb*Nr)}

Алгоритм шифрования Расширение ключа может быть выполнено заранее, и Rijndael может быть специфицирован в терминах расширенного ключа. Rijndael (State, ExpandedKey) { AddRoundKey (State, ExpandedKey); for (i=1; i < Nr; i++) Round (State, ExpandedKey + Nb*i); FinalRound (State, ExpandedKey + Nb*Nr)} Расширенный ключ всегда получается из ключа шифрования и никогда не специфицируется непосредственно. На выбор самого ключа шифрования ограничений не существует.

Преимущества, относящиеся к аспектам реализации: Rijndael может выполняться быстрее, чем обычный блочный алгоритм шифрования. Выполнена оптимизация между размером таблицы и скоростью выполнения. Rijndael можно реализовать в смарт-карте в виде кода, используя небольшой RAM и имея небольшое число циклов. Выполнена оптимизация размера ROM и скорости выполнения. Преобразование раунда допускает параллельное выполнение, что является важным преимуществом для будущих процессоров и специализированной аппаратуры. Алгоритм шифрования не использует арифметические операции, поэтому тип архитектуры процессора не имеет значения.

Простота разработки: Алгоритм шифрования полностью "самоподдерживаемый". Он не использует других криптографических компонентов. Алгоритм не основывает свою безопасность или часть ее на неясностях или плохо понимаемых итерациях арифметических операций. Компактная разработка алгоритма не дает возможности спрятать люки.