The Tree Data Structure презентация
Содержание
- 2. Outline In this topic, we will cover: Definition of a tree
- 3. The Tree Data Structure Trees are the first data structure different
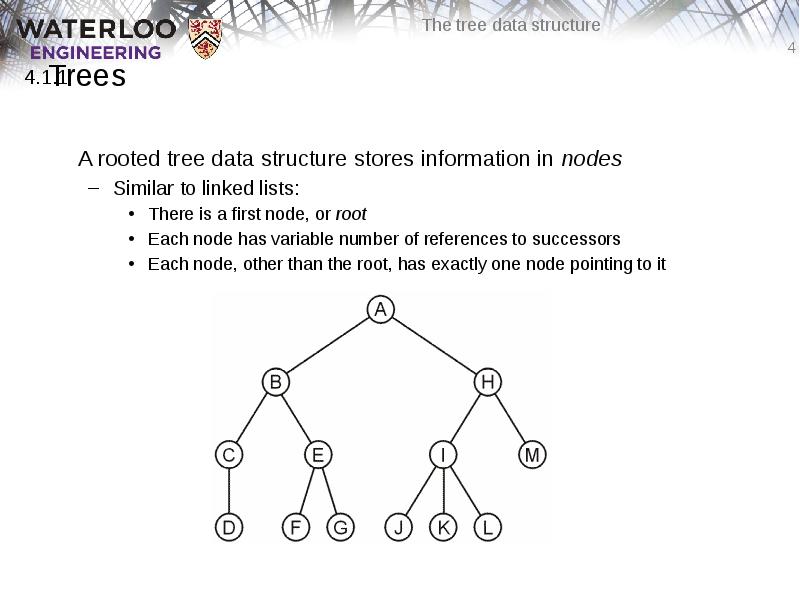
- 4. Trees A rooted tree data structure stores information in nodes Similar
- 5. Terminology All nodes will have zero or more child nodes or
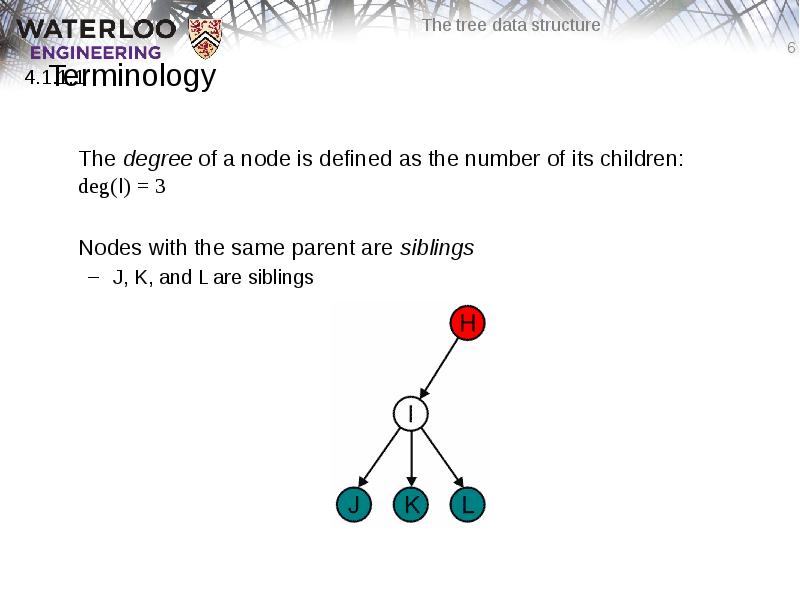
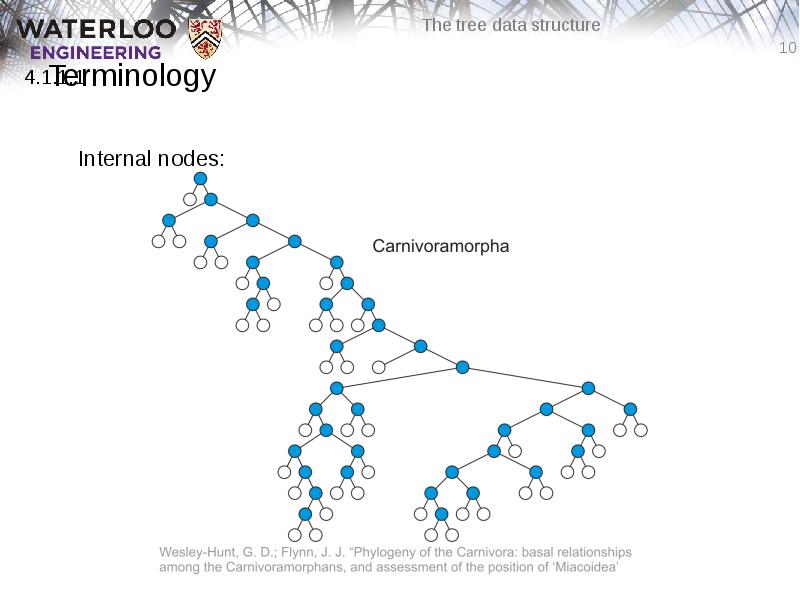
- 6. Terminology The degree of a node is defined as the number
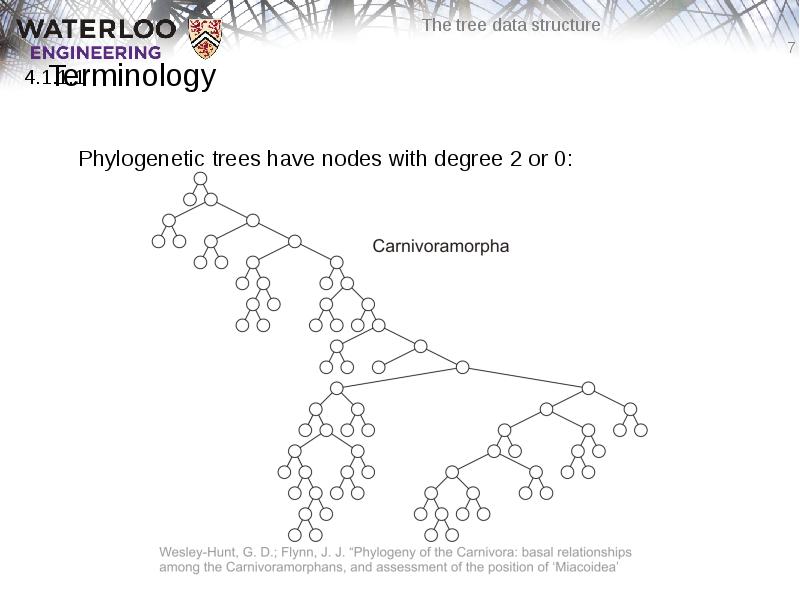
- 7. Terminology Phylogenetic trees have nodes with degree 2 or 0:
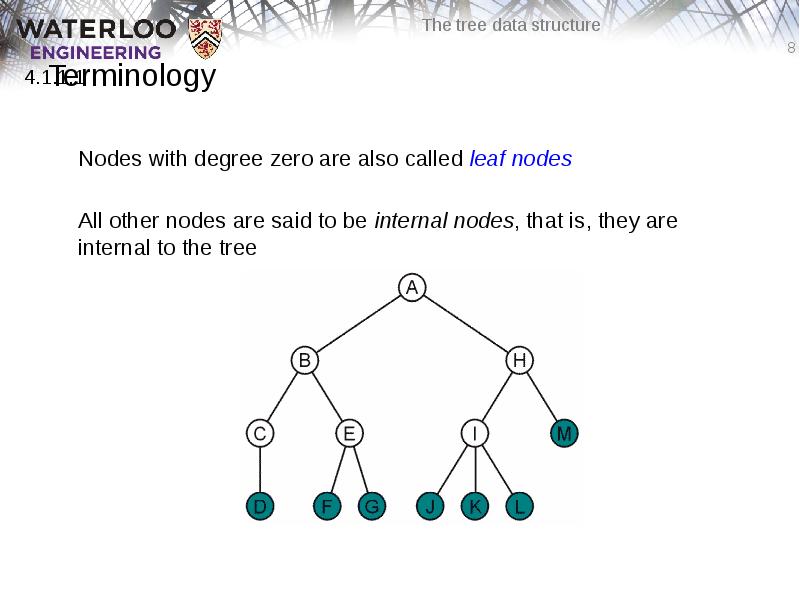
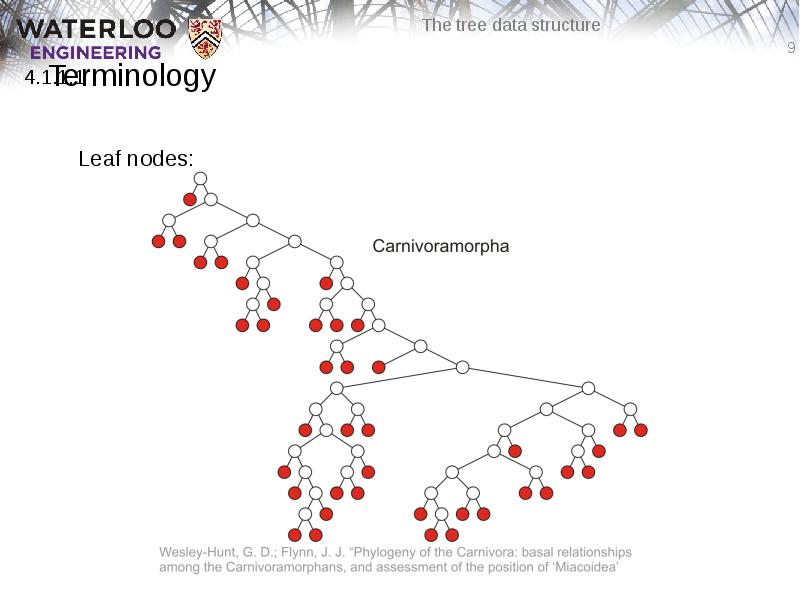
- 8. Terminology Nodes with degree zero are also called leaf nodes
- 9. Terminology Leaf nodes:
- 10. Terminology Internal nodes:
- 11. Terminology These trees are equal if the order of the children
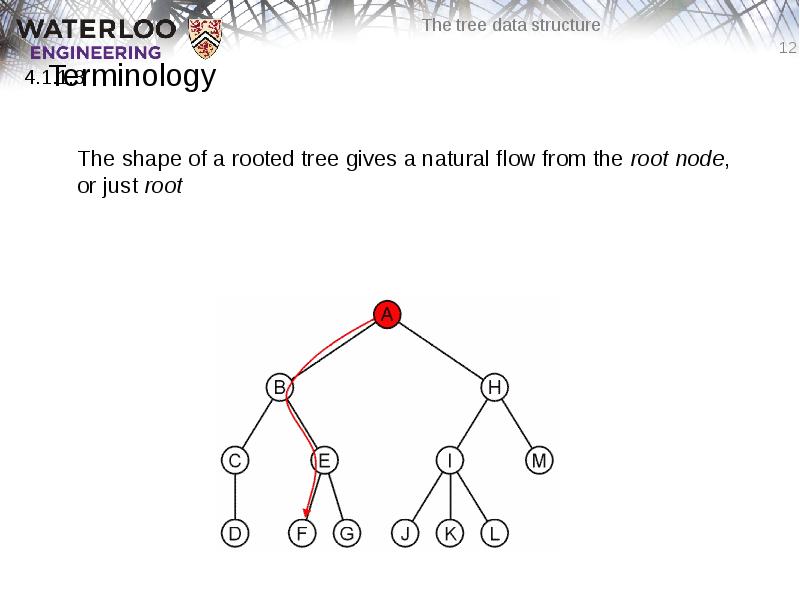
- 12. Terminology The shape of a rooted tree gives a natural flow
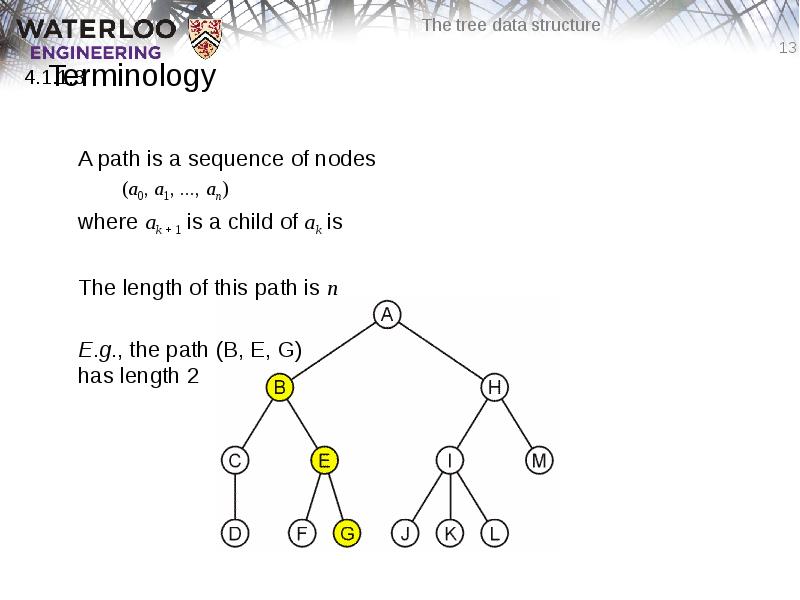
- 13. Terminology A path is a sequence of nodes (a0, a1,
- 14. Terminology Paths of length 10 (11 nodes) and 4 (5 nodes)
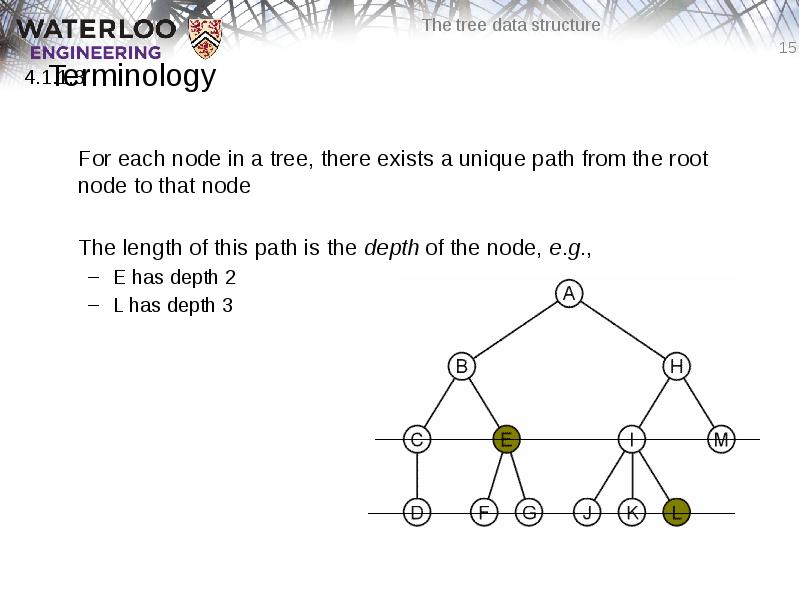
- 15. Terminology For each node in a tree, there exists a unique
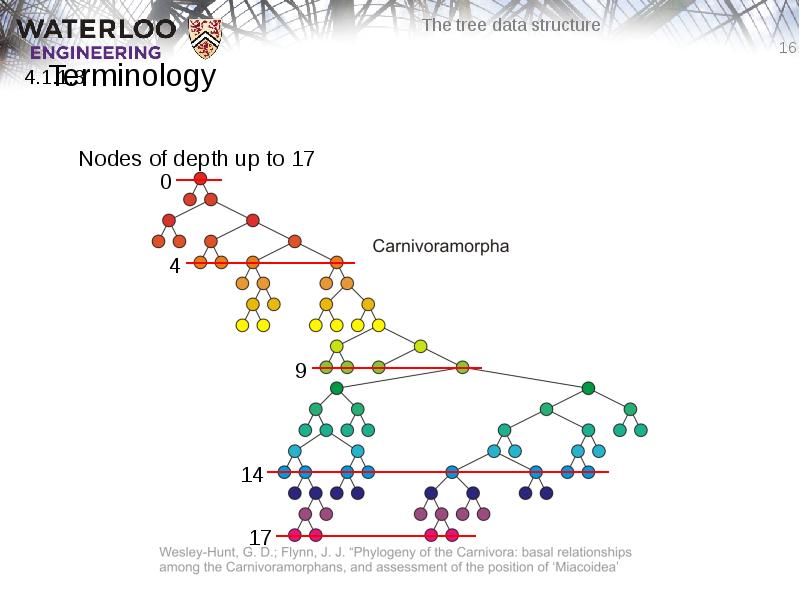
- 16. Terminology Nodes of depth up to 17
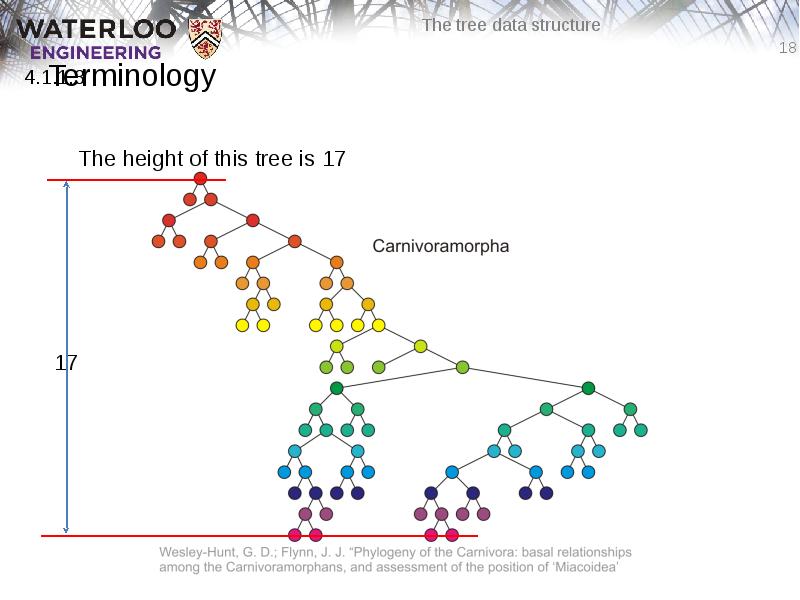
- 17. Terminology The height of a tree is defined as the maximum
- 18. Terminology The height of this tree is 17
- 19. Terminology If a path exists from node a to node b:
- 20. Terminology The descendants of node B are B, C, D, E,
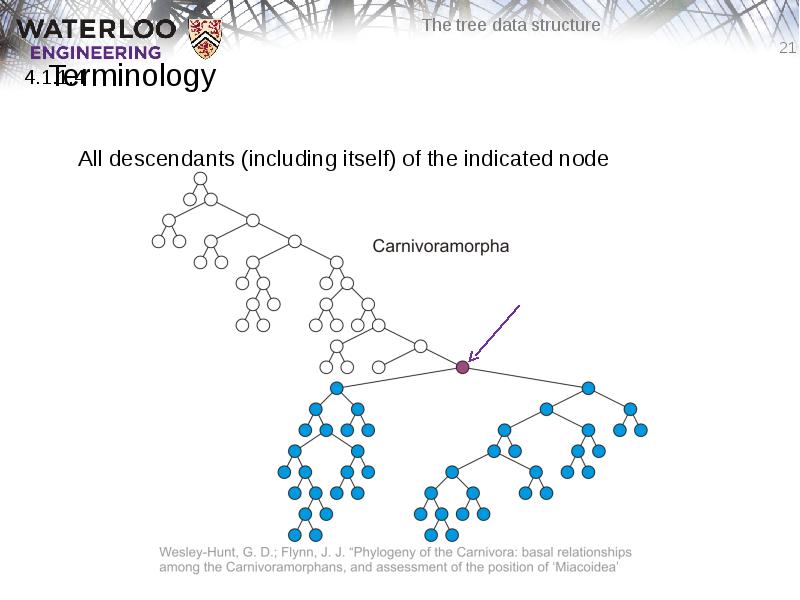
- 21. Terminology All descendants (including itself) of the indicated node
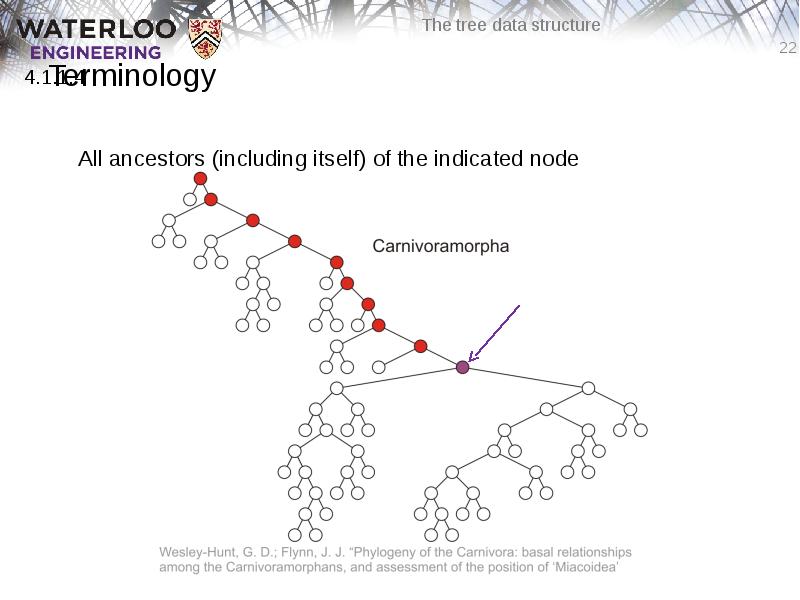
- 22. Terminology All ancestors (including itself) of the indicated node
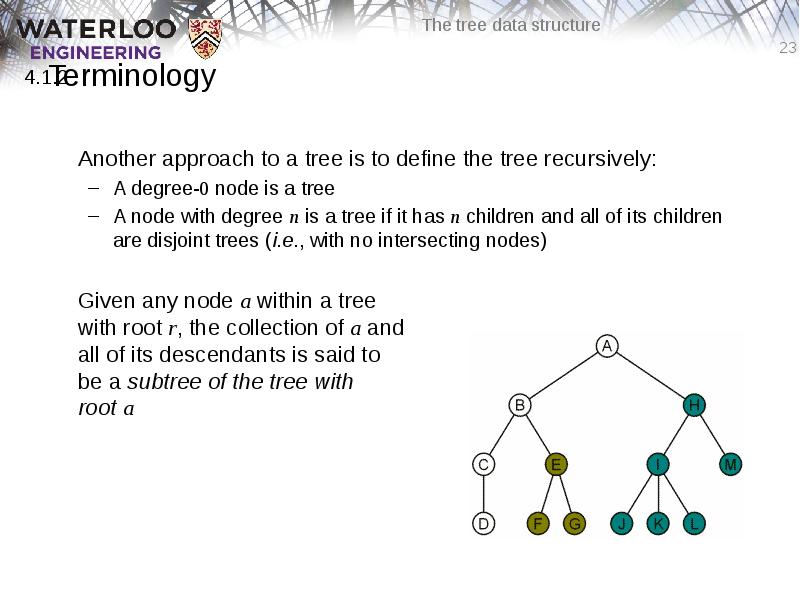
- 23. Terminology Another approach to a tree is to define the tree
- 24. Example: XHTML and CSS The XML of XHTML has a tree
- 25. Example: XHTML and CSS Consider the following XHTML document <html>
- 26. Example: XHTML and CSS Consider the following XHTML document <html>
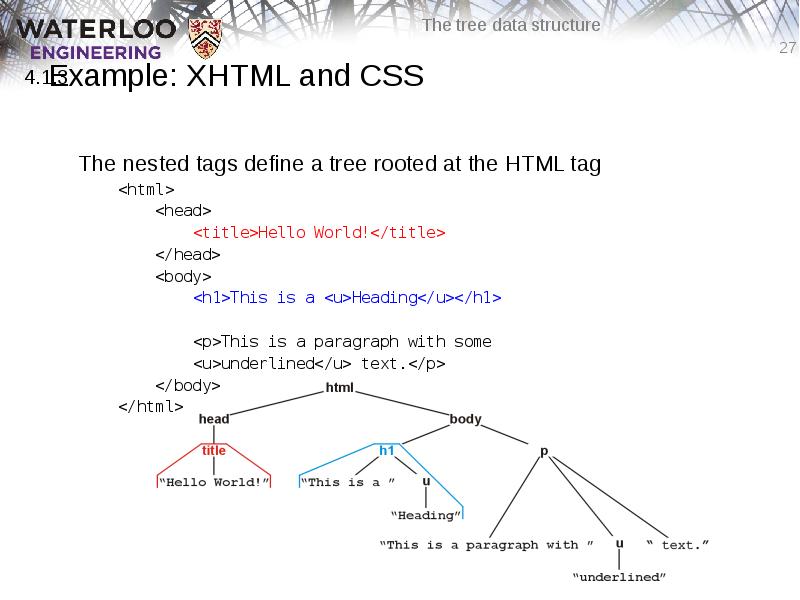
- 27. Example: XHTML and CSS The nested tags define a tree rooted
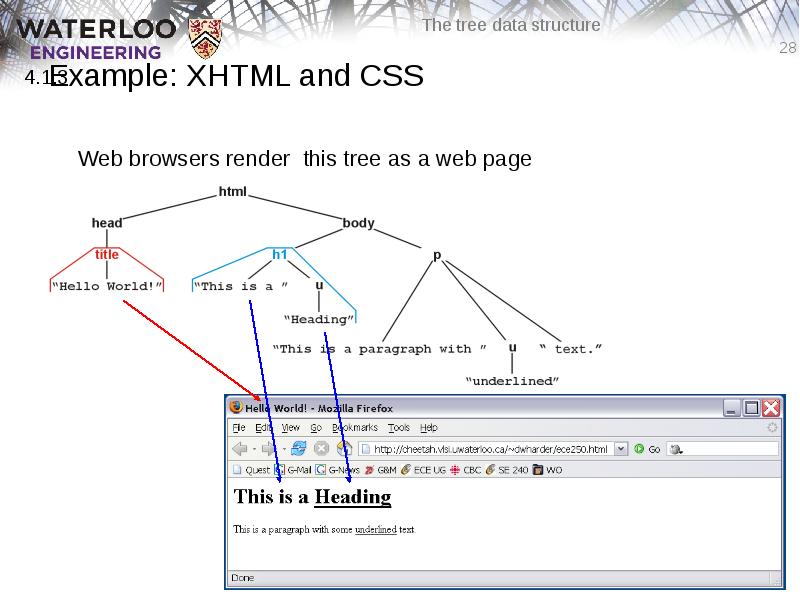
- 28. Example: XHTML and CSS Web browsers render this tree as a
- 29. Example: XHTML and CSS XML tags <tag>...</tag> must be nested For
- 30. Example: XHTML and CSS Cascading Style Sheets (CSS) make use of
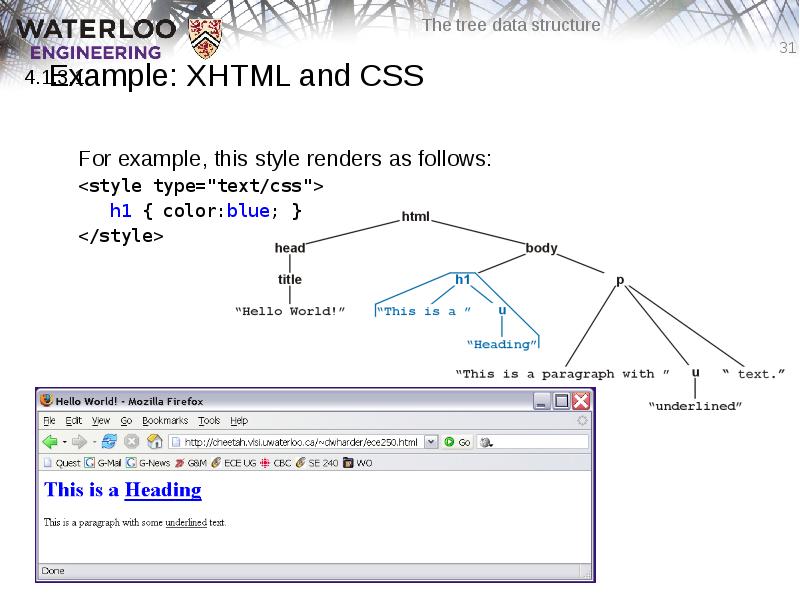
- 31. Example: XHTML and CSS For example, this style renders as follows:
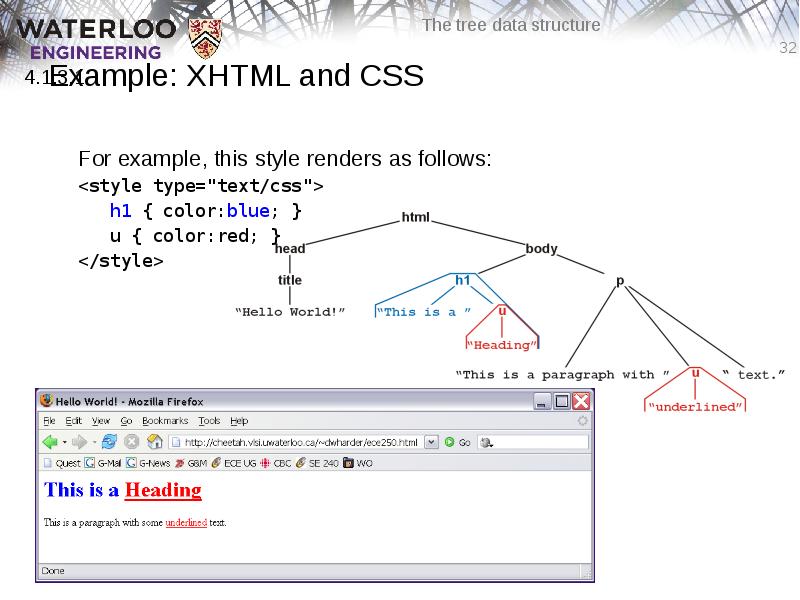
- 32. Example: XHTML and CSS For example, this style renders as follows:
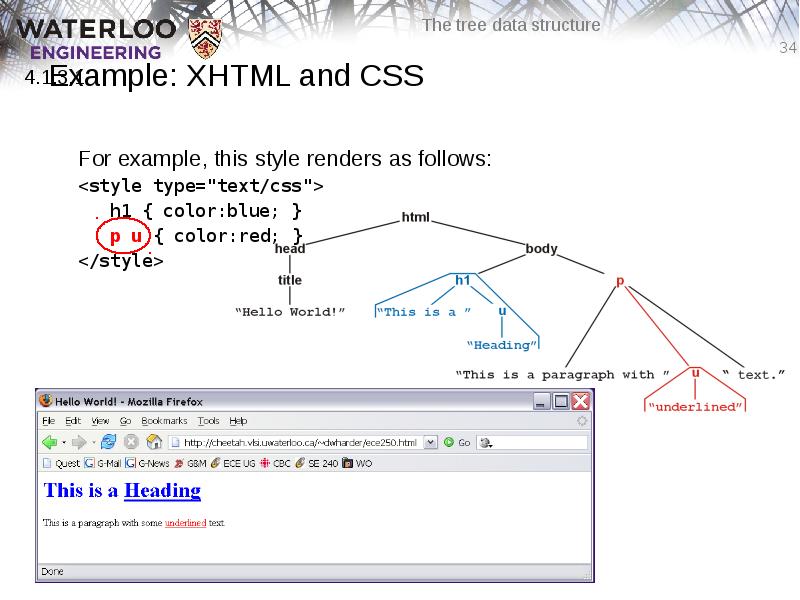
- 33. Example: XHTML and CSS Suppose you don’t want underlined items in
- 34. Example: XHTML and CSS For example, this style renders as follows:
- 35. Example: XHTML and CSS You can read the second style
- 36. Example: XML In general, any XML can be represented as a
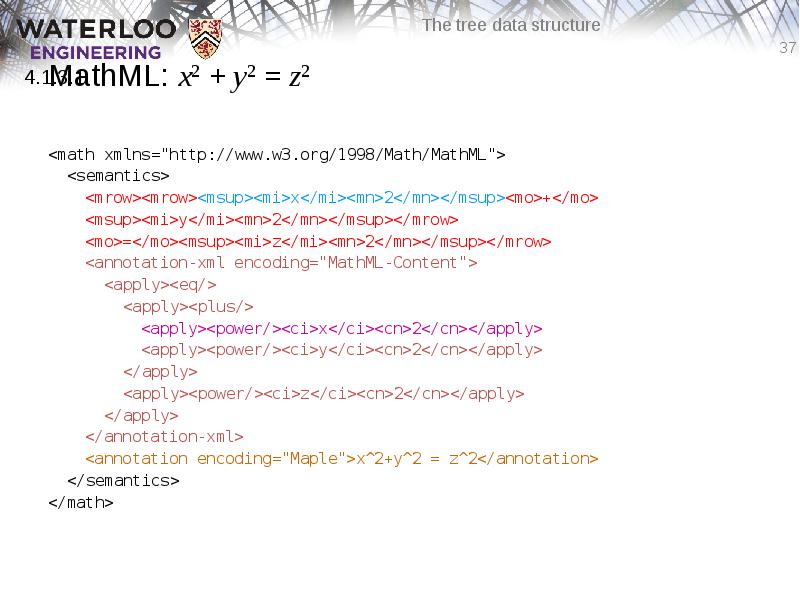
- 37. MathML: x2 + y2 = z2 <math xmlns="http://www.w3.org/1998/Math/MathML"> <semantics> <mrow><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo>
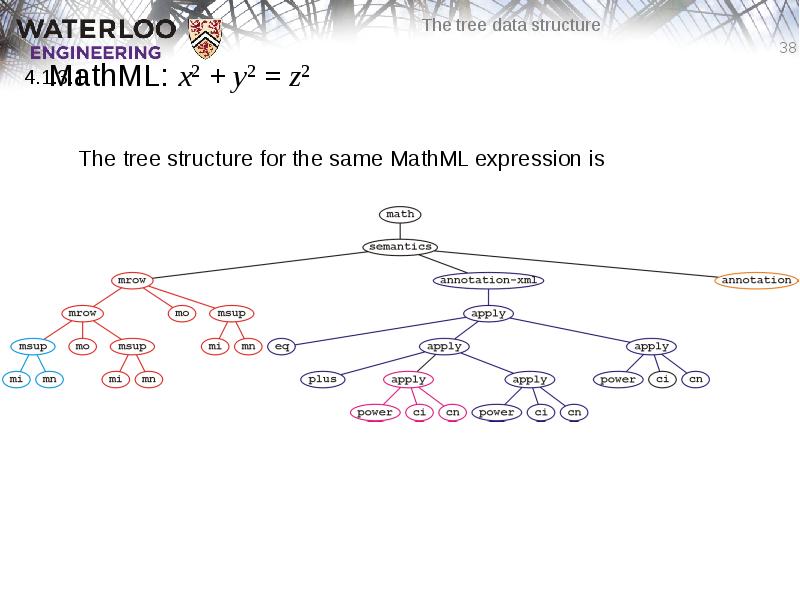
- 38. MathML: x2 + y2 = z2 The tree structure for the
- 39. MathML: x2 + y2 = z2 Why use 500 characters to
- 40. Summary In this topic, we have: Introduced the terminology used for
- 41. References [1] Donald E. Knuth, The Art of Computer Programming, Volume 1:
- 42. Usage Notes These slides are made publicly available on the web
- 43. Скачать презентацию



















![References
[1] Donald E. Knuth, The Art of Computer Programming, Volume 1: References
[1] Donald E. Knuth, The Art of Computer Programming, Volume 1:](/documents_7/75ca28ff685f408177a364e31a7786cb/img40.jpg)

Слайды и текст этой презентации
Похожие презентации





























