Анализ взаимосвязи социально-экономических явлений презентация
Содержание
- 2. Источники получения данных Социально-экономические явления представляют собой результат
- 3. Источники получения данных Признаки по их значению для
- 4. Источники получения данных Если причинная зависимость проявляется не
- 5. Спецификация модели Исследование социально-экономических явлений начинается с теории,
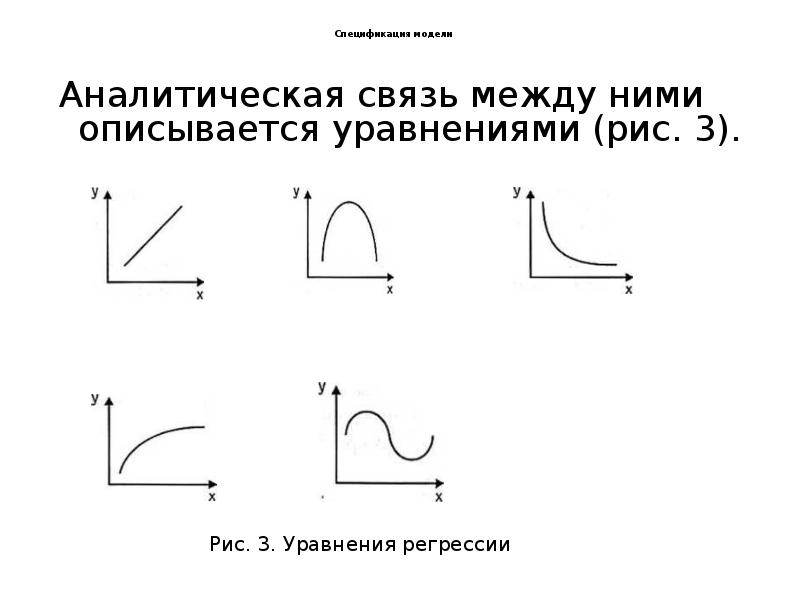
- 6. Спецификация модели Аналитическая связь между ними описывается уравнениями (рис.
- 7. Графическое изображение параметров уравнения Если результативный и факторный признаки
- 8. Метод наименьших квадратов Классический подход по оцениванию параметров
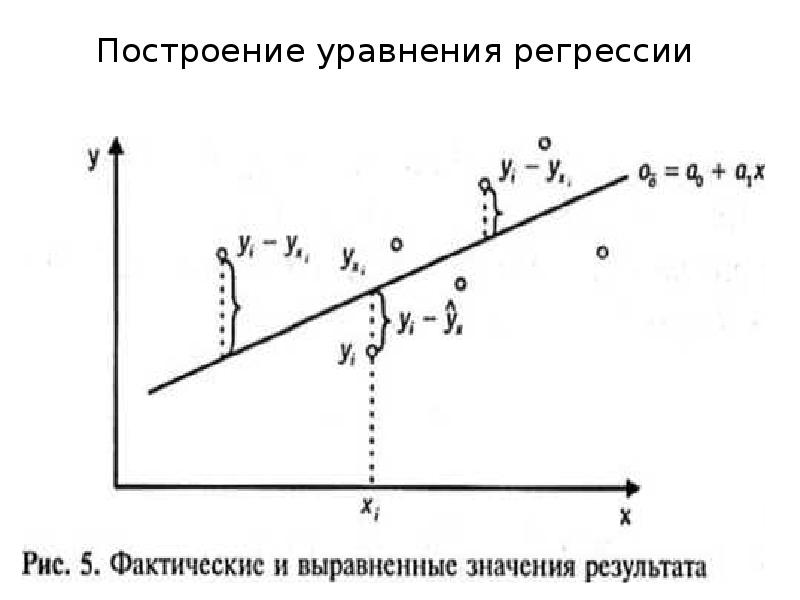
- 9. Построение уравнения регрессии
- 10. Метод наименьших квадратов После преобразования получим следующую систему
- 11. Метод наименьших квадратов Значимость коэффициента регрессии осуществляют с
- 12. Метод наименьших квадратов Для статистической оценки тесноты связи
- 13. Метод наименьших квадратов 3) остаточная дисперсия а2с, отображающая вариацию
- 14. Метод наименьших квадратов Соотношение между факторной и общей
- 15. Скачать презентацию












Слайды и текст этой презентации
Скачать презентацию на тему Анализ взаимосвязи социально-экономических явлений можно ниже:
Похожие презентации





























