Четырехугольники, вписанные в окружность. Теорема Птолемея презентация

Четырехугольники, вписанные в окружность. Теорема Птолемея

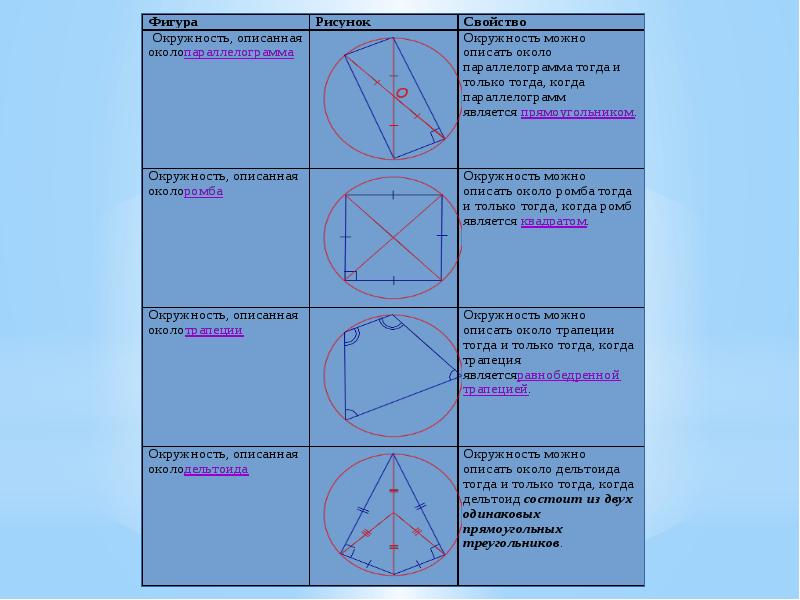
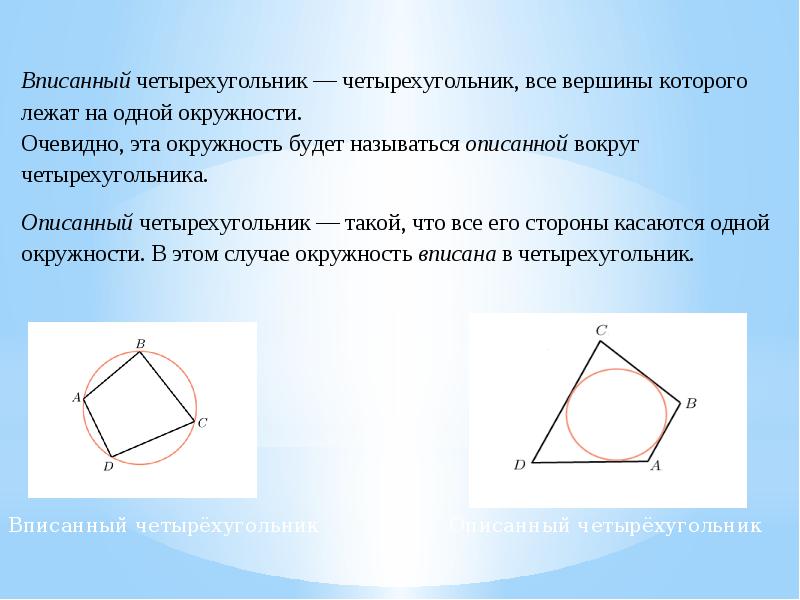
Вписанные четырёхугольники и их свойства       Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника .  В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность,  или  вписанным четырёхугольником.

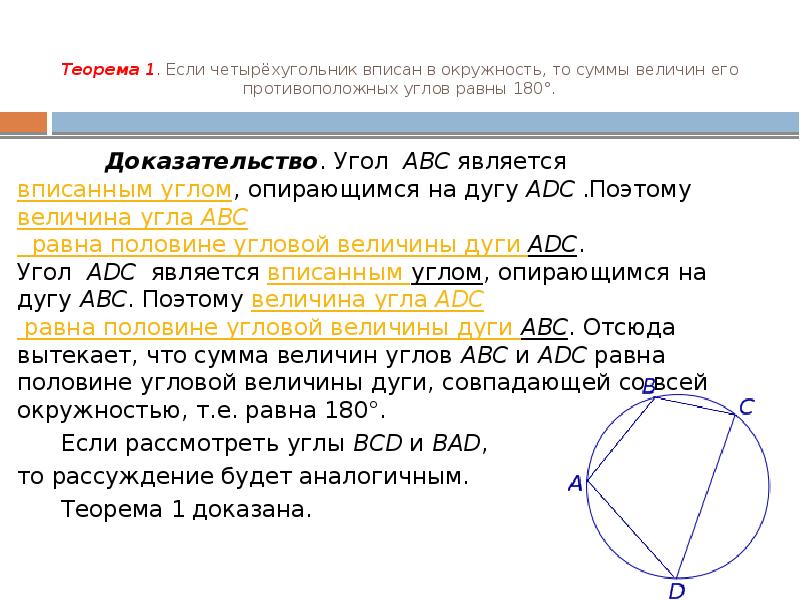
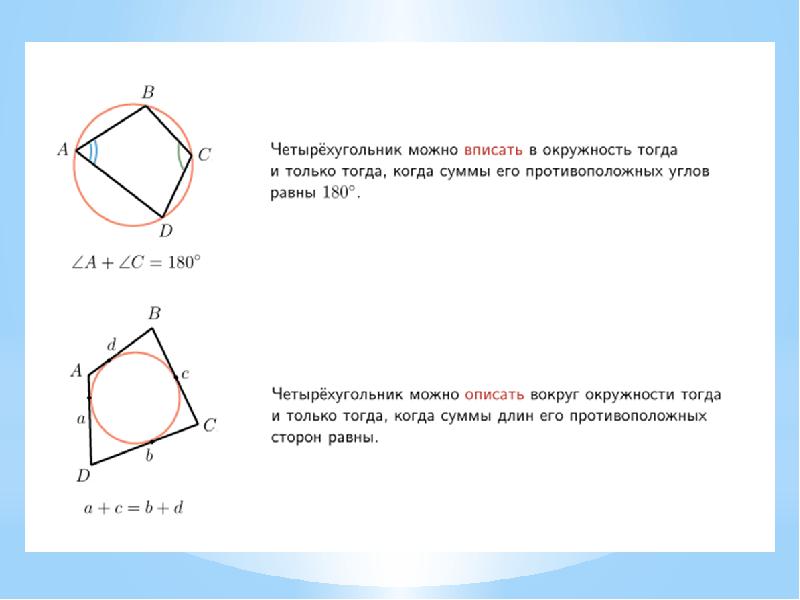
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.             Доказательство. Угол  ABC является вписанным углом, опирающимся на дугу ADC .Поэтому величина угла ABC  равна половине угловой величины дуги ADC. Угол  ADC  является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.       Если рассмотреть углы BCD и BAD, то рассуждение будет аналогичным.       Теорема 1 доказана.

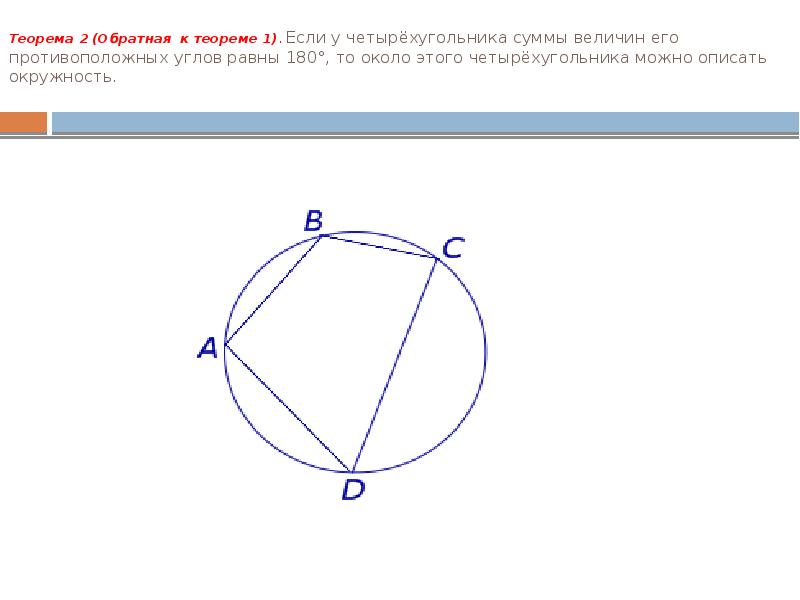
Теорема 2 (Обратная  к теореме 1). Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

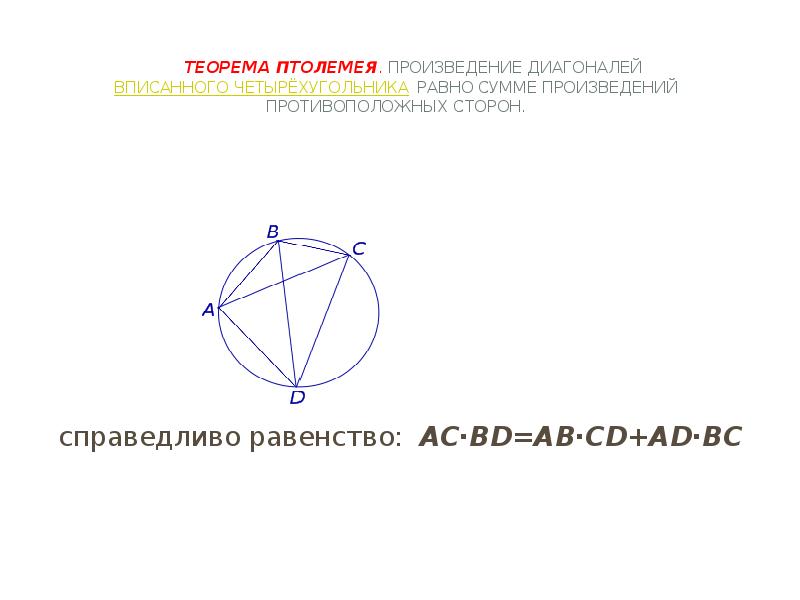
      Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.       справедливо равенство: AC∙BD=AB∙CD+AD∙BC

Выберем на диагонали AC точку E так, чтобы угол ABD  был равен углу CBE . Заметим, что треугольник ABD подобен треугольнику BCE. Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E), угол ADB  равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция: