Числа Каталана презентация

Исследовательская работа Выполнена учеником 11 класса «Б» муниципального образовательного учреждения «Общеобразовательная гимназия №3» г. Архангельска Руньковым Александром Александровичем   Научный руководитель: учитель математики ВКК муниципального образовательного учреждения «Общеобразовательная гимназия №3» г. Архангельска, Почетный работник общего образования РФ Косарева Галина Николаевна

Последовательность 1, 1, 2, 5, 14, 42, 132, 429, … в «Энциклопедии целочисленных последовательностей», созданной американским математиком и информатиком Нилом Джеймсом Александром Слоэном, имеет номер А000108 среди других пяти тысяч последовательностей. Последовательность 1, 1, 2, 5, 14, 42, 132, 429, … в «Энциклопедии целочисленных последовательностей», созданной американским математиком и информатиком Нилом Джеймсом Александром Слоэном, имеет номер А000108 среди других пяти тысяч последовательностей.

Введение

Цели и задачи

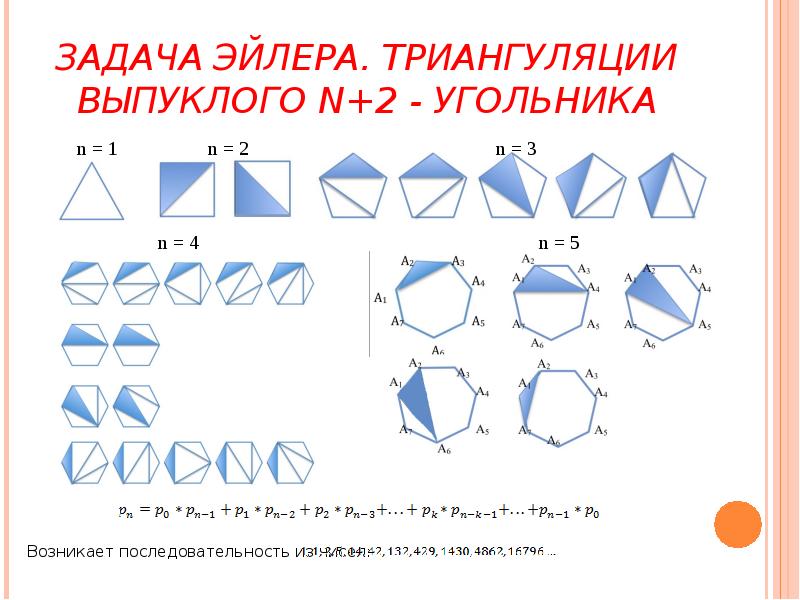
ЗАДАЧА ЭЙЛЕРА. ТРИАНГУЛЯЦИИ ВЫПУКЛОГО N+2 - УГОЛЬНИКА Иными словами, сколько существует различных способов разрезать выпуклый n+2 - угольник на треугольники непересекающимися внутри него диагоналями?

ЗАДАЧА ЭЙЛЕРА. ТРИАНГУЛЯЦИИ ВЫПУКЛОГО N+2 - УГОЛЬНИКА

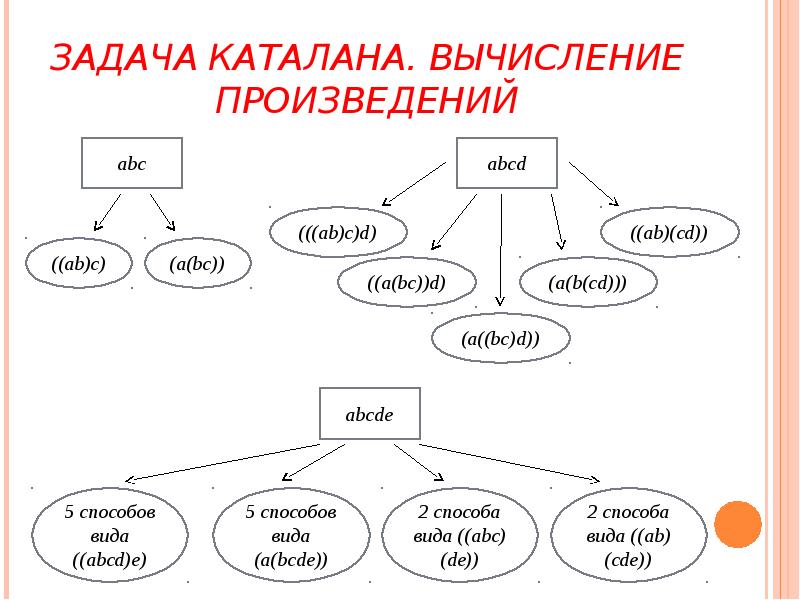
ЗАДАЧА КАТАЛАНА. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЙ Рассмотрим другую алгебраическую задачу. В строку записано произведение из букв. Требуется расставить пар круглых скобок так, чтобы внутри каждой пары скобок стояли либо две соседние буквы, либо буква и соседнее выражение в скобках, либо два соседних выражения в скобках. Например, . Найти количество различных перестановок скобок.

ЗАДАЧА КАТАЛАНА. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЙ

ЗАДАЧА КАТАЛАНА. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЙ Теперь выведем общую формулу для . Произведение в конечном счете получается как произведение произведения первых нескольких символов на некоторое произведение остальных: . Первые q символов могут быть скомбинированы способами, последние же n + 1 – q символов - способами. Таким образом, .

Итак, число различных перестановок пар скобок в произведении из n множителей, а также различных триангуляций выпуклого n+2-угольника задаётся следующим реккурентным соотношением: Итак, число различных перестановок пар скобок в произведении из n множителей, а также различных триангуляций выпуклого n+2-угольника задаётся следующим реккурентным соотношением:

СВЯЗЬ МЕЖДУ ЗАДАЧАМИ ЭЙЛЕРА И КАТАЛАНА Нельзя ли установить взаимно однозначное соответствие или, иначе говоря, биекцию между разбиениями на треугольники и способами подсчёта произведений? Оказывается, можно! Впервые это заметил математик Фордер в 1961 году.

СКОБОЧНЫЕ СТРУКТУРЫ В перестановке скобок из задачи Каталана уберём все буквы и две крайние скобки (самую левую и самую правую). То, что получится назовём правильной скобочной структурой. 1) Количество открывающих скобок равно количеству закрывающих; 2) Ни на каком начальном участке количество закрывающих скобок не превышает количество открывающих. К примеру, скобочные структуры ( ))( или ( )((( ))))( неправильные.

СКОБОЧНЫЕ СТРУКТУРЫ При n = 2 расстановок скобок две: ( )( ) и (( )). Пусть различных правильных скобочных структур из n пар скобок – . Сопоставим крайней левой скобке первую правую такую, что количества левых и правых скобок, заключённых между указанными скобками равны. Тогда между этими скобками заключена правильная скобочная структура из m пар скобок. Вне выбранных скобок расположена правильная скобочная структура из n – m – 1 пар скобок. В совокупности способов - . В силу произвольности выбора m из промежутка [0;n – 1] получаем уже знакомое нам реккурентное соотношение: .

Задачи, так или иначе приводящие к этому соотношению, иногда имеют явную связь между собой. Вместо того, чтобы искать громоздкое решение задачи и получать это соотношение снова и снова, можно установить взаимно однозначное соответствие с каким-нибудь уже известным комбинаторным объектом. Зачастую в качестве второго выступают именно правильные скобочные структуры. Задачи, так или иначе приводящие к этому соотношению, иногда имеют явную связь между собой. Вместо того, чтобы искать громоздкое решение задачи и получать это соотношение снова и снова, можно установить взаимно однозначное соответствие с каким-нибудь уже известным комбинаторным объектом. Зачастую в качестве второго выступают именно правильные скобочные структуры.

ТРЕУГОЛЬНИК КАТАЛАНА Со знаменитым треугольником Паскаля знаком каждый школьник. Но не каждый знает, что, если провести вертикальную черту, левее которой проходить нельзя и выписывать числа по правилу треугольника Паскаля, начиная с верхней единицы, на первых двух вертикалях возникают числа Каталана!

ПУТИ ДИКА И ЗАДАЧА ПРО КАРАНДАШИ «Имеются 12 карандашей попарно различной длины. Сколькими способами можно уложить их в коробку в 2 слоя по 6 карандашей так, чтобы в каждом слое карандаши были упорядочены по возрастанию длины (слева направо), а каждый карандаш верхнего слоя лежал строго над карандашом нижнего слоя и был короче его?»

ПУТИ ДИКА И ЗАДАЧА ПРО КАРАНДАШИ Если карандаш лежал в верхнем слое, то сопоставим ему движение вверх-вправо, а карандашу из нижнего слоя – движение вверх-влево. Так как карандашей в верхнем и нижнем слоях поровну (6), то верхний конец ломаной имеет координаты (0;12). На рисунке приведён пример такой ломаной.

ПУТИ ДИКА И ЗАДАЧА ПРО КАРАНДАШИ Таким образом, количество плохих ломаных однозначно определяется 5 движениями вверх-вправо и 7 движениями «вверх-влево», поэтому количество плохих ломаных равно . Количество хороших ломаных равно . В силу произвольности выбора начального общего количества карандашей для 2n получаем, что хороших укладок: . Нетрудно убедиться, что число различных путей Дика из 2n звеньев равно . Достаточно заметить, что путь Дика – это путь из верхней вершины треугольника Каталана до соответствующего числа на вертикальной черте. Отсюда следует, что .

ПЕРЕСТАНОВКИ ДОНАЛЬДА КНУТА «Сколькими способами можно так переставить n натуральных чисел, чтобы никакие три из чисел полученной последовательности не шли в порядке возрастания?»

ПЕРЕСТАНОВКИ ДОНАЛЬДА КНУТА Гипотеза

ПЕРЕСТАНОВКИ ДОНАЛЬДА КНУТА Правило №1

ПЕРЕСТАНОВКИ ДОНАЛЬДА КНУТА По правилу 1: При n = 1 очевидно: . Для n = 2 получаем две правильные скобочные структуры: и для перестановок 21 и 12 соответственно. Для n = 3 инъекция показана на рисунке.

ЧАСТНЫЕ СЛУЧАИ Как показано выше перестановкам 12 и 21 соответствуют структуры и . В зависимости от того на какое место вставляем 3 в перестановки 12 и 21 сопоставим ей пару скобок следующим образом: если 3 в перестановке стоит 1) на 1 месте, то сопоставляем ей крайнюю левую и крайнюю правую скобки

ЧАСТНЫЕ СЛУЧАИ 2) не на 1 месте, то сопоставляем ей подряд идущие закрывающую и открывающую скобки и вставляем их в соответствующую скобочную структуру непосредственно после открывающей скобки предыдущего числа

ЧАСТНЫЕ СЛУЧАИ Из полученных скобочных структур из трёх пар скобок получим расстановки скобок, которые сопоставим перестановкам Кнута из четырёх элементов, по тому же правилу, вставляя 4 в перестановки 321, 312, 231, 132 и 213. Если 4 в перестановке стоит 1) на 1 месте, то сопоставляем ей крайнюю левую и крайнюю правую скобки Если же после 4 в перестановке стоит не 3, то внутри пары уже поставленных скобок ставим соответствующую скобочную структуру, предварительно изменив её:

ЧАСТНЫЕ СЛУЧАИ а) перемещением закрывающей скобки из пары скобок, сопоставляемой первому числу, в место непосредственно перед первой встретившейся закрывающей скобкой в случае, если после этого первого числа идёт число, не меньшее его на 1 б) в случае, если после первого числа подряд идут числа, вместе с ним образующие в том же порядке убывающую арифметическую прогрессию с разностью 1, перемещением нескольких подряд идущих закрывающих скобок из пар скобок, сопоставляемых этим числам, в место непосредственно перед первой встретившейся закрывающей скобкой

ЧАСТНЫЕ СЛУЧАИ 2) не на 1 месте, то также сопоставляем ей подряд идущие закрывающую и открывающую скобки и вставляем их в соответствующую скобочную структуру непосредственно после открывающей скобки предыдущего числа

ЧАСТНЫЕ СЛУЧАИ

Правило №2 для общего случая Правило №2 для общего случая

Правило №2 для общего случая Правило №2 для общего случая

«Ответ от задачи не зависит!» «Ответ от задачи не зависит!»

Заключение Итак, числовая последовательность Каталана интересна прежде всего тем, что появляется очень часто, самым неожиданным образом во многих задачах из различных областей математики и преимущественно при решении комбинаторных проблем. В ходе исследования было дано несколько определений чисел Каталана различными способами, рассмотрены их взаимосвязи. Нами было подобрано, самостоятельно составлено и решено большое количество комбинаторных задач, в которых обнаруживаются числа Каталана и их свойства. Некоторые из задач приведены к общему случаю. В данной работе мы показали ряд свойств комбинаторных структур, связанных с числами Каталана, сформулировали правило для построении инъекции перестановок Дональда Кнута в правильные скобочные структуры для n. Таким образом, цель работы достигнута. Анализируя различные источники литературы, мы пришли к выводу, что числа Каталана актуальны и очень популярны в современной математике. Они часто встречаются на математических олимпиадах. Хочется отметить, что данная тема требует очень серьезного внимания и является не до конца изученной, несмотря на большое количество публикаций. Мы видим перспективы дальнейшего исследования в данной области в доказательстве достаточного условия биекции для перестановок Кнута при n, а также в выявлении новых комбинаторных объектов и их свойств, связанных с замечательной последовательностью Каталана.

Библиографический список 1. Виленкин Н. Я., Виленкин А. Н., Виленкин П. А. Комбинаторика. – М.: ФИМА, МЦНМО, 2010. – 400 с. 2. Гарднер М. Числа Каталана. // Квант. 1978. - №7. – с. 20-26. 3. Деза Е. И. Специальные числа натурального ряда: Учебное пособие. – М.: Книжный дом «ЛИБРОКОМ», 2011. – 240 с. 4. Спивак А. Числа Каталана. // Квант. 2004. - №3. – с. 2-10. 5. Попов И. Н. Совершенные и дружественные числа: Учебное пособие. – Архангельск: Поморский университет, 2005. – 153 с. 6. Прасолов В. В. Задачи по алгебре, арифметике и анализу: Учебное пособие. - М.: МЦНМО, 2007. – 608 с. 7. Энциклопедия для детей. Т. 11. Математика/ Гл. ред. М. Аксенова. – М.: Аванта +, 2007. – 688 с. 8. Электронная энциклопедия «Большая энциклопедия Кирилла и Мефодия 2007». 9. http://www.mk.ru/msu/ - официальный сайт олимпиады МГУ «Покори Воробьёвы горы» (дата посещения - 02.12.2011). 10. http://mat.1september.ru/ - Издательский дом «Первое сентября». Учебно-методическая газета «Математика» (дата посещения - 23.12.2011). 11. http://www.research.com/ - «Он-лайн энциклопедия целочисленных последовательностей» Н. Д. А. Слоэн (дата посещения - 11.11.2011). 12. http://ru.wikipedia.org/ - Свободная энциклопедия «Википедия» (дата посещения - 21.01.2012).

Спасибо за внимание!