Диаметр, радиус и центр графа презентация

Диаметр, радиус и центр графа

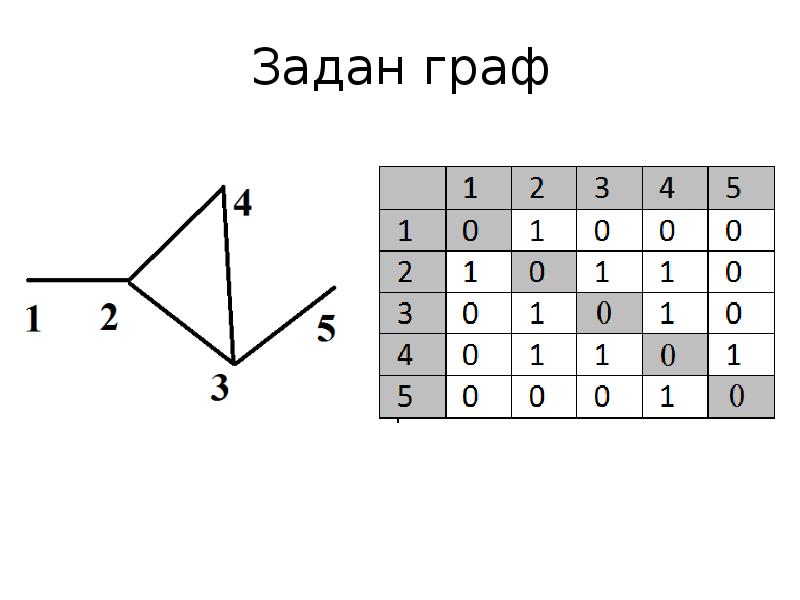
Задан граф

Ввод данных int main() { int G[100][100], // граф транспортной сети R[100][100], // минимальные расстояния // между вершинами I,j,n, // n – число вершин cin >> n; for (i=1; i<=n; i++) for (j=1; j<=n; j++) cin >> G[i][j];

Oпределение длины кратчайших путей int r[100]={0}, // 0 – расстояние не определено ob[100], // обработанные вершины For (n_p=1; n_p<n; n_p++) { Int a=1, // вершина из ob , которая обрабатывается p=2; // пустое место для записи новых вершин r[n_p]=1; // кратчайший путь в n_p – 1 ob[1]=n_p; // while a<p do { for (i=0; i<n; i++) // ищем связанные с ob[a] if (G[i][ob[a]]==1 & r[i]==0) { //необработанные вершины r[i]=r[ob[a]]+1; ob[++p]=I; } a++; } for(i=1; i<=n; i++) R(n_p][i]=r[i]; }

Определение.  Диаметр связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим матрицу кратчайших расстояний между вершинами

Определение диаметра графа int D=0; For(i=1; i<=n; i++) For(i=1; i<=n; i++) D:= max(D,R[i][j]); Cout << “Диаметр графа = “ << D;

Определение.  Радиус связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим матрицу кратчайших расстояний между вершинами

Определение радиуса графа int Rad=0; for(i=1; i<=n; i++) { int M=0; for(i=1; i<=n; i++) M:= max(M,R[i][j]); if (i==1) Rad=M; else Rad=min(Rad,M); } cout << “Радиус графа = “ << Rad;

Определение.  Центр графа – вершина, максимальное расстояние от которого до любой другой вершины является наименьшим из всех возможных. Для решения задачи строим матрицу кратчайших расстояний между вершинами

Определение центра графа // Rad – радиус графа for(i=1; i<=n; i++) { int M=0; for(i=1; i<=n; i++) M:= max(M,R[i][j]); if (Rad==M cout << “Центр графа = “ << i; }