ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ презентация
Содержание
- 2. Магнитная энергия тока Замкнем цепь, содержащую R и L на
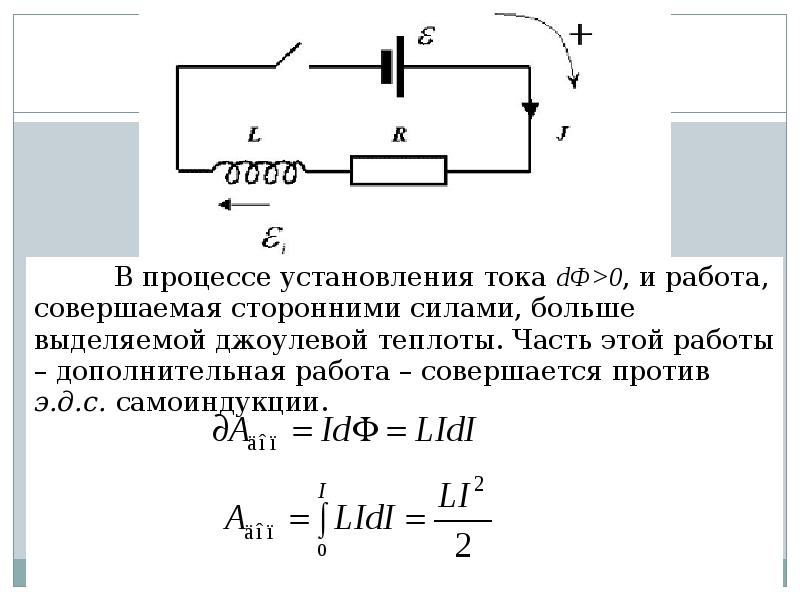
- 3. В процессе установления тока dФ>0, и работа, совершаемая сторонними силами, больше
- 4. По закону сохранения энергии любая работа идет на приращение какого-то вида
- 5. Энергия магнитного поля Полученную формулу преобразуем, введя в нее характеристику
- 6. Эта формула справедлива для однородного поля, заполняющего объем V. Таким образом
- 7. Существует другая возможность расчета индуктивности из выражения энергии:
- 8. Магнитная энергия двух контуров с токами Возьмем два неподвижных контура
- 9. Найдем эту работу за время dt: Учтем, что:
- 10. После подстановки будем иметь После подстановки будем иметь Учтем, что:
- 11. Вычислим энергию двух контуров несколько иначе – с точки зрения локализации
- 12. Формулы (1) и (2) приводят к таким важным следствиям: 1. Магнитная
- 13. 4. Сопоставление выражений (1) и (2) показывает, что:
- 14. Энергия и силы в магнитном поле Наиболее общий метод определения
- 15. Согласно закону сохранения энергии работа , которую совершает источник
- 16. Эта работа, которую мы называем дополнительной, равна: учтем, что для каждого
- 17. Именно эта часть работы идет на приращение магнитной энергии системы и
- 18. Если
- 19. Половина дополнительной работы идет на приращение магнитной энергии системы, а другая
- 20. Скачать презентацию


















Слайды и текст этой презентации
Похожие презентации





























