ГИДРОЦИКЛОНИРОВАНИЕ презентация
Содержание
- 2. Основная литература: Основная литература: Фролов Ю. Г. Курс коллоидной химии. Поверхностные
- 3. ЛЕКЦИЯ 1. Выбор оборудования и материалов для разделения дисперсных систем.
- 4. Требования к конечному продукту и шламу Требования к конечному продукту и
- 5. Внимание!!! Для однозначного определения и фиксации всех факторов, составление развернутого ТЗ
- 6. Выбор процесса разделения дисперсной системы: осаждение, фильтрование, центробежная очистка (фильтрование и/или
- 7. Проведение экспериментов на лабораторных установках, моделирующих работу промышленного оборудования. Основная цель
- 8. Оценка экспериментально-расчетным методом ресурсных характеристик, включая снижение расчетных параметров. Оценка экспериментально-расчетным
- 9. Опытно-промышленная проверка выбранных или разработанных единиц оборудования. Опытно-промышленная проверка выбранных
- 11. Лекция 2. Основные виды классификаций свободнодисперсных систем F=K-Ф+2 и F=K-Ф+3 F – число
- 12. Основные классификации фазового состояния и дисперсности систем Общая классификация дисперсных систем
- 13. Основные классификации фазового состояния и дисперсности систем Детальная классификация дисперсных систем
- 14. Классификация дисперсных систем в гидросфере Классификация дисперсных систем в гидросфере С
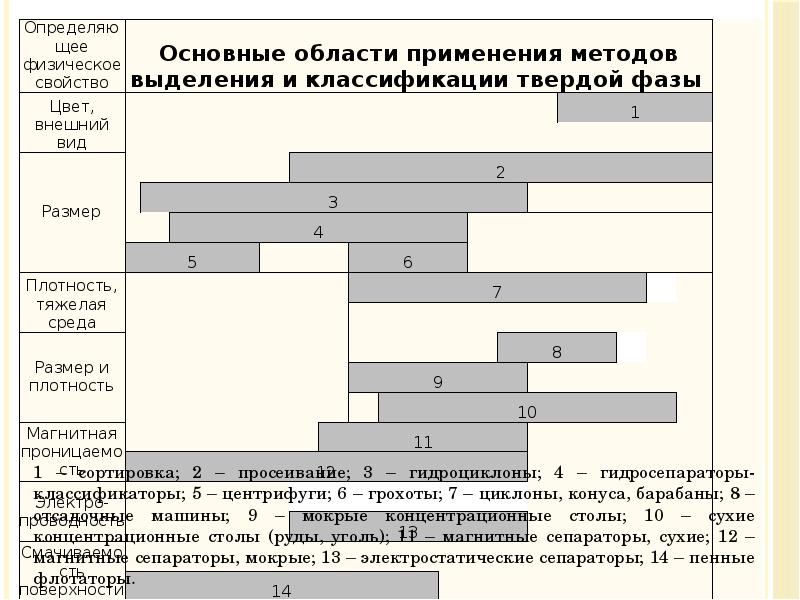
- 15. Классификация методов очистки загрязненных вод
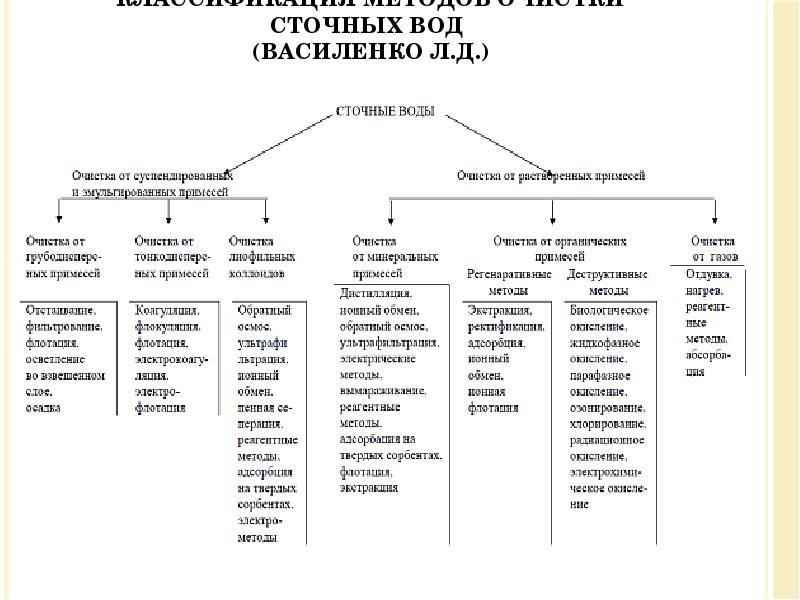
- 16. Классификация методов очистки сточных вод (Василенко Л.Д.)
- 18. Лекция 3. Теоретические основы разделения дисперсных систем Седиментация
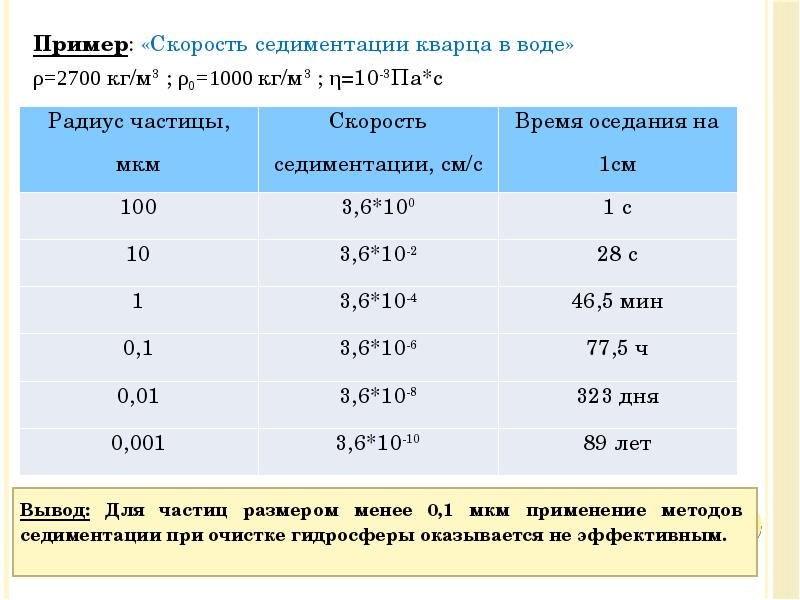
- 19. При ламинарном движении частиц: При ламинарном движении частиц: Для стоксовской частицы:
- 20. Пример: «Скорость седиментации кварца в воде» Пример: «Скорость седиментации кварца в
- 21. Условие седиметационно-диффузионного равновесия Внимание! Единичная частица всегда осядет! Учет диффузии необходим
- 22. Замечание: С увеличением размера частиц быстро растет поток седиментации ic ≈
- 23. Пусть iD = ic - условие седиментационно-диффузионного равновесия. Исходя из опыта
- 24. Замечание: Если сравнить седиментацию при наличии диффузии и без нее, то
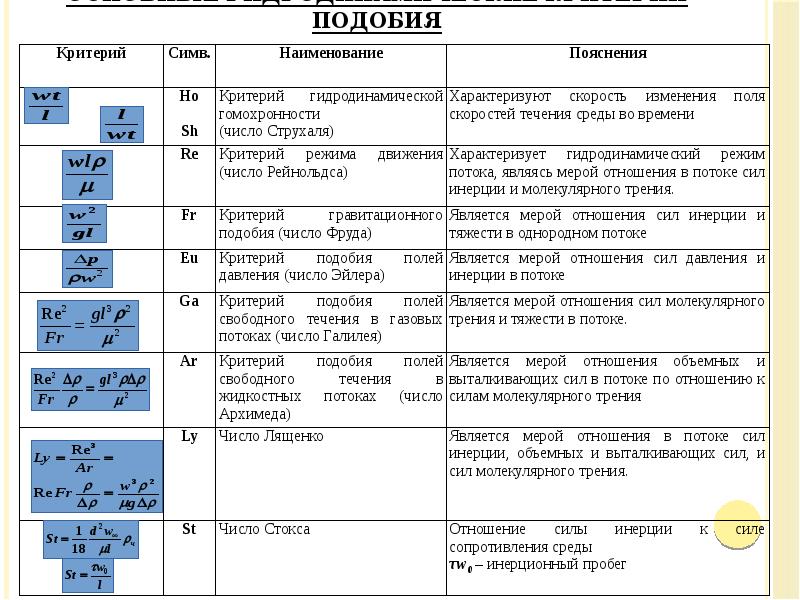
- 25. Основные гидродинамические критерии подобия
- 26. Применение закона Ньютона-Риттенгера Закон Ньютона-Риттенгера:
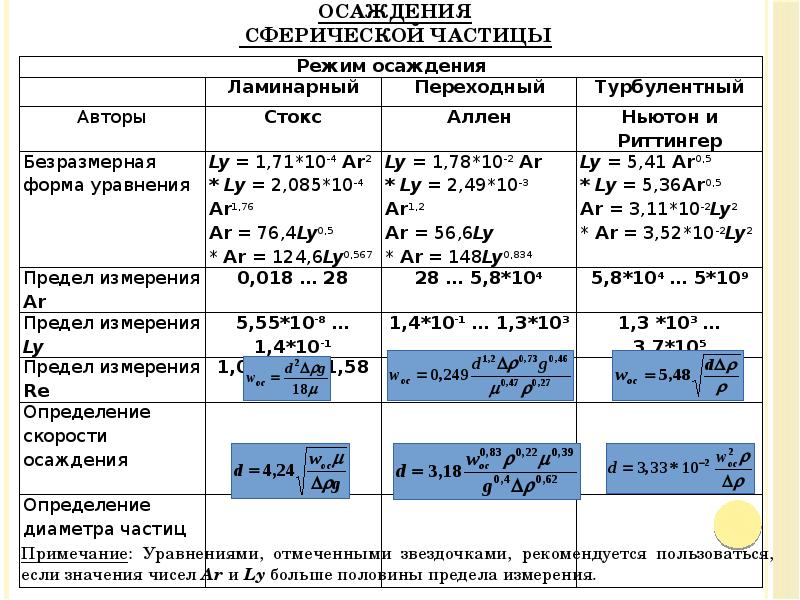
- 27. Уравнения для расчета процесса свободного осаждения сферической частицы Примечание: Уравнениями, отмеченными
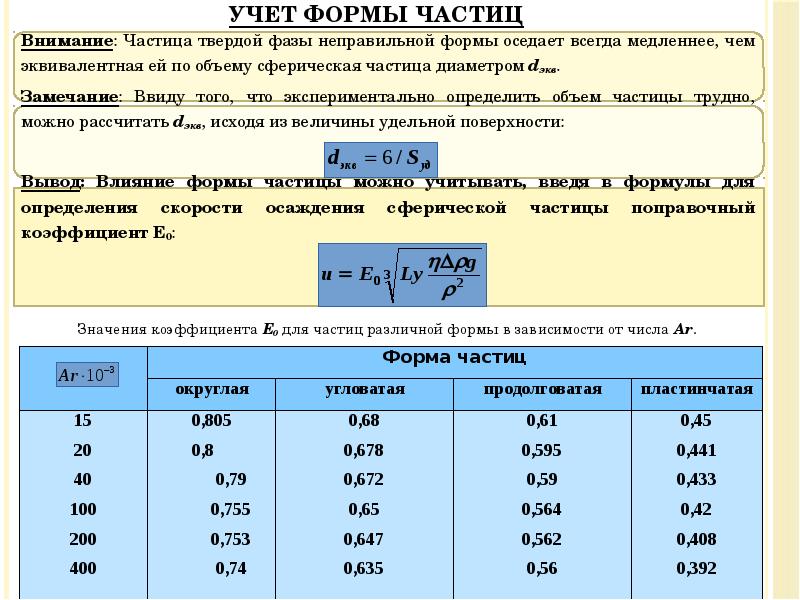
- 28. Учет формы частиц Внимание: Частица твердой фазы неправильной формы оседает всегда
- 29. Учет стесненного осаждения Замечание: При увеличении содержания твердой фазы в суспензии
- 30. Лекция 4. Теоретические основы разделения дисперсных систем. Движение по окружности. Центрифугирование
- 31. Движение частиц по окружности Используя закон Ньютона-Риттенгера, получаем: Для ламинарного, турбулентного
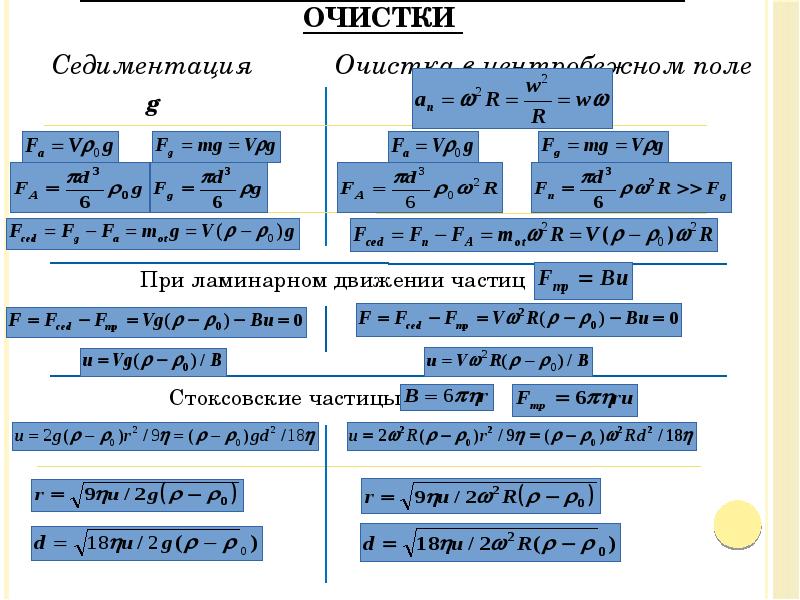
- 32. Расчетные зависимости методов очистки Седиментация g
- 33. Особенности движения частиц по окружности Пример: Определить предельные диаметры частиц d1
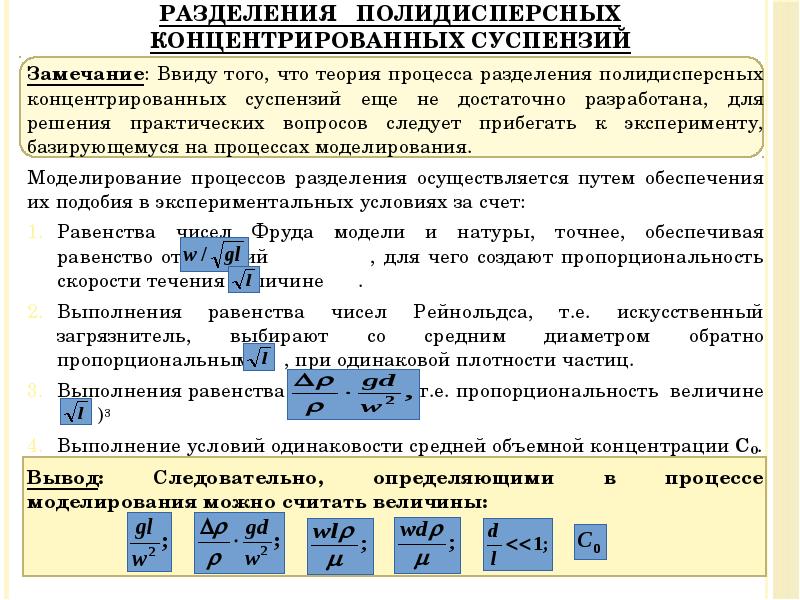
- 34. Замечание: Ввиду того, что теория процесса разделения полидисперсных концентрированных суспензий еще
- 35. Центрифугирование Справочно: Центрифугирование – разделение неоднородных систем (напр., жидкость – твердое
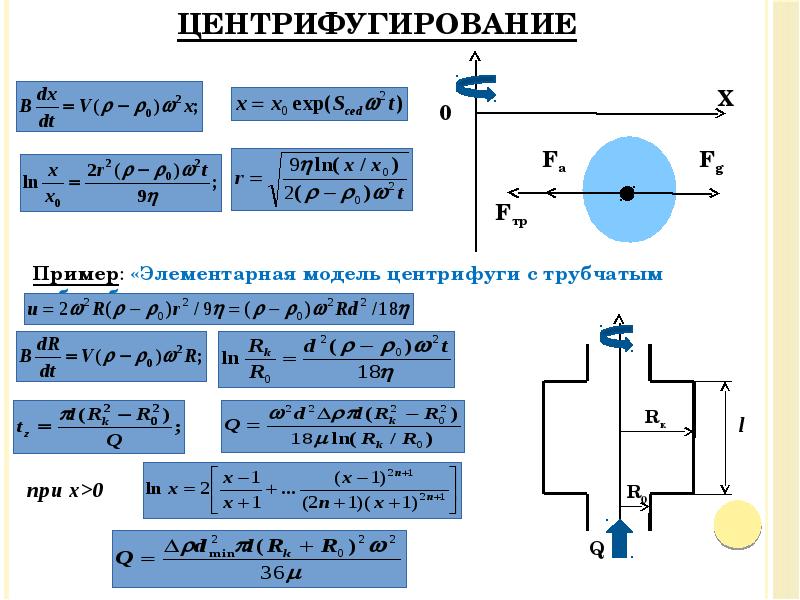
- 36. Пример: «Элементарная модель центрифуги с трубчатым барабаном» Пример: «Элементарная модель
- 37. Основные преимущества центрифуг по сравнению с механическими фильтрами: Основные преимущества центрифуг
- 38. Внимание! Многие, но далеко не все, недостатки центрифуг могут быть скомпенсированы
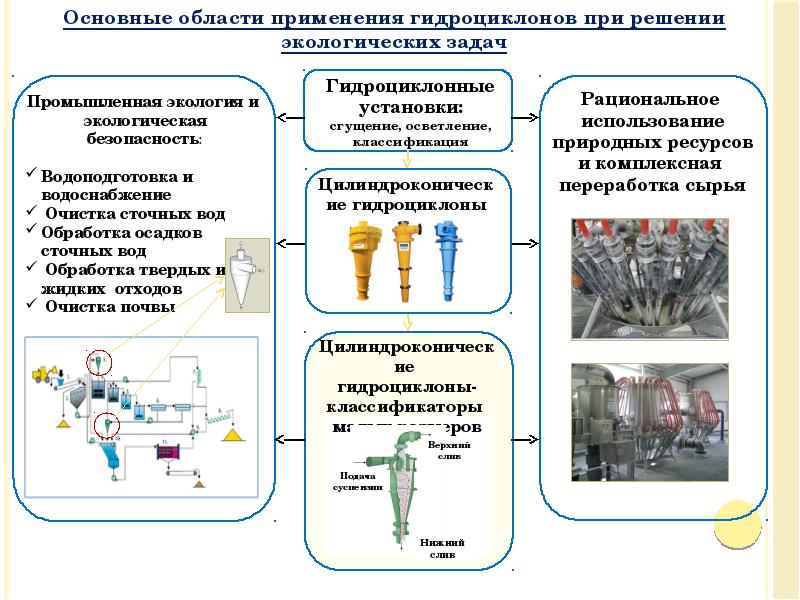
- 39. Лекция 5. Гидроциклонирование Справочно: Гидроциклонирование - разделение неоднородных систем (напр., жидкость
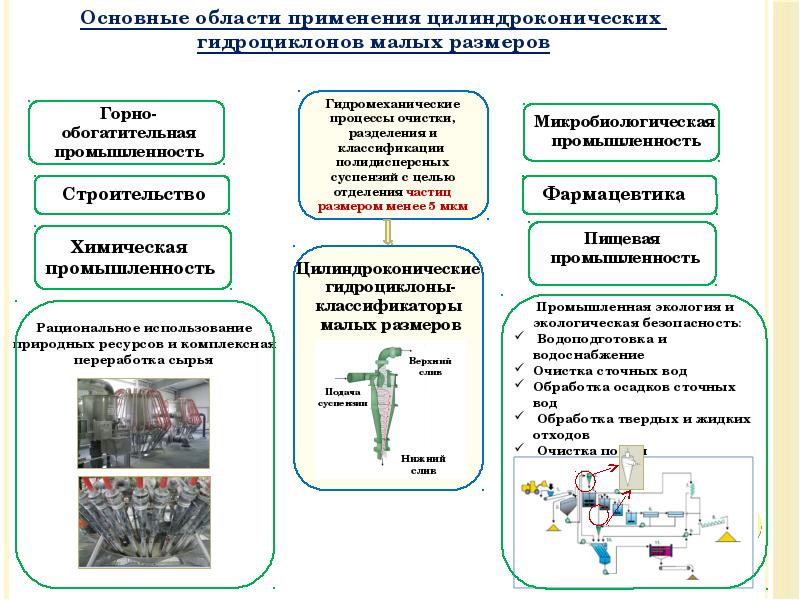
- 40. Основные группы гидроциклонов Замечание: Аппараты первых двух групп имеют свои специфические
- 41. Основные типы конструкций гидроциклонов турбоциклоны; Замечание: Использование турбоциклонов в промышленной
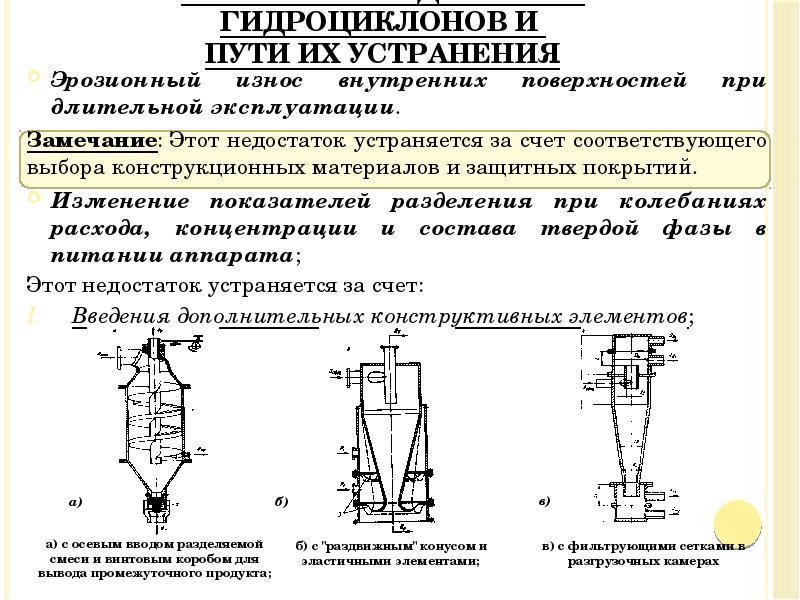
- 42. Основные недостатки гидроциклонов и пути их устранения Эрозионный износ внутренних поверхностей
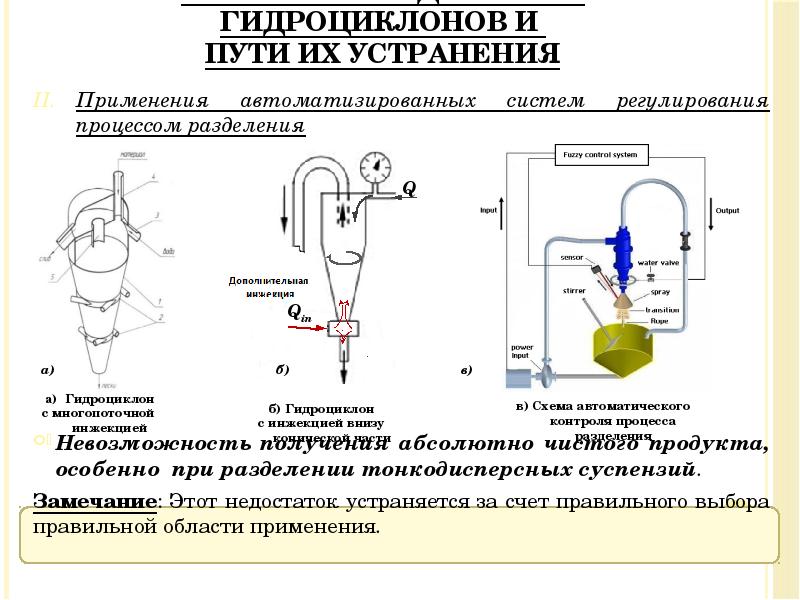
- 43. Применения автоматизированных систем регулирования процессом разделения Применения автоматизированных систем регулирования процессом
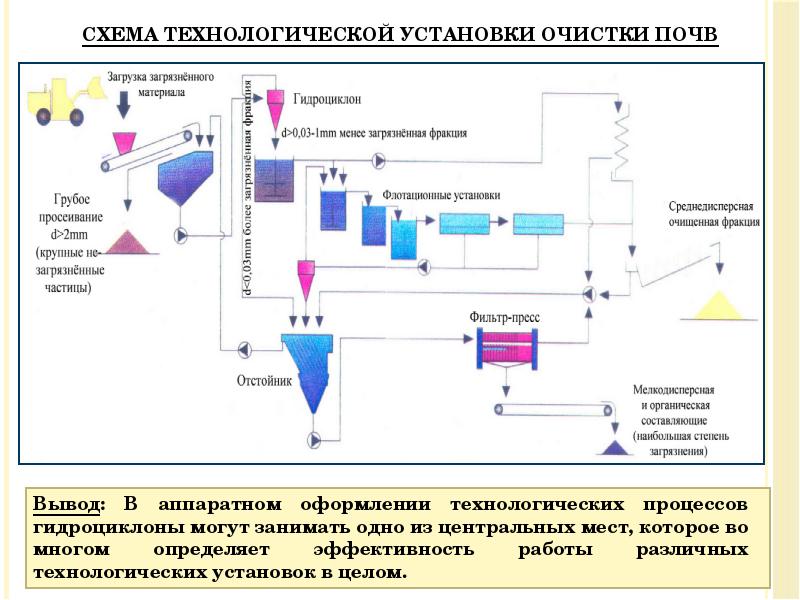
- 46. Схема технологической установки очистки почв Вывод: В аппаратном оформлении технологических процессов
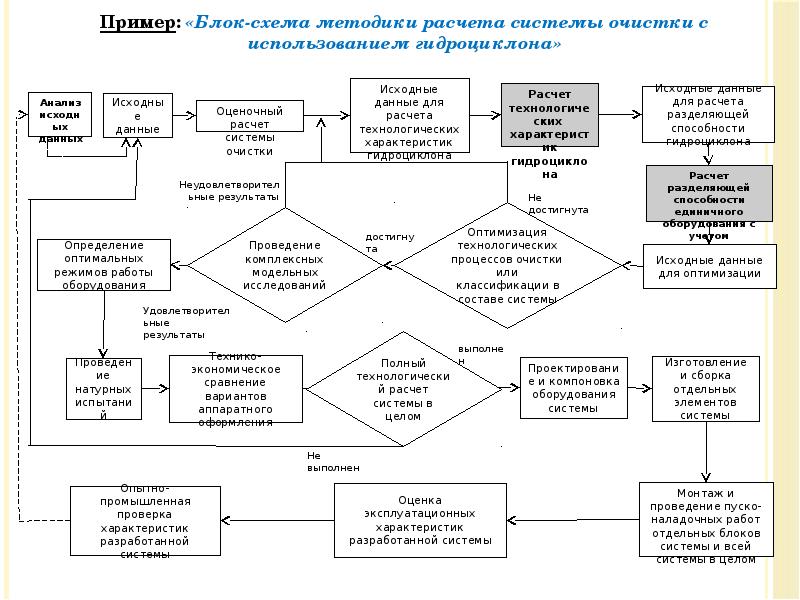
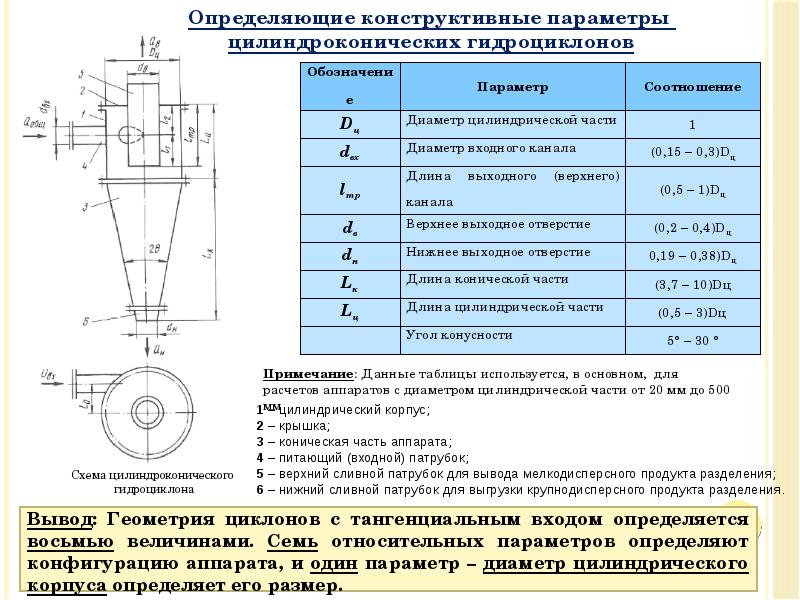
- 47. Лекция 6. Методы расчета гидроциклонов Принято выделять следующие методы расчета гидроциклонов:
- 49. Внимание! Можно выбрать и другие варианты геометрии, но при этом следует
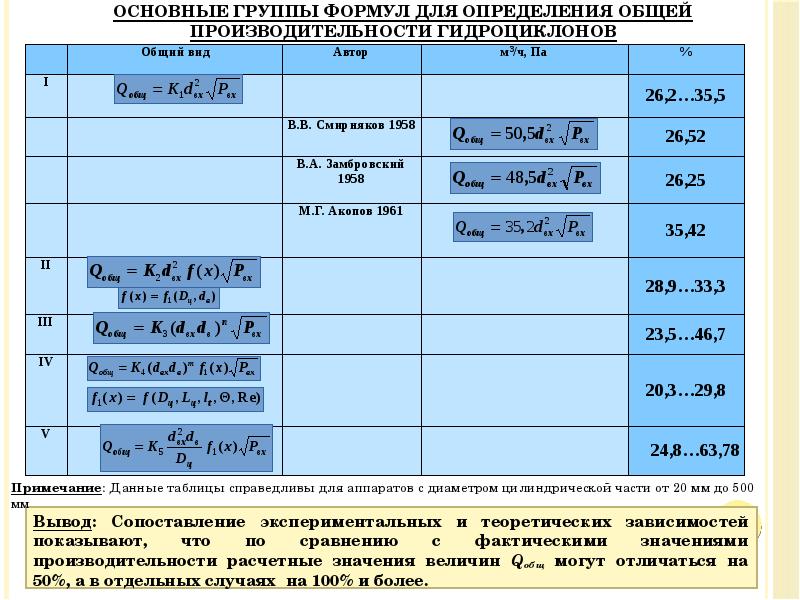
- 50. Общая производительность гидроциклонов Можно выделить несколько основных расчетных схем при выводе
- 51. Вывод: Сопоставление экспериментальных и теоретических зависимостей показывают, что по сравнению с
- 52. Методика расчета основных размеров гидроциклона Внимание! Если размеры гидроциклона не
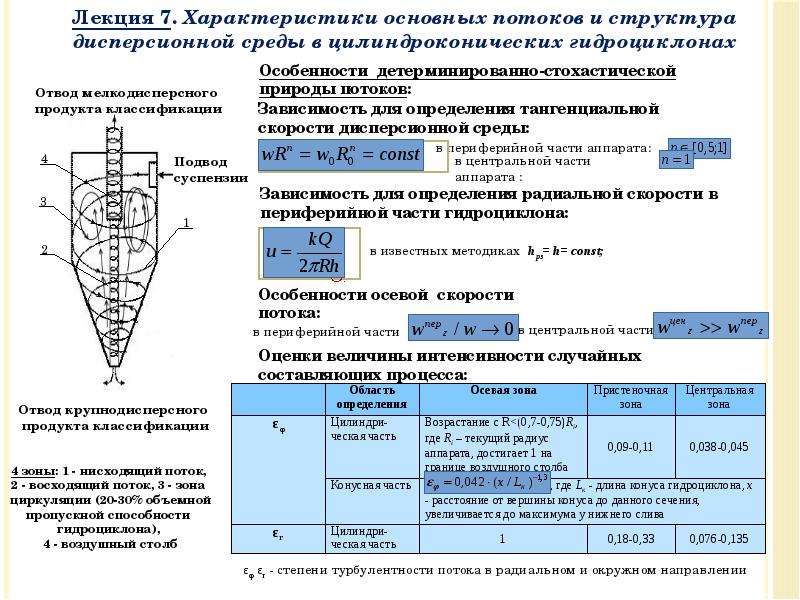
- 54. Уравнение движения Теорема Кориолиса определяет силы инерции и описывает движение
- 55. Уравнение движения В первой скобке
- 56. Если рассматривать криволинейное движение стоксовской сферической частицы массы mч и диаметра
- 57. Первый член уравнения связан с ускорением классификационного движения и может быть
- 58. В результате для радиального движения частиц получаем: В результате для радиального
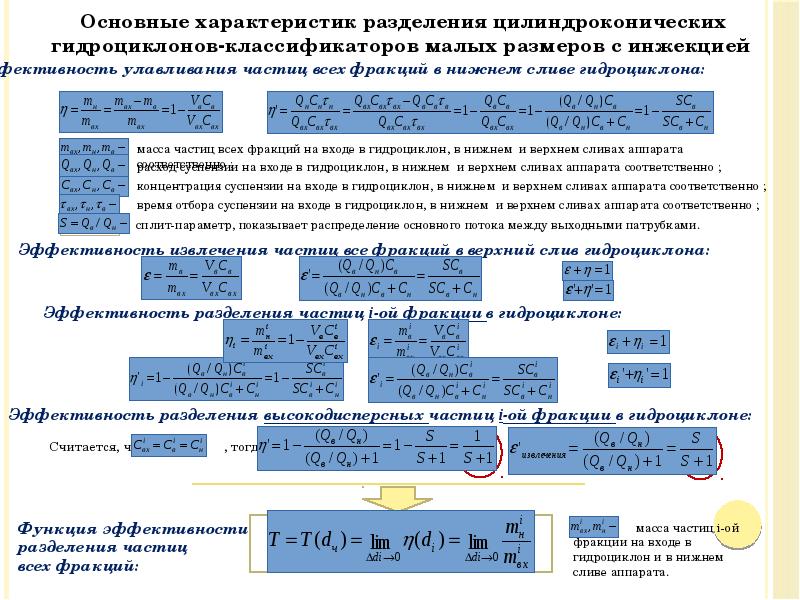
- 59. Существует три основных определения понятия граничного зерна: Существует три основных определения
- 62. Тогда функция: Тогда функция: f ({R},{δ}, t) d{δ}d{R} = fп ({R},{δ},
- 63. По определению условной плотности распределения одной из случайных величин, входящих в
- 64. Для описания изменения гранулометрического состава примесей нас в большей мере будет
- 65. Для нахождения кинетического уравнения функции fΣ (δ, t) введем в рассмотрение
- 66. Если принять ln fсΣ (δ) = const - kU(δ), то выражение
- 67. Тогда кинетическое уравнение (1.15) для функции fΣ (δ, t), полученное исходя
- 68. При этом, используя принцип максимума энтропии и считая, равновесные и стационарные
- 69. Соответственно имеем: Соответственно имеем: n0 (Rδ0, t) = n0 (Rδ0, t)
- 70. В уравнении (1.21) величина n0 ф (Rδ0, t) wпф(R) отлична от
- 71. Уравнения (1.15) и (1.22) при наличии граничных и начальных условий могут
- 72. Скачать презентацию




















































Слайды и текст этой презентации
Похожие презентации





























