Конус. Понятие конуса. Площадь поверхности конуса. Усеченный конус
Содержание
- 4. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его
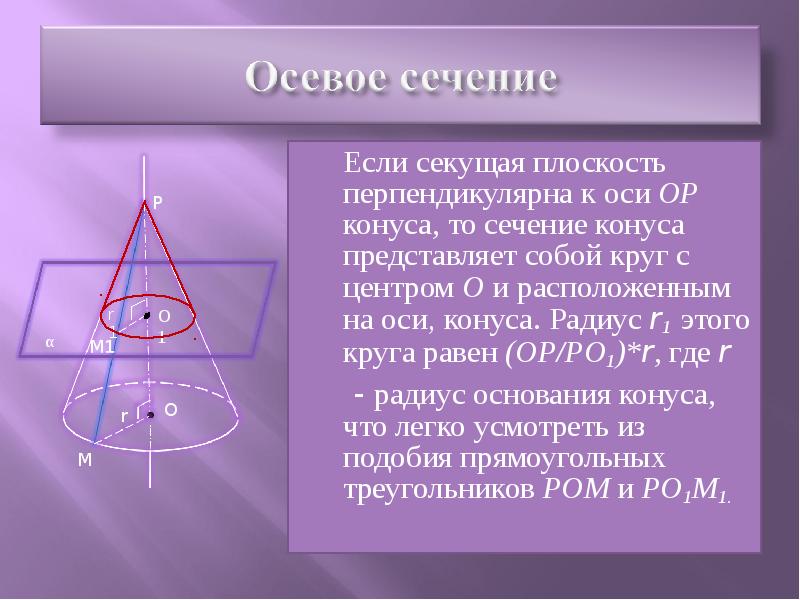
- 6. Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса
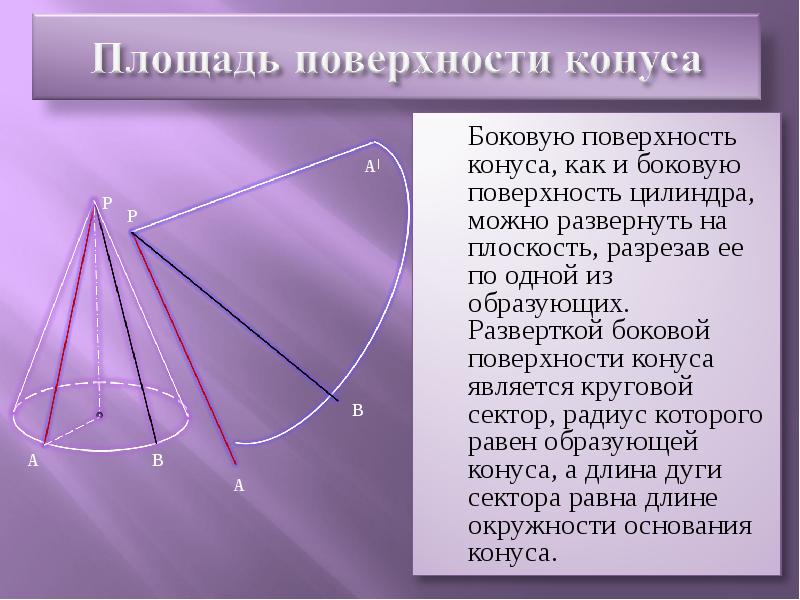
- 8. За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь
- 9. Sбок =
- 11. Подставив это выражение в формулу (1), получим Подставив это выражение в
- 12. Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности
- 23. Скачать презентацию



















Слайды и текст этой презентации
Презентация на тему Конус. Понятие конуса. Площадь поверхности конуса. Усеченный конус доступна для скачивания ниже:
Похожие презентации