Лекция 3 1. Линейный интеграл в векторном поле, его свойства. Работа силового презентация
Содержание
- 2. § 1. Линейный интеграл в векторном поле. Циркуляция векторного поля.
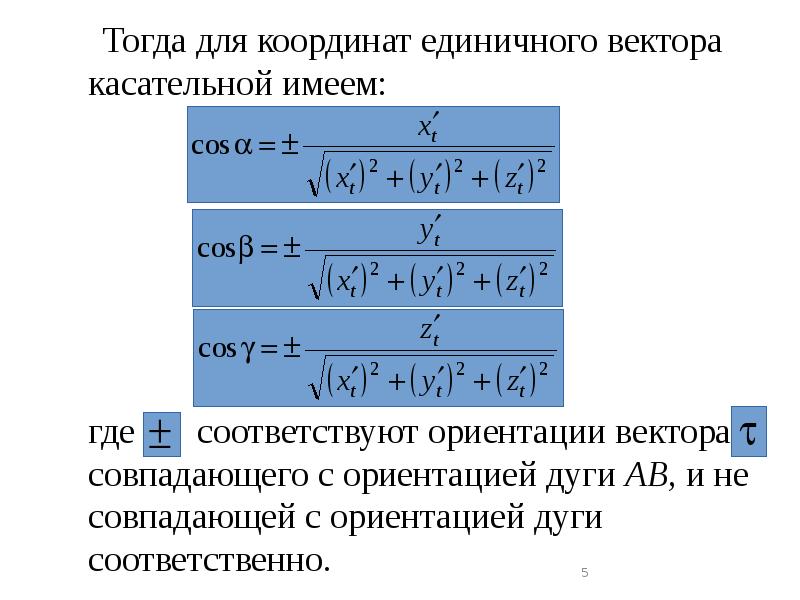
- 4. - углы которые составляет вектор с осями координат. Считаем, что дуга
- 5. Тогда для координат единичного вектора касательной имеем: Тогда для
- 6. Длина элемента дуги может быть найдена по формуле Рассмотрим в каждой
- 7. Этот интеграл называется линейным интегралом в векторном поле. Этот
- 8. Чтобы найти полную работу, необходимо проинтегрировать по всей длине дуги AB:
- 9. то значение этого интеграла называется циркуляцией векторного поля и обозначается буквой
- 10. § 2. Теорема Стокса. Если в 3-х мерном пространстве функции
- 11. 3) Задана гладкая ориентированная поверхность S, натянутая на контур такая что,
- 12. Формула, связывающая криволинейный интеграл по замкнутому контуру натянутая на поверхность S
- 13. § 3. Ротор векторного поля. Векторная запись теоремы Стокса. Пусть
- 14. Найдем работу, которую Найдем работу, которую совершает векторное поле
- 15. Учитывая связь между поверхностными интегралами 2-го и 1-го рода имеем:
- 16. и единичного вектора нормали к поверхности Таким образом,
- 17. Вектор характеризует вращательную способность поля. Если он равен 0, то
- 18. Векторная запись теоремы Стокса Теорема Стокса связывает:
- 19. Это векторная запись теоремы Стокса. Смысл: Циркуляция векторного поля равна
- 20. § 4. Плотность циркуляции, связь её с ротором. Пусть в векторном
- 21. Если циркуляцию разделим на площадь контура ℓ, то получим число, характеризующее
- 22. Определение. (плотности циркуляции) Плотностью циркуляции в точке М по направлению
- 23. § 5. Вычисление циркуляции. § 5. Вычисление циркуляции. Ее можно вычислить
- 24. Определение. Векторное поле называется потенциальным, в некоторой односвязанной области V,
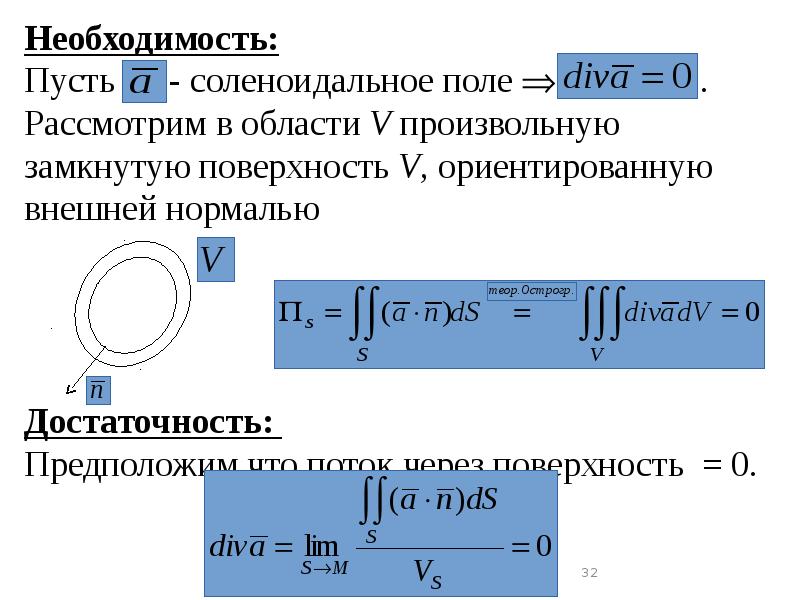
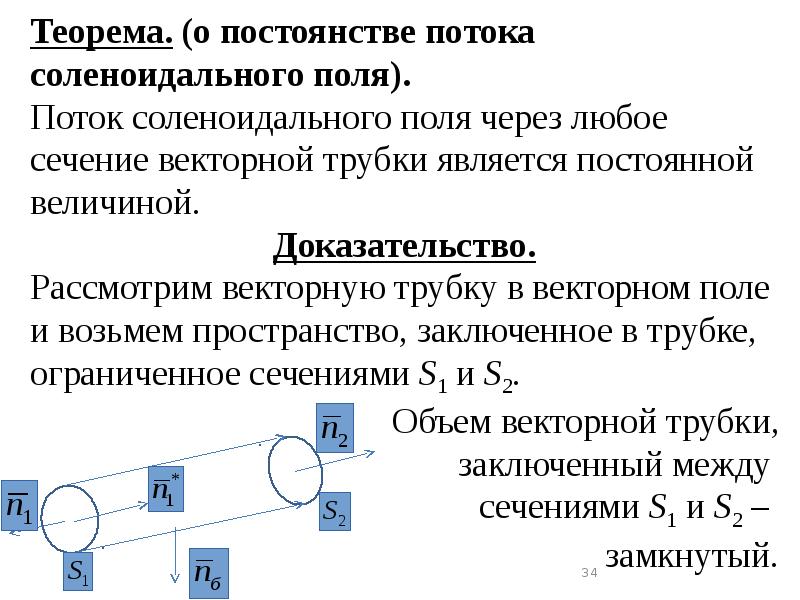
- 34. Теорема. (о постоянстве потока соленоидального поля). Теорема. (о постоянстве потока соленоидального
- 35. Поверхность, ограничивающая объем состоит из 3-х поверхностей , и
- 47. Скачать презентацию











































Слайды и текст этой презентации
Скачать презентацию на тему Лекция 3 1. Линейный интеграл в векторном поле, его свойства. Работа силового можно ниже:
Похожие презентации





























