Метод рационализации при решении показательных и логарифмических неравенств презентация

Метод рационализации при решении показательных и логарифмических неравенств  

Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные выражения к равносильному ему рациональному неравенству. Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные выражения к равносильному ему рациональному неравенству. Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени. Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)

  Таблица работает при условии :f›0,g›0,h›0,h≠1 где f и g— функции от х, h— функция или число, V— один из знаков ≤,›,≥,‹ Заметим также, вторая и третья строчки таблицы — следствия первой.

И еще несколько полезных следствий : И еще несколько полезных следствий : где f и g — функции от x, h— функция или число, V— один из знаков ‹,≥,≤,›

Пример 1: Пример 1:

Пример 2: Пример 2:

Задание для решения с доской:

Рассмотрим таблицы, позволяющие рационализировать показательный неравенства . Рассмотрим таблицы, позволяющие рационализировать показательный неравенства . Таблица для рационализации в показательных неравенствах: f и g— функции от x, h— функция или число, V— один из знаков ›,≤,≥,‹.Таблица работает при условии  h›0,h≠1. Опять же, по сути, нужно запомнить первую  и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка — частный случай третьей.  

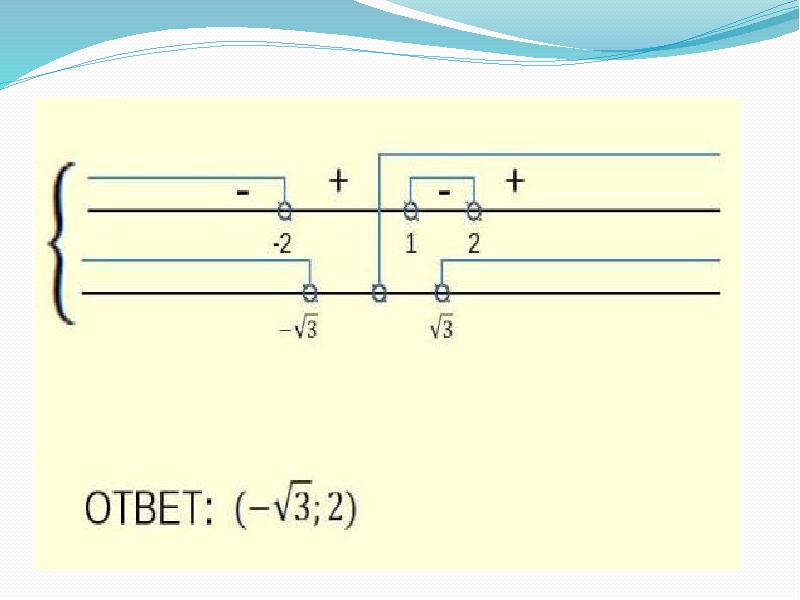
Пример: Пример: (x2-x-2)2x-6 ≥ (x2-x-2)3-4x X2-x-2›0 х2-x-2 ≠1 ((X2-x-2)-1)((2x-6)-(3-4x))≥ 0   x›2 x‹-1 (x2-x-3)(6x-9)≥0 , , ,x2= , x3=1,5

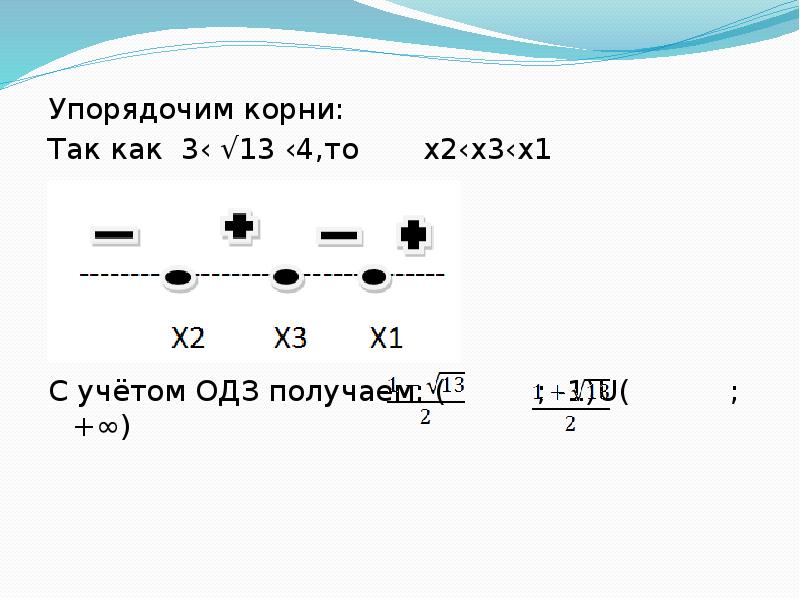
Упорядочим корни: Упорядочим корни: Так как 3‹ √­­­13 ‹4,то x2‹x3‹x1 С учётом ОДЗ получаем: ( ; -1)U( ; +∞)

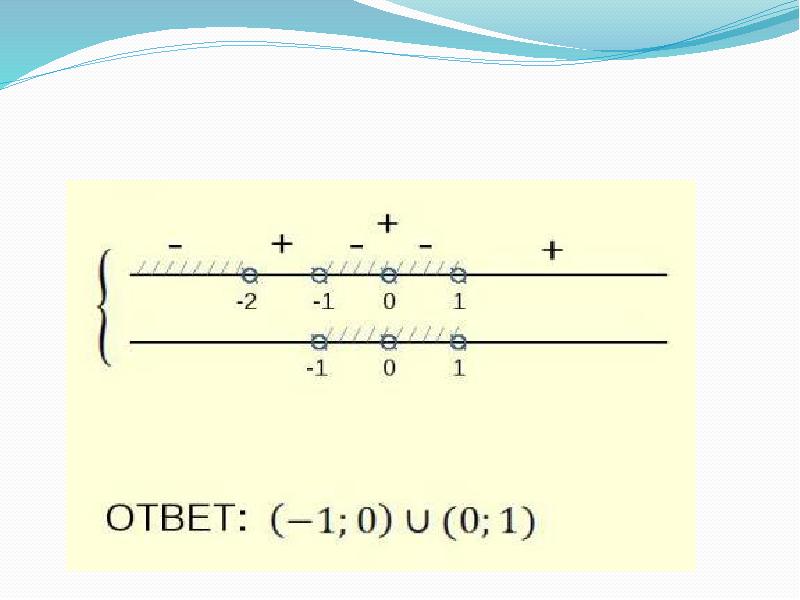
Устное упражнение: назвать чему равносильно данное неравенство без учёта ОДЗ 1.logx-3(x2+3x-4)≤ logx-3(5-x) 2.(x-3)x-4 ≤ Далее рассмотрим пример решения системы неравенств:

Решение. Решение. 1.Решим первое неравенство: 2. Решим второе неравенство при всех х При условиях и получаем неравенство При указанных условиях получаем: 3. Решением системы является общая часть решений двух неравенств.  

Так как имеем откуда получаем решение системы. Ответ: