Методы поиска условного экстремума презентация

Методы поиска условного экстремума Выполнил: Шеломенцев Владислав ИХПБДиТБ 1 курс маг.

УСЛОВНЫЙ ЭКСТРЕМУМ Точка (х0,у0) называется точкой условного экстремума (максимума или минимума), если существует такая окрестность этой точки, что для всех точек (х,у) из этой окрестности, удовлетворяющих условию g(x,y)=C, выполняется неравенство: max min

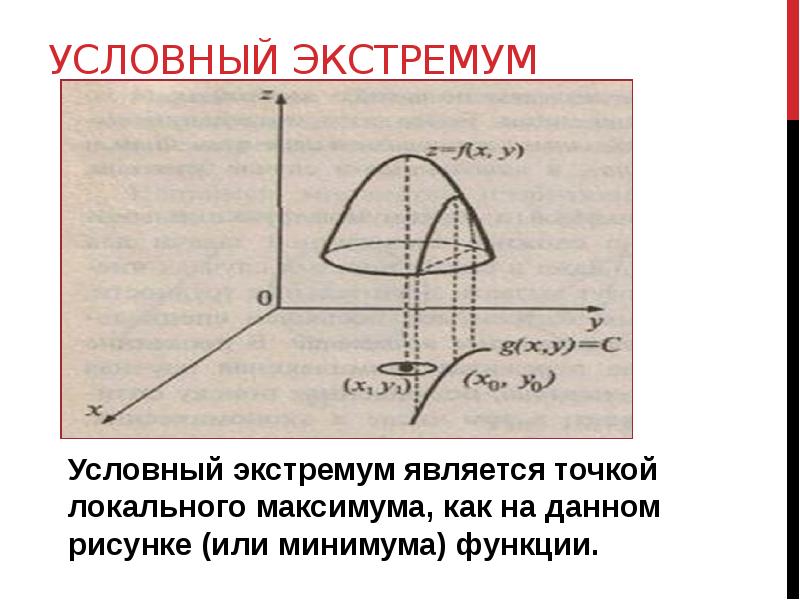
УСЛОВНЫЙ ЭКСТРЕМУМ

УСЛОВНЫЙ ЭКСТРЕМУМ Существует два основных метода поиска условного экстремума: Метод замены переменной Метод множителей Лагранжа

Метод замены переменной Рассмотрим нахождение экстремума функции нескольких переменных не на всей области определения, а на множестве, удовлетворяющему некоторому условию. Пусть задана функция z=f(x,y), аргументы которой удовлетворяют уравнению g(x,y)=C, называемому уравнением связи.

Метод замены переменной Чтобы найти условный экстремум, нужно из уравнения связи выразить одну переменную через другую: y=φ(x). Подставим это выражение в функцию двух переменных и получим функцию одной переменной: z=f(x,y)=f(x, φ(x)). Ее экстремум и будет условным экстремумом функции z=f(x,y).

Метод замены переменной (пример) Найти точки максимума и минимума функции

Метод замены переменной (решение)

УСЛОВНЫЙ ЭКСТРЕМУМ В этом примере связь между х и у оказалась линейной, поэтому уравнение связи легко разрешилось относительно одной из переменных. Но в некоторых случаях это сделать довольно сложно. Поэтому в общем случае для нахождения условного экстремума используется метод множителей Лагранжа.

метод множителей Лагранжа Рассмотрим функцию трех переменных: Функция Лагранжа

метод множителей Лагранжа (теорема)

метод множителей Лагранжа Следовательно, для нахождения условного экстремума функции z=f(x,y) при условии g(x,y)=C, требуется найти решение системы: Последнее уравнение совпадает с уравнением связи.

метод множителей Лагранжа Первые два уравнения можно записать в виде: То есть в точках условного экстремума градиенты функций f(x,y) и g(x,y) коллинеарны.

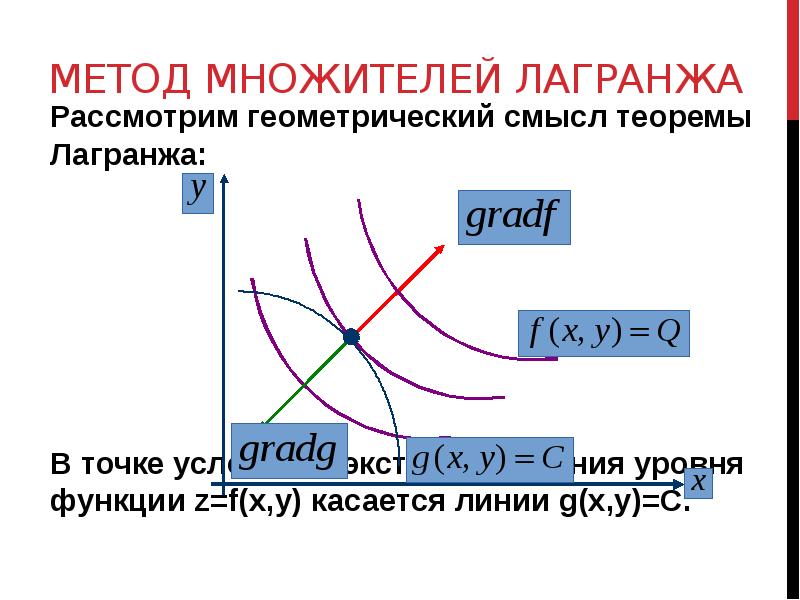
метод множителей Лагранжа Рассмотрим геометрический смысл теоремы Лагранжа: В точке условного экстремума линия уровня функции z=f(x,y) касается линии g(x,y)=C.

Спасибо за внимание