Накопленная частота и др презентация
Содержание
- 2. Предположим, есть список чисел, представляющий собой количество книг, которые каждый студент
- 3. 3, 3, 5, 6, 6, 6, 8 вверху левой колонки пишем
- 4. Накопленная частота отвечает на вопрос "сколько раз встречается в списке данное
- 6. Чтобы определить накопленную частоту для второго значения списка, необходимо прибавить его
- 8. Проверьте полученные результаты: В итоге мы сложили абсолютные частоты всех значений
- 10. Дискретные данные Дискретные данные можно посчитать, они не дробятся на более
- 11. Непрерывные данные Непрерывные данные часто не поддаются конечному счету, между двумя
- 12. Частости – это… Существуют относительные показатели, характеризующие долю частоты отдельных вариантов
- 13. Мода и медиана Мода – это величина признака (варианта), которая чаще всего
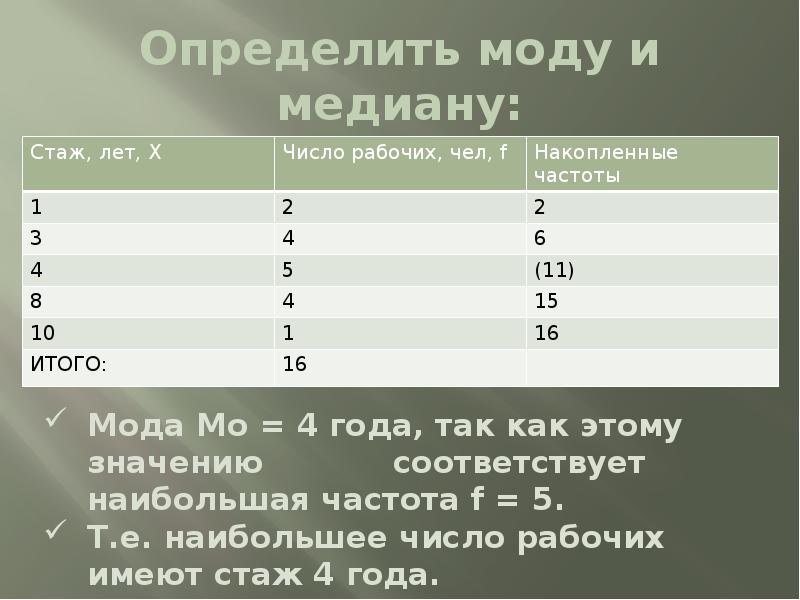
- 14. Определить моду и медиану:
- 15. Медиана Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот.
- 16. Медиана Ме = 4 года. Т.е. половина рабочих имеет стаж меньше четырех
- 17. Свойство медианы Главное свойство Ме в том, что сумма абсолютных отклонений значений признака
- 18. Медиана. Пример 2: Найти медиану дискретного ряда 16,13,15,10,19,22,25,12,18,14,19,14,16,10. Решение. Ранжируем ряд: 10,10,12,13,14,14,15,16,16,18,19,19,22,25,
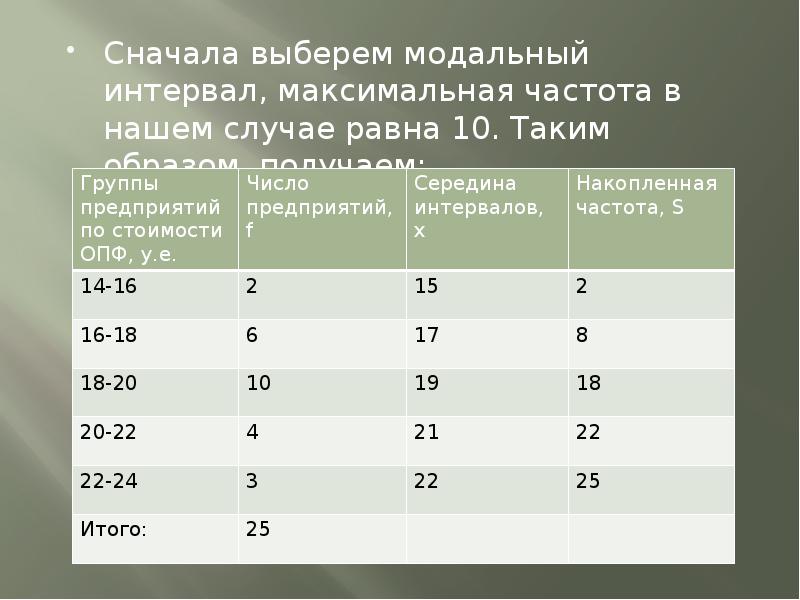
- 21. Сначала выберем модальный интервал, максимальная частота в нашем случае равна 10.
- 22. Мода. Расчеты 1) По максимальной частоте найдем модальный интервал: Fmax=10 → I = 18-20
- 23. Медиана. Расчеты: Нам даны интервалы. 1) Найдем медианный интервал по накопленной
- 24. Медиана. Расчеты: 2) По соответствующей формуле Медиана Ме =18+2[(25+1)/2 - 8/10]=18,9 млн.руб.
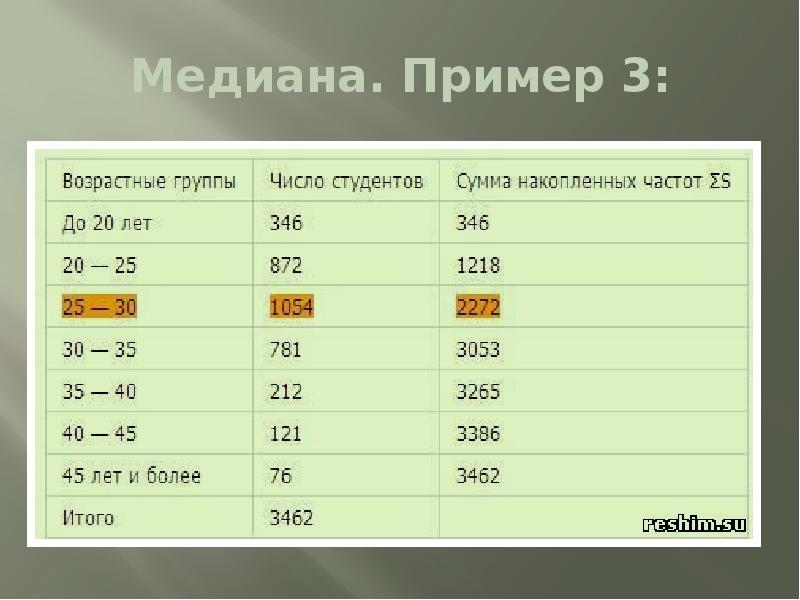
- 25. Медиана. Пример 3:
- 26. Решение: Медианный интервал находится в возрастной группе 25-30 лет, так
- 27. Решение: Далее подставляем в формулу необходимые числовые данные и получаем значение
- 28. Спасибо за внимание!
- 29. Скачать презентацию





















![Медиана. Расчеты:
2) По соответствующей формуле
Медиана Ме =18+2[(25+1)/2 - 8/10]=18,9 млн.руб.
Медиана. Расчеты:
2) По соответствующей формуле
Медиана Ме =18+2[(25+1)/2 - 8/10]=18,9 млн.руб.](/documents_7/ab7f12bcab6db2fd60687dbfed8b42d0/img23.jpg)



Слайды и текст этой презентации
Похожие презентации





























