Первообразная и интеграл 11 класс презентация

Определение Функция F(х) называется первообразной функции f(х) на промежутке Х, если На практике промежуток Х обычно не указывают, но подразумевают (область определения функции). Например: функция у = х² является первообразной для функции у=2х, т.к. для любого х справедливо (х²)´ = 2х.

Теорема 1 Если функция f(х) непрерывна при , то для f(х) существует первообразная F(х) на Х.

Теорема 2 Если F(x) одна из первообразных функции f(x), на промежутке Х, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид у = F(x)+C.

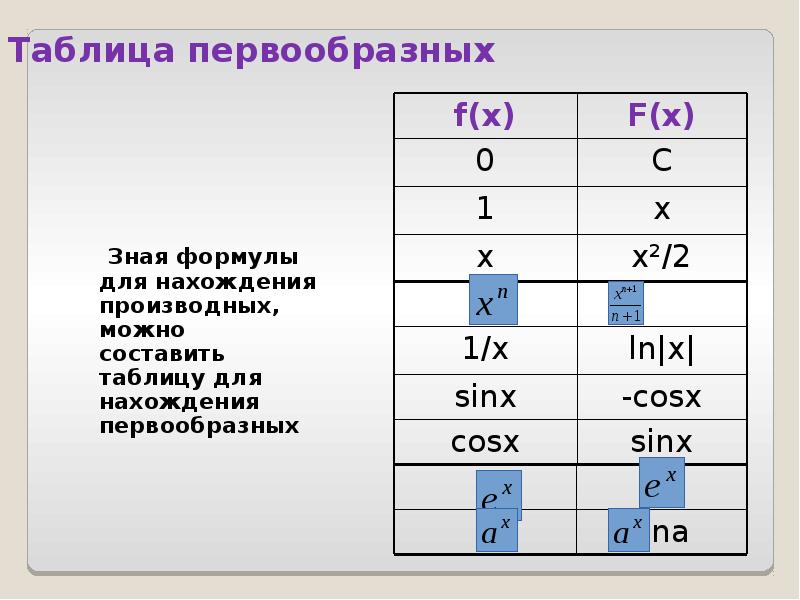
Таблица первообразных Зная формулы для нахождения производных, можно составить таблицу для нахождения первообразных

Правила нахождения первообразных Первообразная суммы равна сумме первообразных Если F(x) – первообразная для f(x), то к·F(x) – есть первообразная для к· f(x). Если F(x) – первообразная для f(x), то первообразной для функции у= f(кx+m) служит функция у = 1/к· F(кx+ m)

1.Проверь себя. Соотнеси выражения в правом и левом столбцах Если f(x) равно: 1) f(x)=2х+х³ 2) f(x)=4х-2 3) f(x)=х³-3х²+х-1 4) f(x)=4х⁵+2х+е 5) f(x)=х⁴+3х²+5 6) f(x)=5cosx-3sin2x

2. Ответить на вопрос: какая функция является перообразной для функции f(x)= 2sinx – cosx? А) cosx - 2sinx Б) 2cosx - sinx В) -2cosx - sinx Г) –cosx + 2sinx

3. Выберите ответ, при котором предложение будет верно. Функция F(x) является первообразной для функции f(x), если: А) F'(x) = f(x) Б) F'(x) = - f(x) В) f'(x) = F(x) Г) f(x) = F(x)

4. Ответить на вопрос: для какой функции первообразной является функция F(x)=2x³+6x²+x-9? А) f(x) = 1/4·x⁴+2x³+x²-9x Б) f(x) = 2x⁴+6x³+x²-9x В) f(x) = 6x²+12x+1 Г) f(x) = x⁴⁄2+2x³+1/2·x²-9x

5. Ответить на вопрос: производная какой из функций равна у = 4х - 3х²? А) F(x) = 2x³-2x²+C Б) F(x) = 2x²-1/3·x+C В) F(x) = 2x²-x³+C Г) F(x) = 4x²-x⁴+C

Записать в тетрадь. Записать в тетрадь. Примеры с решениями

Задание №1. Найдите первообразную функции f(x), график которой проходит через точку А. а) f(x)=5х+х², А(0;3) б) f(x)=3х - 5, А(4;10) Решение. а) Найдём первообразные F(x)= 5х²⁄2+х³⁄3+ С, где С – произв.число. Найдём это С: т.к. график проходит через точку А(0;3), то F(0)= 5·0²⁄2+0³⁄3+ С = С и равно 3. С=3 Значит производная, график которой проходит через т. А, имеет вид: F(x)= 5х²⁄2+х³⁄3+3.

б) f(x)=3х - 5, А(4;10) Решение. F(x)= 3х²⁄2-5х+С, где С – произв. число. F(4)= 3·4²⁄2-5·4+С=24-20+С=4+С и 4+С=10 => С=6, тогда F(x)= 3х²⁄2-5х+6 Ответ: F(x)= 3х²⁄2-5х+6

Выполни самостоятельно Найдите первообразную функции f(x), график которой проходит через точку А, если: 1) f(x)=х²-5, А(3;4) 2) f(x)=2х²+3, А(-2;-5) 3) f(x)=(х-2)², А(0;2) 4) f(x)=cos3x, А(0;1)

Задание №2. Найдите первообразную функции f(x), значение которой при х = х₀ равно у₀. а) f(x)=10х⁴+х; х₀=0; у₀=6 Решение. F(x)= 10х⁵⁄5 + х²⁄2 + С = = 2х⁵+ х²⁄2 +С, где С – произв. число. Найдём С. Т.к. по условию F(x₀)=у₀, то F(0)=2·0⁵+0²⁄2+С=С и равно у₀= 6. Значит ответ: F(x)=2х⁵+х²⁄2+6

б) f(x)=2sin3x+4cos(x/2); х₀=π⁄3; у₀=0 Решение. F(x)=-2·1/3·cos3x+4·2 sin(x/2)+С= =-2/3·cos3x+8· sin(x/2)+С, где С- пр. ч. Найдём С. Т.к. по условию F(x₀)=у₀, то F(π⁄3)=-2/3·cos π+8sin(π/6)+С= =2/3+8·1/2+С=4(2/3)+С и равно 0. Тогда С = -4(2/3). Значит F(x)=-2/3·cos3x+8· sin(x/2)-4(2/3)

в) f(x)=4+6х²; х₀=2; у₀<0 Решение. F(x)= 4х+6х³⁄3+С, где С-п.ч. Найдём С: т.к. F(х₀)= у₀ , то F(2)= 4·2+6·2³⁄3+С= 8+16+С=24+С и 24+С <0 => С <-24. Пусть это будет (-25). Тогда ответ F(x)= 4х+6х³⁄3-25

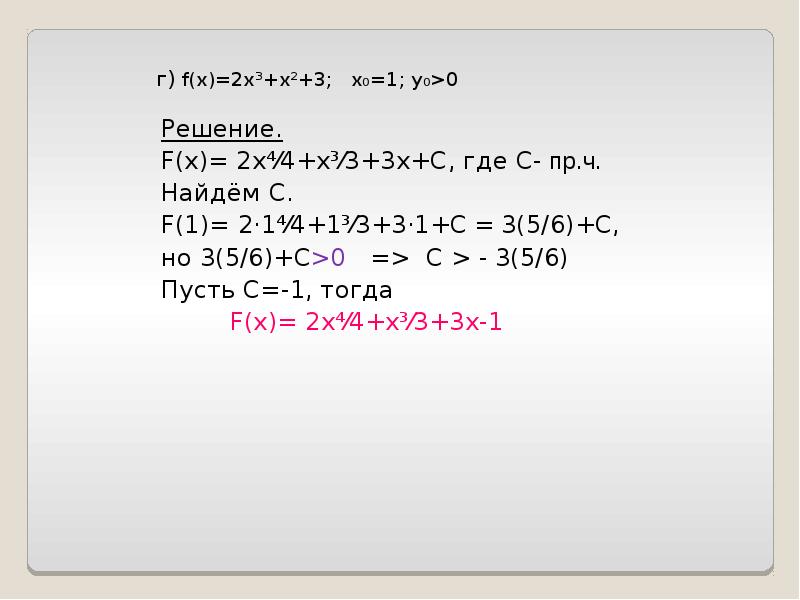
г) f(x)=2х³+х²+3; х₀=1; у₀>0 Решение. F(x)= 2х⁴⁄4+х³⁄3+3х+С, где С- пр.ч. Найдём С. F(1)= 2·1⁴⁄4+1³⁄3+3·1+С = 3(5/6)+С, но 3(5/6)+С>0 => С > - 3(5/6) Пусть С=-1, тогда F(x)= 2х⁴⁄4+х³⁄3+3х-1

ИНТЕГРАЛЫ ИНТЕГРАЛЫ

ИНТЕГРАЛ

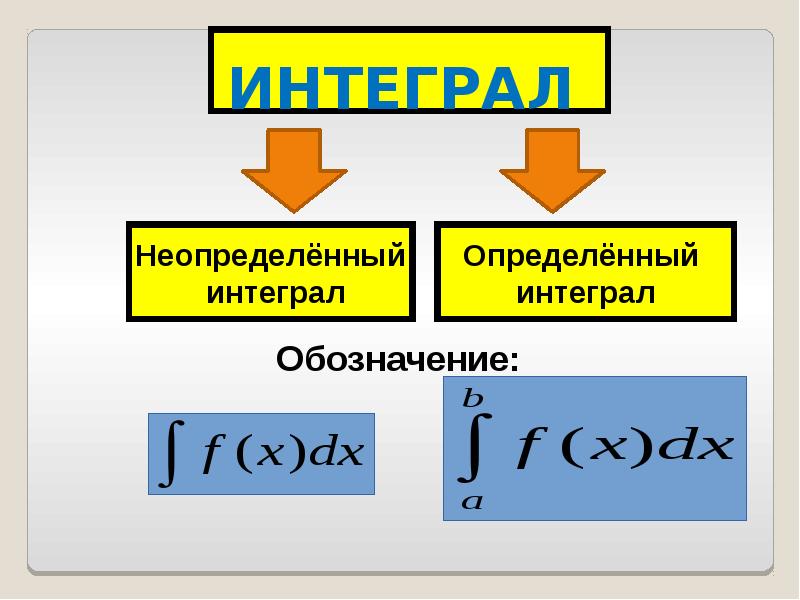
НЕОПРЕДЕЛЁННЫЙ НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Определение: Множество всех первообразных функции f(x) на некотором промежутке называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается

Таблица интегралов

Определение Процесс нахождения интеграла называется интегрированием. Интегрирование является операцией, обратной  дифференцированию

Историческая справка Интегрирование прослеживается еще в древнем Египте, примерно в 1800 г. до н.э, Московский математический папирус демонстрирует знание формулы объёма усеченной пирамиды.

Историческая справка метод исчерпывания Евдокса (примерно 370 до н.э.), который пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже были известны.

Историческая справка Этот метод был подхвачен и развит Архимедом, и использовался для расчета площадей, парабол и приближенного расчета площади круга.

Историческая справка Аналогичные методы были разработаны не зависимо в Китае в 3-м веке н.э. Лю Хуэйем, который использовал их для нахождения площади круга.

Историческая справка Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для нахождения объема шара

Историческая справка Следующий крупный шаг в исследование интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсаном ( известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла, чтобы найти объем параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвертой степени.

Новая тема. Всё записать в тетрадь

ОПРЕДЕЛЁННЫЙ ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и пусть F(x) – некоторая ее первообразная. Тогда число F(b)–F(a) называется интегралом от а до b функции f(x) и обозначается

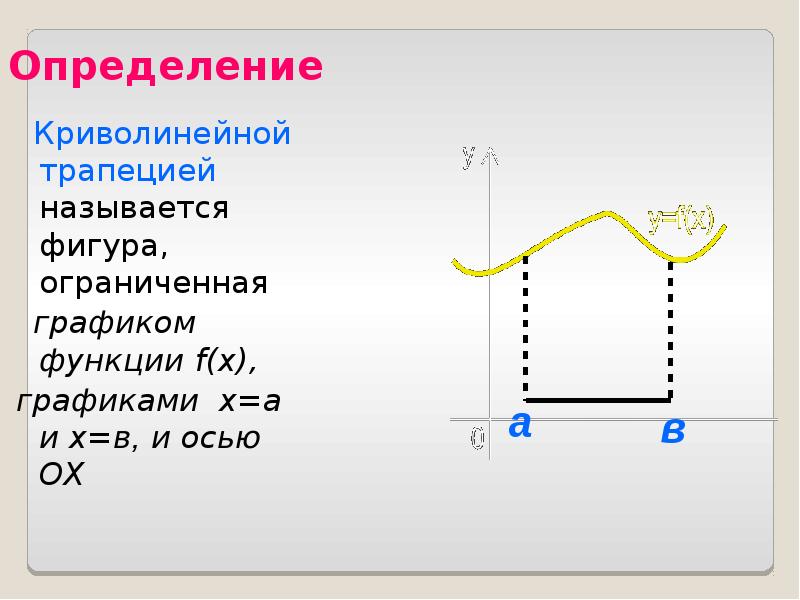
Определение Криволинейной трапецией называется фигура, ограниченная графиком функции f(x), графиками х=а и х=в, и осью ОХ

Формула Ньютона-Лейбница Теорема: если функция у = f(x) непрерывна на отрезке [а;в], то справедлива формула Опираясь на эту формулу получаются следующие свойства определенного интеграла

Свойства определенного интеграла

Свойства определенного интеграла

Алгоритм вычисления площади криволинейной трапеции Схематично изобразить график функции f(x). Провести прямые x=a и x=b. Записать одну из первообразных F(x) функции f(x). Составить и вычислить разность F(b) – F(a).

Вычислить площадь фигуры, ограниченной линиями, используя формулу Ньютона-Лейбница Вариант 1 f(x) = 2x – 3 y = 0, x = 3, x = 5

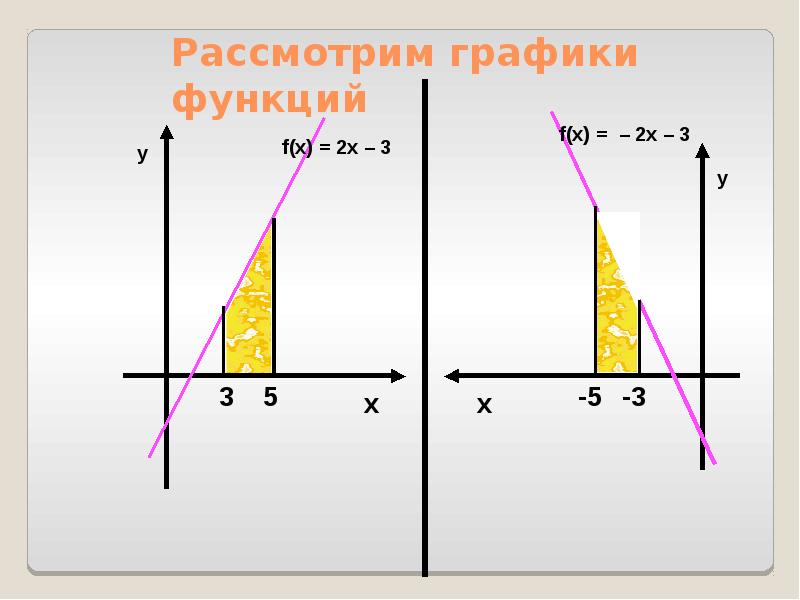
Рассмотрим графики функций

Запомним Геометрический смысл определенного интеграла – это площадь криволинейной трапеции Физический смысл определенного интеграла – это… (Найди и запиши сам!)

Найти площадь фигуры, ограниченной линиями 1) y=–3x²–2, x=1, x=2, y=–1 2) у= 4x–x², y=0 3) y= x²–2x+3, x+y=5 4) y=x², y=x

Используемые ресурсы