Плоскость и прямая в пространстве презентация

Плоскость и прямая в пространстве

Определение. Уравнением поверхности в пространстве называется такое уравнение между переменными которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.

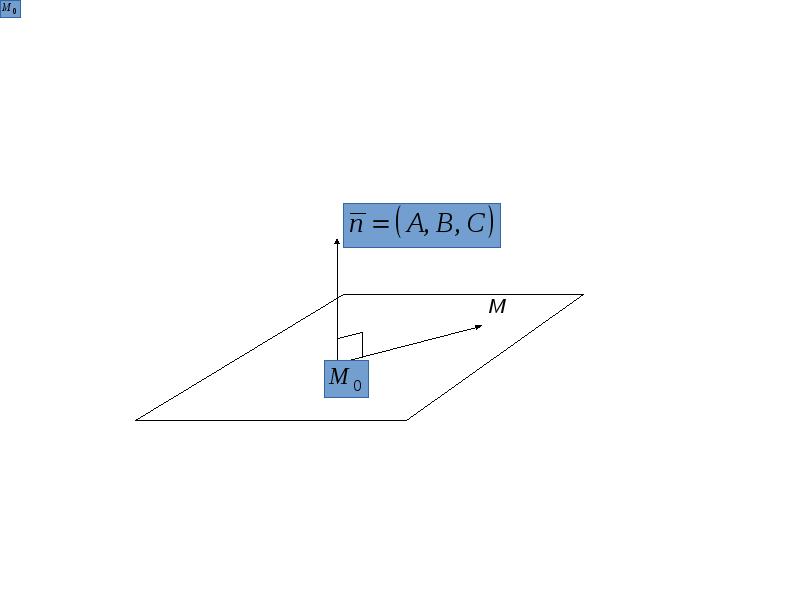
Назовем нормалью к плоскости вектор, перпендикулярный к этой плоскости. Обозначают нормаль

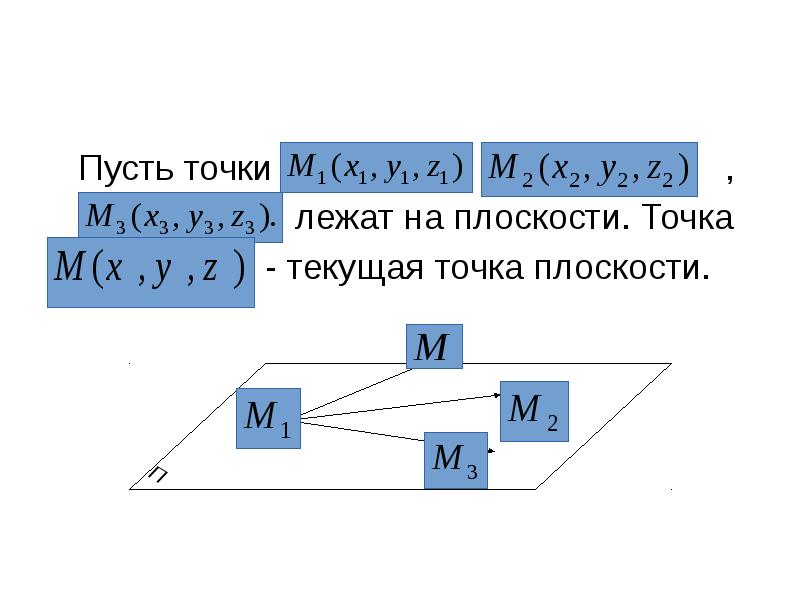
Уравнение плоскости, проходящей через заданную точку Пусть точки и лежат на плоскости . Тогда и, значит, их скалярное произведение равно нулю: это уравнение плоскости, проходящей через точку перпендикулярно вектору .

общее уравнение плоскости Из предыдущего уравнения легко получить общее уравнение плоскости

Частные случаи общего уравнения 1. плоскость проходит через начало координат. 2. плоскость параллельна оси OX. 3. плоскость параллельна плоскости XOY. 4. Плоскость проходит через ось OX. 5. плоскость является плоскостью XOY. Остальные случаи рассмотреть самостоятельно.

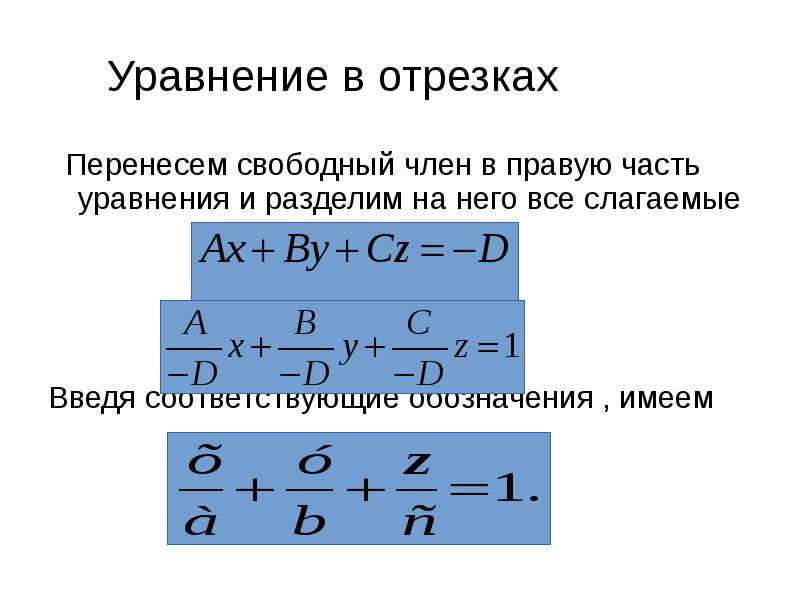
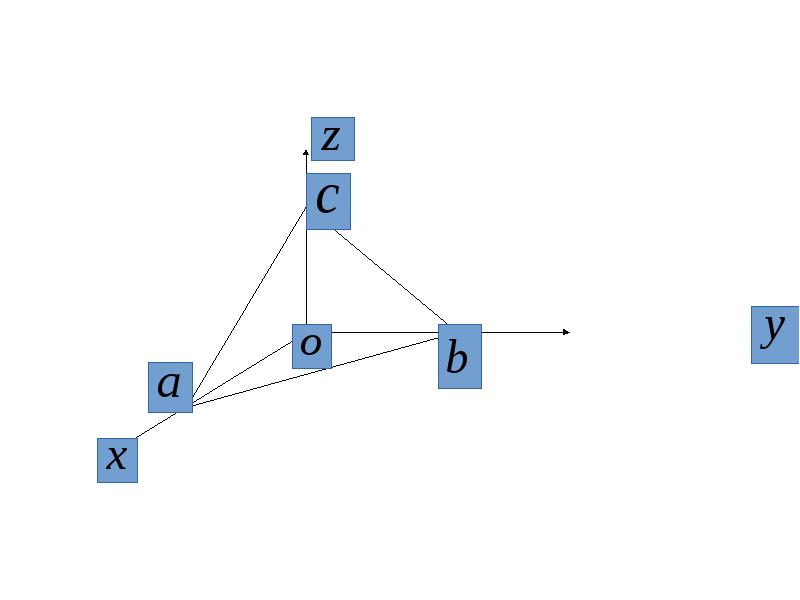
Уравнение в отрезках Перенесем свободный член в правую часть уравнения и разделим на него все слагаемые Введя соответствующие обозначения , имеем .

Уравнение плоскости, проходящей через три точки Пусть точки , , лежат на плоскости. Точка - текущая точка плоскости.

Запишем координаты векторов: Эти векторы компланарны, т.к. лежат в одной плоскости. Следовательно их смешанное произведение равно нулю. Получаем уравнение:

Уравнение плоскости, проходящей через три точки

Взаимное расположение плоскостей

Угол между плоскостями Даны две плоскости и : Тогда:

Условие перпендикулярности плоскостей Если плоскости перпендикулярны друг к другу, то соответственно перпендикулярны их нормальные векторы

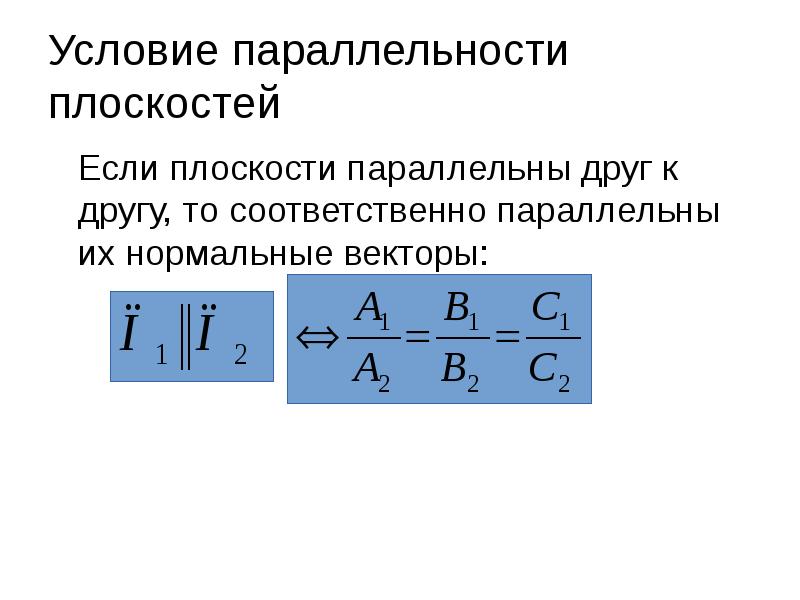
Условие параллельности плоскостей Если плоскости параллельны друг к другу, то соответственно параллельны их нормальные векторы:

Расстояние от точки до плоскости

Пример Найти уравнение плоскости, проходящей через точки

Решение В уравнение плоскости, проходящей через три точки, подставим координаты данных точек: Раскладывая определитель по элементам первой строки, имеем .

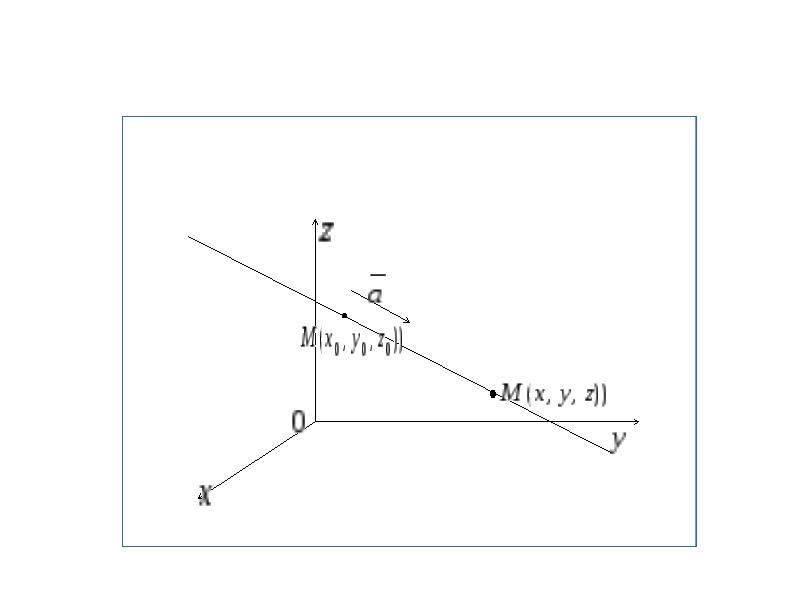
Прямая в пространстве.

Канонические уравнения прямой. -направляющий вектор прямой, -точка прямой. Тогда

Параметрические уравнения (вывести самостоятельно) t-переменный параметр.

Уравнение прямой, проходящей через две точки Точки и лежат на прямой. Вывод уравнения сделать самостоятельно.

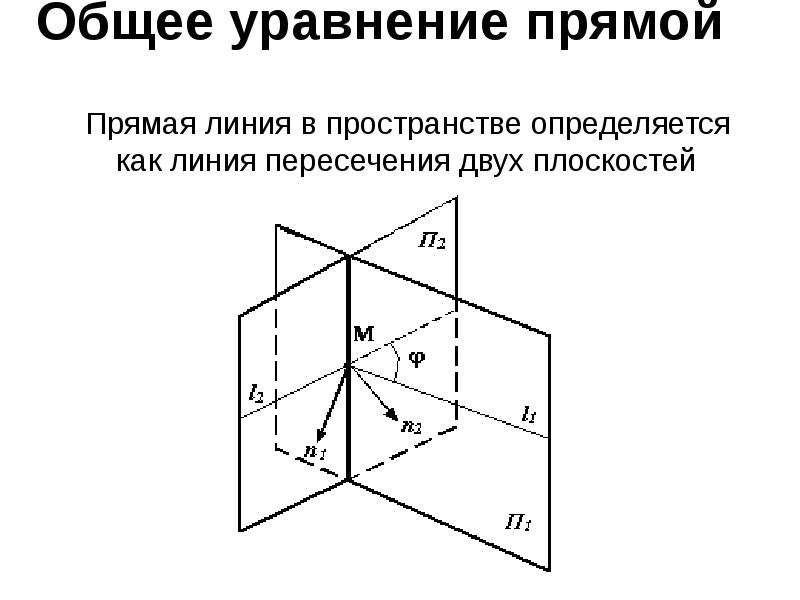
Общее уравнение прямой Прямая линия в пространстве определяется как линия пересечения двух плоскостей

каждое уравнение отдельно- это уравнение плоскости, которые пересекаются по прямой.

Пример Записать канонические уравнения прямой, заданной общими уравнениями Решение. Найдем точку на прямой. Пусть, например, z = 0. Система примет вид

Сложив уравнения, получим Тогда из второго уравнения Точка на прямой А(1; -2; 0).

Найдем направляющий вектор этой прямой: Получим канонические уравнения прямой

Взаимное расположение прямых в пространстве

Угол между прямыми Угол между прямыми равен углу между их направляющими векторами

Параллельность прямых Если то

Перпендикулярность прямых Если то

Взаимное расположение прямой и плоскости

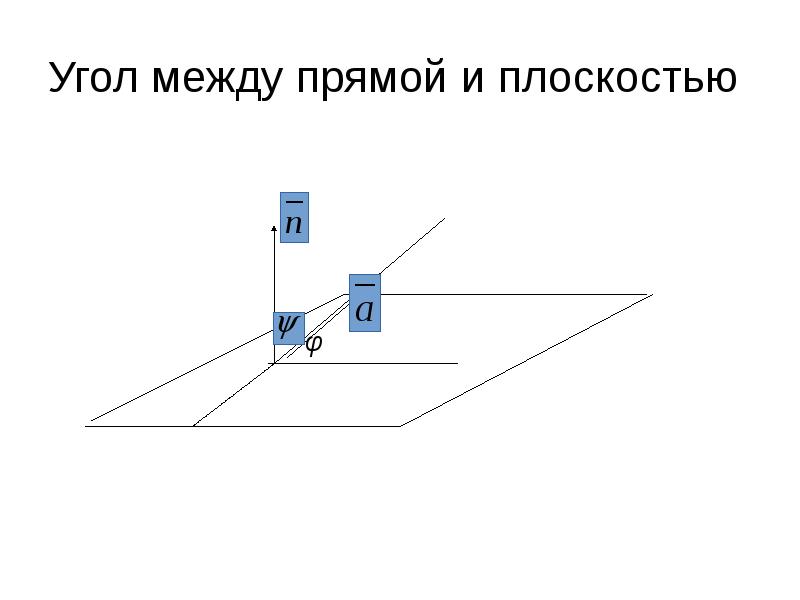
Угол между прямой и плоскостью

Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на плоскость

Угол между прямой и плоскостью -нормаль плоскости П, -направляющий вектор прямой .

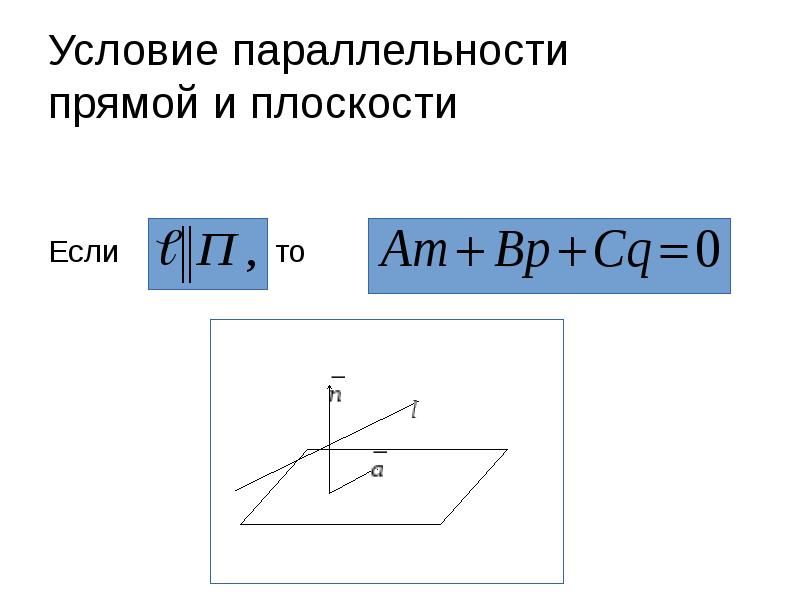
Условие параллельности прямой и плоскости Если то

Условие перпендикулярности прямой и плоскости Если то

Точка пересечения прямой и плоскости Пусть требуется найти точку пересечения прямой и плоскости Запишем параметрические уравнения прямой и подставим выражения для х, у, z в уравнение плоскости.

Получим уравнение вида относительно параметра t. Выразив t из этого уравнения и подставив в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости.

Замечание. Если уравнение относительно t примет вид 0t = 0 (то есть M = N = 0), то любое действительное значение t будет его решением, значит, прямая и плоскость имеют множество общих точек, то есть прямая лежит в плоскости.

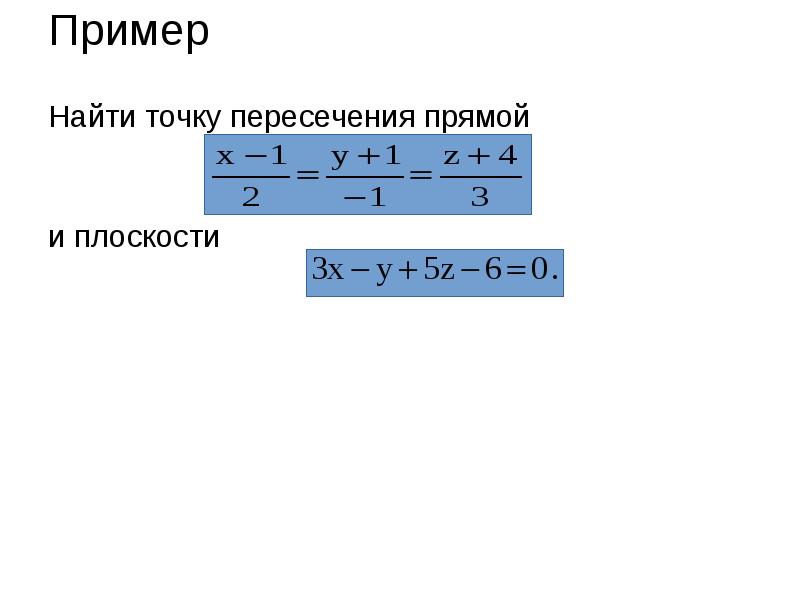
Пример Найти точку пересечения прямой и плоскости

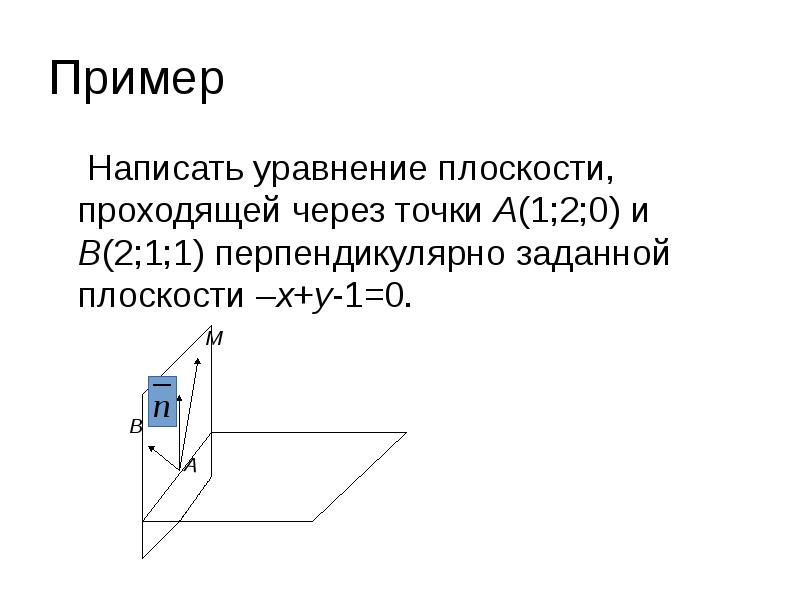
Пример Написать уравнение плоскости, проходящей через точки А(1;2;0) и В(2;1;1) перпендикулярно заданной плоскости –х+у-1=0.

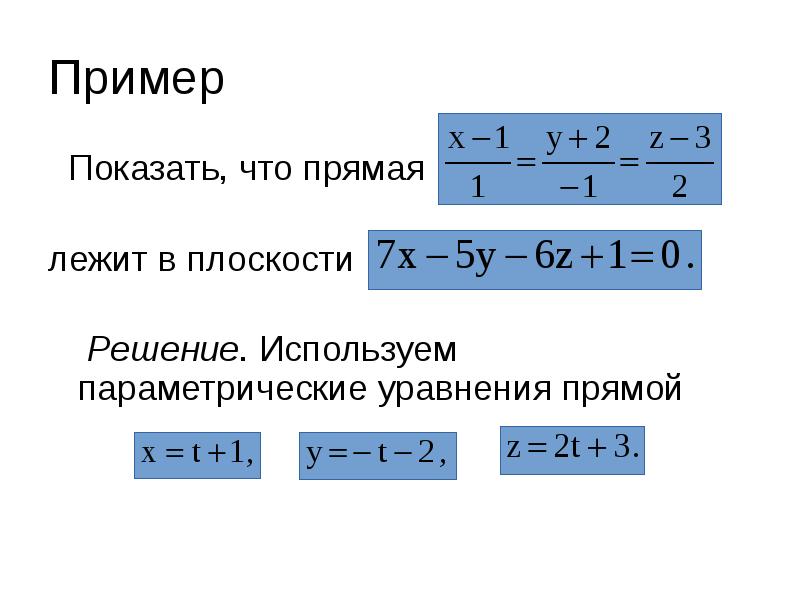
Пример Показать, что прямая лежит в плоскости Решение. Используем параметрические уравнения прямой

Подставим в уравнение плоскости: - Получили равенство, верное при любых Следовательно, прямая лежит в плоскости.

Пример Найти уравнение перпендикуляра к плоскости , проходящего через точку А(2;-1:3), и определить координаты основания этого перпендикуляра.