Правильные многогранники вокруг нас презентация

Правильные многогранники вокруг нас.

Содержание. 1.Определение правильных многогранников. 2.Существование пяти типов правильных многогранников. 3.Правильный тетраэдр. 4.Куб (гексаэдр). 5.Октаэдр. 6.Додекаэдр. 7.Икосаэдр. 8.Историческая справка. 9.Правильные многогранники в природе и на практике. 10.Список литературы.

Многогранник называется правильным, если:

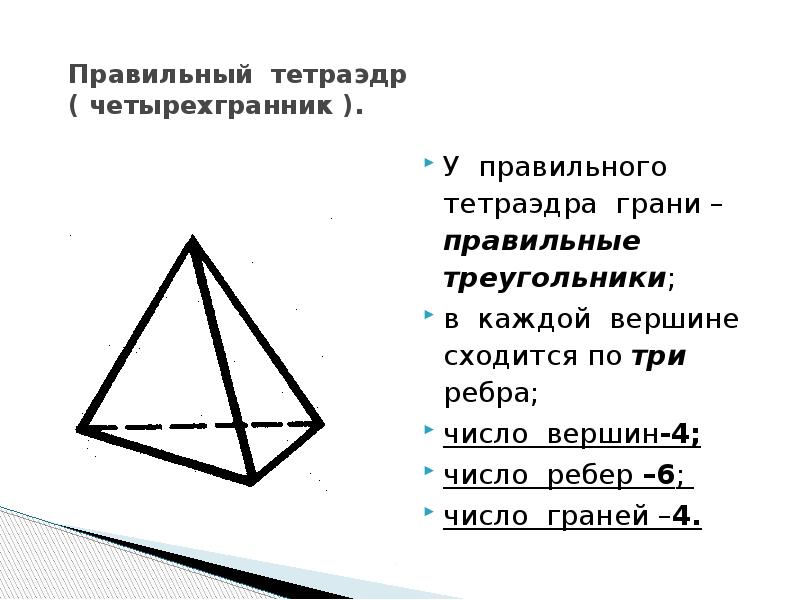
Правильный тетраэдр ( четырехгранник ). У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра; число вершин-4; число ребер –6; число граней –4.

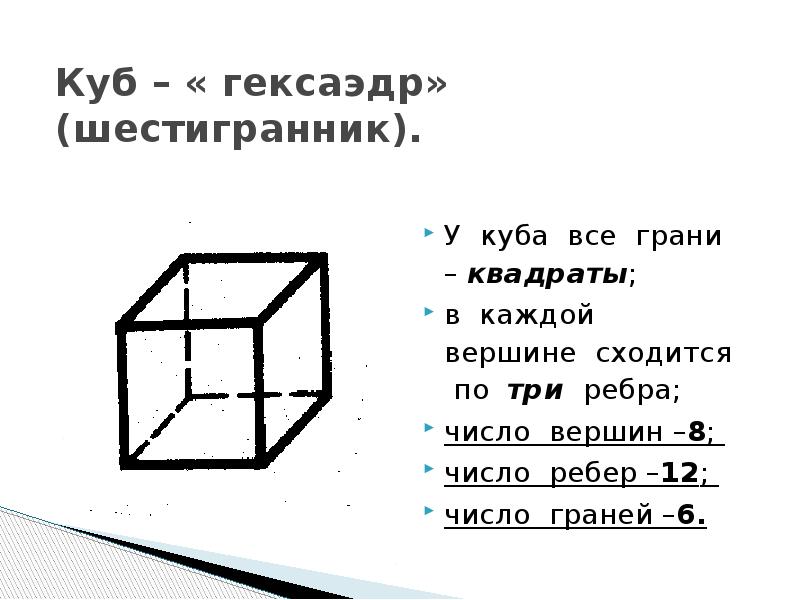
Куб – « гексаэдр» (шестигранник). У куба все грани – квадраты; в каждой вершине сходится по три ребра; число вершин –8; число ребер –12; число граней –6.

Октаэдр (восьмигранник ). У октаэдра грани –правильные треугольники; в каждой вершине сходится по четыре ребра; число вершин -6; число ребер -12; число граней –8.

Додекаэдр (двенадцатигранник). У додекаэдра грани - правильные пятиугольники; в каждой вершине сходится по три ребра; число вершин –20; число ребер –30; число граней –12.

Икосаэдр (двадцатигранник ). У икосаэдра грани –правильные треугольники; в каждой вершине сходится по пять ребер; число вершин –12; число ребер –30; число граней –20.

Историческая справка. Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, XIII книга знаменитых «Начал» Евклида. Эти многогранники часто называют также платоновыми телами – в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном, четыре из них олицетворяли четыре стихии: тетраэдр –огонь, куб –землю, икосаэдр –воду, октаэдр –воздух; пятый же многогранник, додекаэдр, символизировал все мироздание - его по-латыни стали называть quinta essentia ( «пятая сущность»).

Правильные многогранники в природе и на практике. Формы правильных многогранников имеют природные кристаллы, например: куб –монокристалл поваренной соли NaCl, октаэдр –монокристалл алюмокалиевых квасцов; форму додекаэдра – кристаллы пирита –сернистого колчедана FeS. Многие архитектурные сооружения или их детали представляют собой правильные многогранники.

Модели правильных многогранников.

Список литературы. Энциклопедический словарь юного математика. –М., «Педагогика»,1989.-352с.:ил. Земляков А.Н. Геометрия в 9 классе. –М., «Просвещение»,1988.-176с.:ил. Энциклопедия элементарной математики, том 4 –Геометрия. –М.,1966.-568с.:ил. http://repetitor-problem.net/pravilnyie-mnogogranniki https://videouroki.net/razrabotki/pravilnye-mnogogranniki-vokrug-nas.html

Спасибо за внимание и Спасибо за внимание и сотрудничество. Желаю удачи! 