Раздел: Прямоугольная система координат на плоскости презентация
Содержание
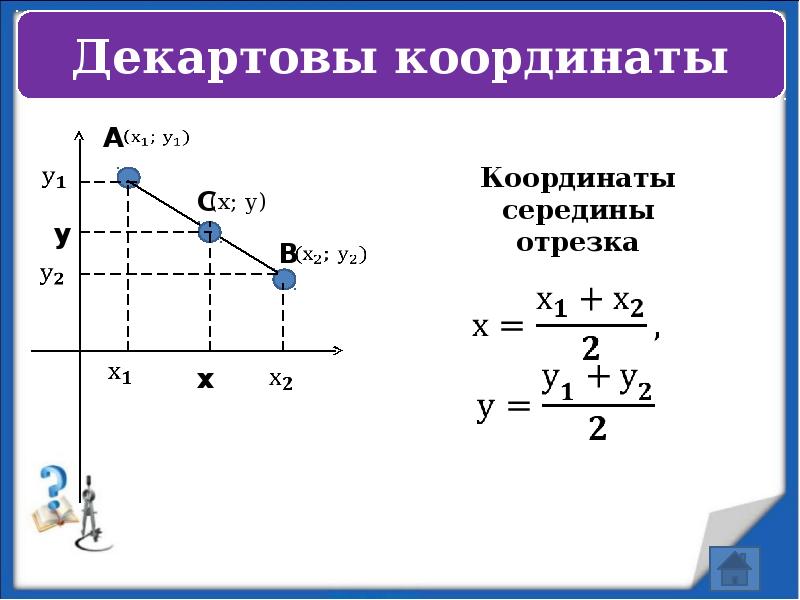
- 2. Цели обучения: 8.1.3.15 находить координаты середины отрезка; 8.1.3.16 находить координаты точки,
- 4. Пример 1
- 5. А(2; 6) А(2; 6) В(4; 7) С(8; 10)
- 6. Задача о делении отрезка в данном отношении состоит в том, чтобы
- 7. Пример: Даны точки М1(1; 1) и М2(7; 4). Найти точку М,
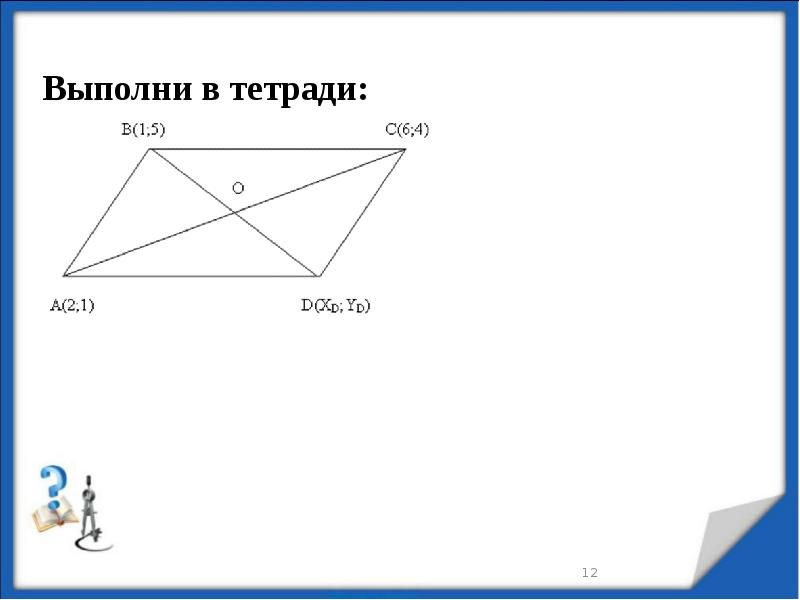
- 10. Задание № 1 Найдите координаты середины отрезка АВ, если :
- 11. Задание № 2 Найдите координаты точки, делящей отрезок АВ в отношении
- 13. Скачать презентацию










Слайды и текст этой презентации
Скачать презентацию на тему Раздел: Прямоугольная система координат на плоскости можно ниже:
Похожие презентации





























