Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped harmonic oscillations. (Lecture 1) презентация

Physics 2 Voronkov Vladimir Vasilyevich

Lecture 1 Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped harmonic oscillations. Driven harmonic oscillations.

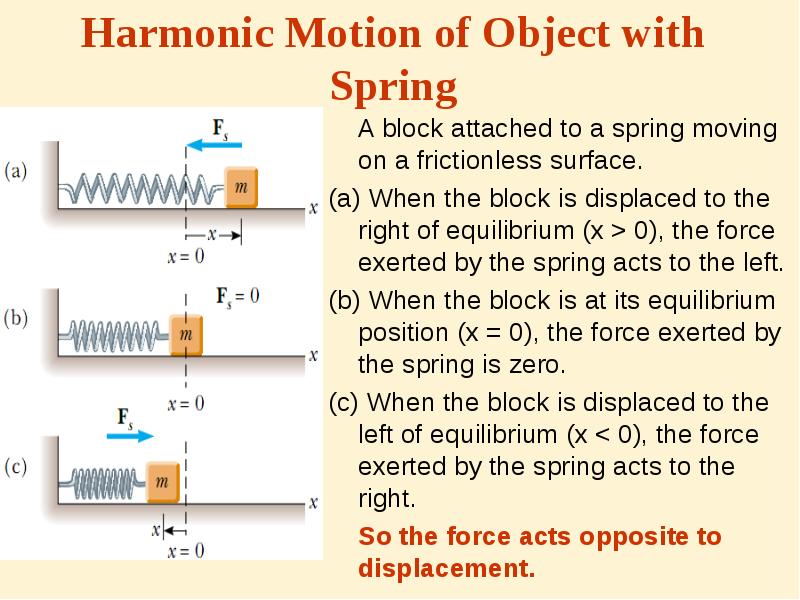
Harmonic Motion of Object with Spring A block attached to a spring moving on a frictionless surface. (a) When the block is displaced to the right of equilibrium (x > 0), the force exerted by the spring acts to the left. (b) When the block is at its equilibrium position (x = 0), the force exerted by the spring is zero. (c) When the block is displaced to the left of equilibrium (x < 0), the force exerted by the spring acts to the right. So the force acts opposite to displacement.

x is displacement from equilibrium position. x is displacement from equilibrium position. Restoring force is given by Hook’s law: Then we can obtain the acceleration: That is, the acceleration is proportional to the position of the block, and its direction is opposite the direction of the displacement from equilibrium.

Simple Harmonic Motion An object moves with simple harmonic motion whenever its acceleration is proportional to its position and is oppositely directed to the displacement from equilibrium.

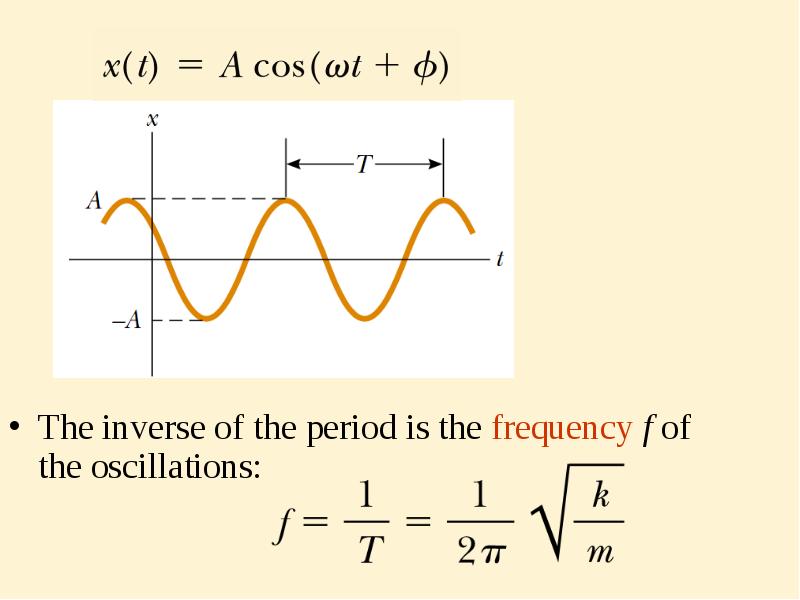
Mathematical Representation of Simple Harmonic Motion So the equation for harmonic motion is: We can denote angular frequency as: Then: Solution for this equation is:

A=const is the amplitude of the motion =const is the angular frequency of the motion =const is the phase constant t+is the phase of the motion T=const is the period of oscillations:

The inverse of the period is the frequency f of the oscillations:

Then the velocity and the acceleration of a body in simple harmonic motion are: Then the velocity and the acceleration of a body in simple harmonic motion are:

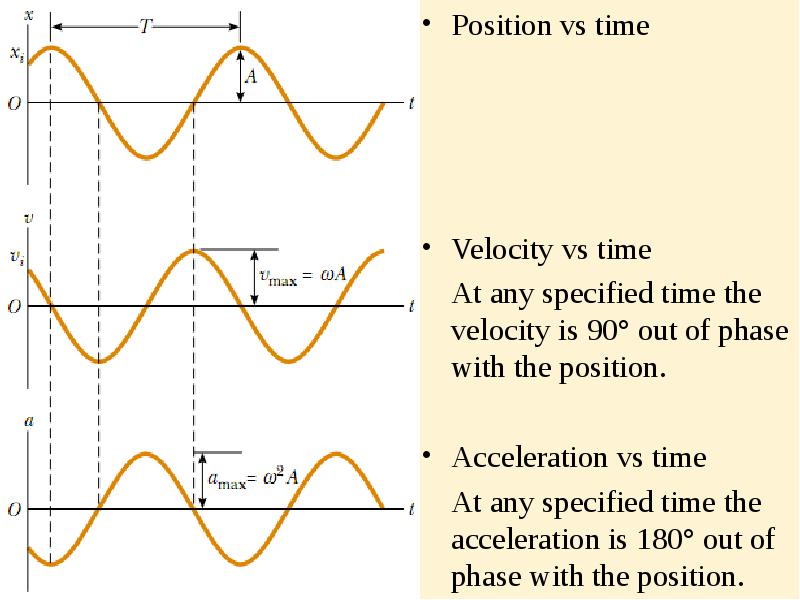
Position vs time Position vs time Velocity vs time At any specified time the velocity is 90° out of phase with the position. Acceleration vs time At any specified time the acceleration is 180° out of phase with the position.

Energy of the Simple Harmonic Oscillator Assuming that: no friction the spring is massless Then the kinetic energy of system spring-body corresponds only to that of the body: The potential energy in the spring is:

The total mechanical energy of simple harmonic oscillator is: The total mechanical energy of simple harmonic oscillator is: That is, the total mechanical energy of a simple harmonic oscillator is a constant of the motion and is proportional to the square of the amplitude.

Simple Pendulum Simple pendulum consists of a particle-like bob of mass m suspended by a light string of length L that is fixed at the upper end. The motion occurs in the vertical plane and is driven by the gravitational force. When  is small, a simple pendulum oscillates in simple harmonic motion about the equilibrium position  0. The restoring force is -mgsin, the component of the gravitational force tangent to the arc.

The Newton’s second law in tangential direction: The Newton’s second law in tangential direction: For small values of  Solution for this equation is:

The period and frequency of a simple pendulum depend only on the length of the string and the acceleration due to gravity. The period and frequency of a simple pendulum depend only on the length of the string and the acceleration due to gravity. The simple pendulum can be used as a timekeeper because its period depends only on its length and the local value of g.

Physical Pendulum If a hanging object oscillates about a fixed axis that does not pass through its center of mass and the object cannot be approximated as a point mass, we cannot treat the system as a simple pendulum. In this case the system is called a physical pendulum.

Applying the rotational form of the second Newton’s law: Applying the rotational form of the second Newton’s law: The solution is: The period is

Damped Harmonic Oscillations In many real systems, nonconservative forces, such as friction, retard the motion. Consequently, the mechanical energy of the system diminishes in time, and the motion is damped. The retarding force can be expressed as R=-bv (b=const is the damping coefficient) and the restoring force of the system is -kx then:

The solution for small b is The solution for small b is When the retarding force is small, the oscillatory character of the motion is preserved but the amplitude decreases in time, with the result that the motion ultimately ceases.

The angular frequency can be expressed through k/m)1/2 – the natural frequency of the system (the undamped oscillator): The angular frequency can be expressed through k/m)1/2 – the natural frequency of the system (the undamped oscillator):

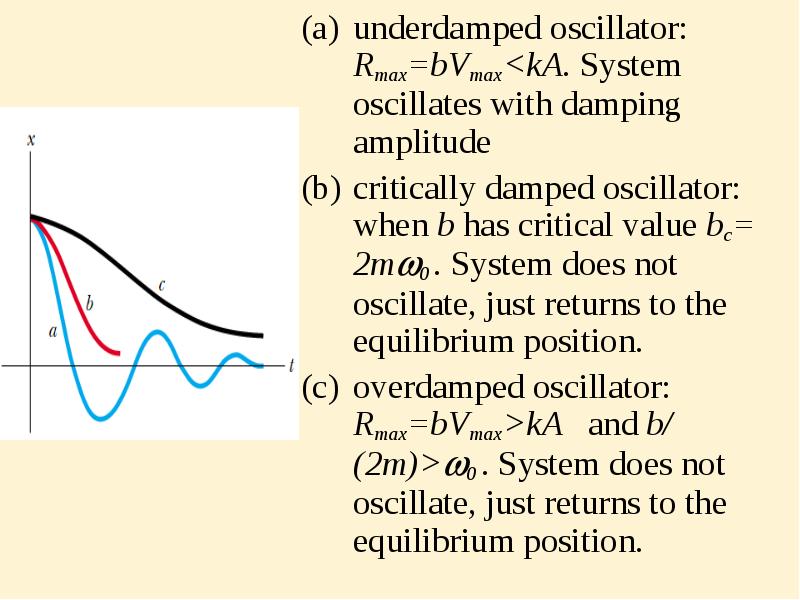
underdamped oscillator: Rmax=bVmax<kA. System oscillates with damping amplitude underdamped oscillator: Rmax=bVmax<kA. System oscillates with damping amplitude critically damped oscillator: when b has critical value bc= 2m0 . System does not oscillate, just returns to the equilibrium position. overdamped oscillator: Rmax=bVmax>kA and b/(2m)>0 . System does not oscillate, just returns to the equilibrium position.

Driven Harmonic Oscillations A driven (or forced) oscillator is a damped oscillator under the influence of an external periodical force F(t)=F0sin(t). The second Newton’s law for forced oscillator is: The solution of this equation is:

The forced oscillator vibrates at the frequency of the driving force The forced oscillator vibrates at the frequency of the driving force The amplitude of the oscillator is constant for a given driving force. For small damping, the amplitude is large when the frequency of the driving force is near the natural frequency of oscillation, or when ≈. The dramatic increase in amplitude near the natural frequency is called resonance, and the natural frequency  is also called the resonance frequency of the system.

Resonance So resonance happens when the driving force frequency is close to the natural frequency of the system: ≈At resonance the amplitude of the driven oscillations is the largest. In fact, if there were no damping (b = 0), the amplitude would become infinite when  This is not a realistic physical situation, because it corresponds to the spring being stretched to infinite length. A real spring will snap rather than accept an infinite stretch; in other words, some for of damping will ultimately occur, But it does illustrate that, at resonance, the response of a harmonic system to a driving force can be catastrophically large.

Units in Si spring constant k N/m=kg/s2 damping coefficient b kg/s phase  rad (or degrees) angular frequency  rad/s frequency f 1/s period T s