Диполь. Поле диполя презентация

Электричество и магнетизм. Лектор: Парахин А.С., к. ф.-м. наук, доцент.

1.4. Диполь. Поле диполя. Часто электрическое поле создаёт не один заряд, а целая система зарядов. Тогда расчёт электрического поля изменяется. Одной из самых распространённых систем зарядов является система из двух зарядов, равных по величине и противоположных по направлению.

Определение диполя. Определение. Система зарядов, состоящая из двух точечных равных и противоположных по знаку зарядов, называется электрическим диполем. Вектор, идущий от отрицательного заряда к положительному, называется плечом диполя.

По принципу суперпозиции: Найдём электрическое поле, создаваемое диполем. Обозначим расстояние между зарядами , а величину положительного заряда . Тогда потенциал поля будет равен сумме потенциалов, создаваемых зарядами по отдельности.

Потенциал поля диполя. Необходимо только иметь в виду, что один потенциал будет положителен, второй – отрицателен: . Здесь – расстояние от положительного заряда до точки наблюдения, – расстояние от отрицательного заряда до точки наблюдения, – электростатическая константа.

Преобразование формулы. Приведём в скобках к общему знаменателю:

Преобразование знаменателя. Если точка наблюдения отстоит достаточно далеко от диполя, то в знаменателе, можно считать, стоит квадрат расстояния от центра диполя до точки наблюдения .

Преобразование числителя. В числителе же стоит произведение расстояния между зарядами диполя на косинус угла между плечом диполя и направлением на точку наблюдения как показано на рисунке.

Дипольный момент. Так что Определение. Физическая величина, численно равная произведению положительного заряда диполя на плечо диполя, называется электрическим моментом диполя или дипольным моментом.

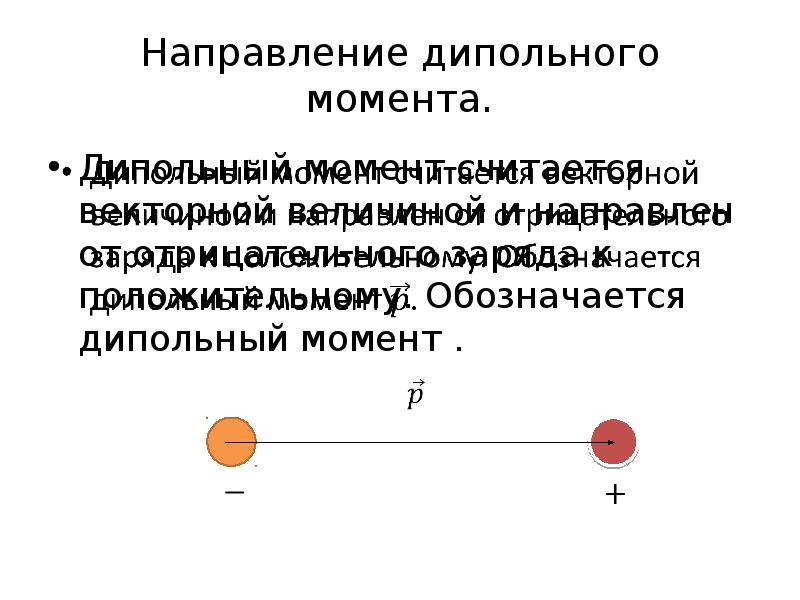
Направление дипольного момента. Дипольный момент считается векторной величиной и направлен от отрицательного заряда к положительному. Обозначается дипольный момент .

Следствия из определения. 1. Вектор. Направлен от отрицательного заряда к положительному. 2. Размерность.

Потенциал поля диполя. С помощью понятия дипольного момента потенциал поля диполя можно записать следующим образом:

Потенциал поля диполя. Умножим эту формулу на и разделим на : В числителе стоит скалярное произведение дипольного момента и радиуса-вектора точки наблюдения. Так что

Напряжённость поля диполя. Чтобы найти напряжённость поля диполя, нужно найти градиент потенциала:

Координата x напряжённости поля диполя. Найдём этот градиент по координатам:

Проекции напряжённости на другие оси. Аналогично:

Вектор напряжённости поля диполя. Все эти три равенства можно записать одним векторным: Это и есть окончательная формула напряжённости электрического поля диполя.

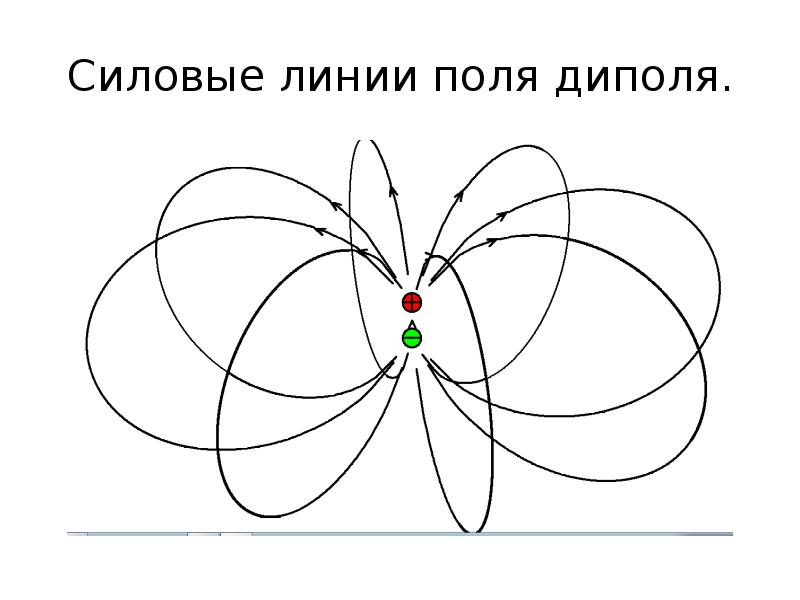
Силовые линии поля диполя.

Программа Progr D: Progr E: Progr F: Progr G: Progr H:

1.5.Пондеромоторные силы. Определение. Пондеромоторными силами называются силы, действующие на тела со стороны различного рода полей. Рассмотрим силы действующие на электрические заряды в электрическом поле.

Сила, действующая на одиночный заряд Согласно определению напряжённости электрического поля, она представляет собой силу, действующую на единицу заряда, помещённого в данную точку пространства: Отсюда можно найти силу, которая действует на заряд со стороны электрического поля:

Сила, действующая на систему зарядов. Если в поле внесена система зарядов, то согласно принципу суперпозиции сила будет равна сумме сил, действующих на каждый заряд:

Сила, действующая на диполь. Предположим теперь, что в электрическое поле внесён диполь, а поле при этом является однородным, т.е. напряжённость его во всех точках пространства одинаковая.

Равенство нулю сил. Тогда на заряды диполя будут действовать равные по величине, но противоположные по направлению силы и . Равенство этих сил и их антипараллельность означает, что результирующая сила, действующая на диполь равна нулю. Таким образом в однородном электрическом поле равнодействующая всех сил, действующих на диполь, равна нулю.

Момент сил, действующих на диполь. Найдём момент сил. Первый сомножитель в последнем векторном произведении равен дипольному моменту, так что момент сил, действующих на диполь, определяется его дипольным моментом:

Модуль момента сил. Найдём модуль этого момента: Из этой формулы видно, что максимальный по модулю момент соответствует углу и между дипольным моментом и напряжённостью электрического поля.

Равновесие диполя Нулевой момент соответствует углам и . При этих углах дипольный момент остаётся в покое, если до этого покоился, т.е. находится в состоянии равновесия. Но для угла это равновесие устойчиво, а для угла – неустойчиво. Малейшее отклонение от этого положения приводит к вращению диполя. Он стремится к положению, когда угол между его моментом и напряжённостью поля равен нулю.

Демонстрация поворота диполя в электрическом поле.

Энергия диполя в электрическом поле. Найдём энергию диполя в электрическом поле. Обозначим потенциал поля в точке, где находится отрицательный заряд, а потенциал в точке, где находится положительный заряд. Ось абсцисс направлена вдоль электрического поля.

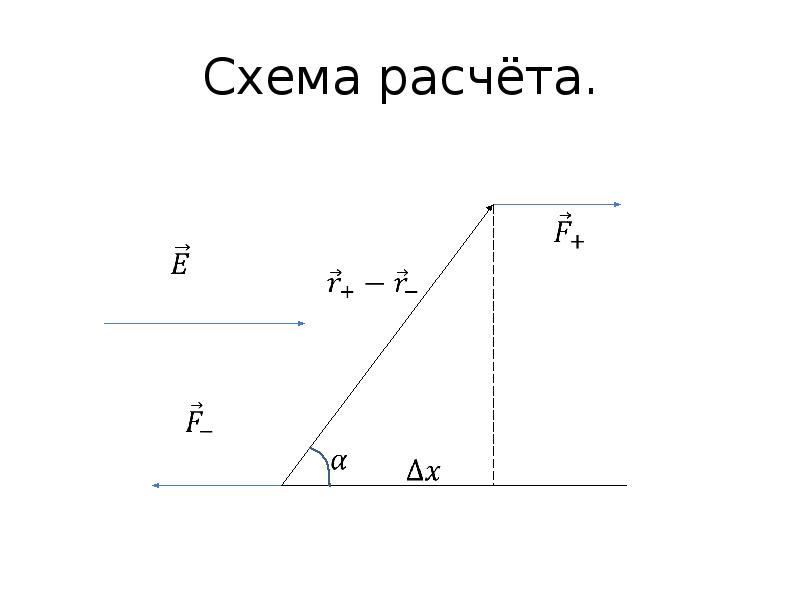
Схема расчёта.

Потенциальная энергия диполя. Тогда энергия диполя может быть найдена по формуле: =

Работа по перемещению пробного заряда. Здесь – угол между напряжённостью поля и дипольным моментом. А Так что:

Минимум и максимум потенциальной энергии диполя. Таким образом, потенциальная энергия диполя равна скалярному произведению напряжённости на дипольный момент. При этом минимум потенциальной энергии соответствует нулевому углу между напряжённостью электрического поля и дипольным моментом, а максимум углу . Стремление к минимуму пот. энергии.

Сила, действующая на диполь в неоднородном поле. Наконец, найдём силы, действующие на диполь в неоднородном электрическом поле. Для этого воспользуемся связью между силой и потенциальной энергией:

Преобразование формул Как было показано ранее: Тогда

Формула силы Дипольный момент от координат не зависит, значит дифференцировать нужно только напряжённость электрического поля:

Координаты силы Из этой формулы можно найти проекции силы на оси координат:

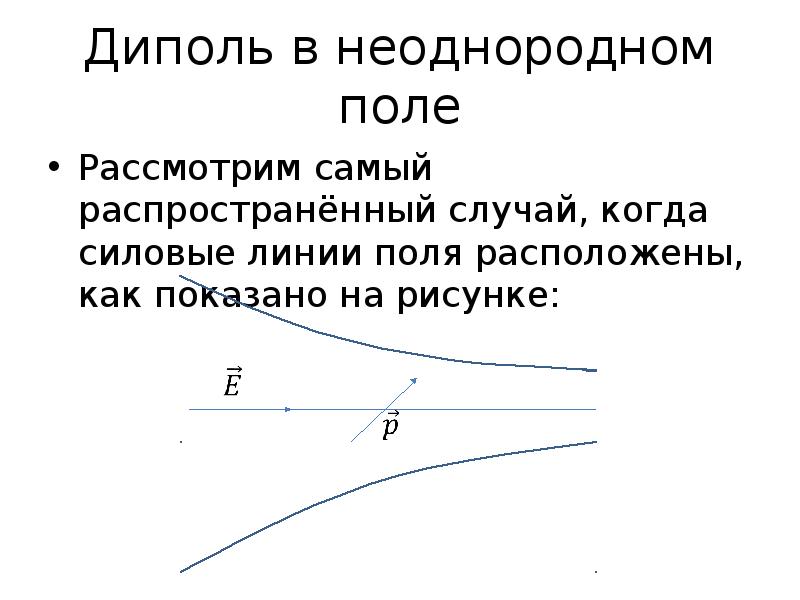
Диполь в неоднородном поле Рассмотрим самый распространённый случай, когда силовые линии поля расположены, как показано на рисунке:

Проекция силы на ось ox В этом случае координаты вектора напряжённости электрического поля вдоль осей ординат и аппликат равны нулю, поэтому энергия диполя вычисляется по формуле: а силу можно рассчитать по формуле:

1.6.Прямой расчёт поля системы зарядов. Часто система зарядов представляет собой не точечные заряды, как у диполя, а непрерывное распределённые заряды. При этом в одной точке пространства зарядов может быть больше, в другой – меньше.

Объёмная плотность заряда. Для характеристики распределения зарядов по пространству вводят понятие объёмной плотности заряда. Определение. Объёмной плотностью заряда называется физическая величина, численно равная заряду единицы объёма.

Следствия из определения. Обозначается и по определению равна: Из определения следует: 1.Плотность заряда – скаляр; 2.Разменрность плотности заряда:

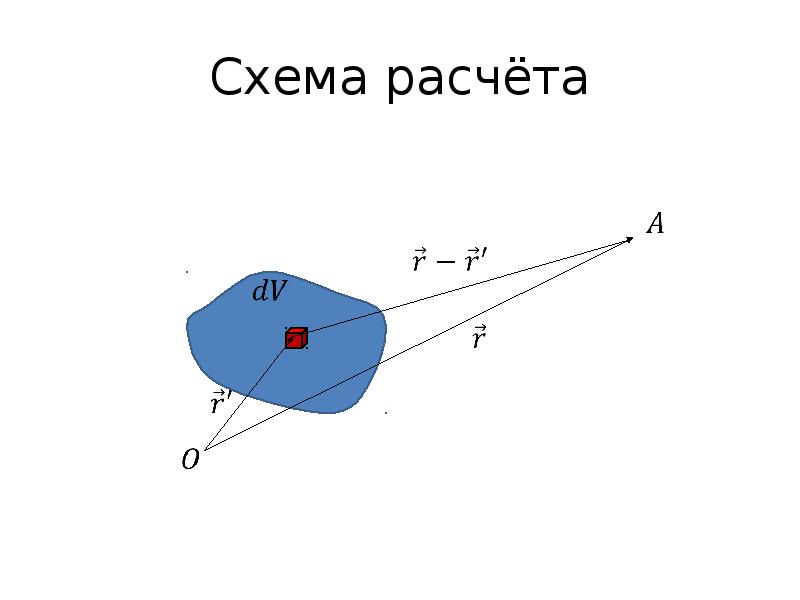
Схема расчёта

Элемент заряда Выделим внутри системы зарядов элементарный объём , размеры которого малы во всех направлениях. Этому объёму будет соответствовать элементарный заряд

Элемент потенциала Благодаря малости размеров этого заряда, его можно считать точечным, и для определения потенциала поля, которое он создаёт, можно воспользоваться формулой потенциала точечного заряда. При этом нужно иметь в виду, что потенциал, который создаёт элементарный заряд, также будет элементарным:

Полный потенциал всей системы зарядов. Чтобы найти потенциал поля, создаваемого всей системой зарядов, нужно проинтегрировать по всему объёму: Эта формула и представляет собой формулу прямого расчёта поля системы зарядов.

Поверхностная система зарядов. Расчёт поля с помощью прямого метода бывает сложным. Иногда расчёт упрощается, если система зарядов имеет специальную форму. Например – поверхностная система зарядов.

Поверхностная система зарядов Определение. Система зарядов, расположенная на некоторой поверхности, называется поверхностной системой зарядов.

Поверхностная плотность зарядов. Определение. Поверхностной плотностью заряда называется физическая величина, численно равная заряду единицы площади поверхности. Обозначается поверхностная плотность , и по определению она равна:

Следствия из определения. Из определения следует: 1.Поверхнстная плотность – скаляр; 2.Размерность:

Потенциал поверхностной системы зарядов. С помощью понятия поверхностной плотности напряжённость поля, создаваемого поверхностной системой зарядов, может быть рассчитана по формуле:

Линейная система зарядов Определение. Система зарядов, расположенных на некоторой кривой линии, называется линейной системой зарядов.

Линейная плотность зарядов. Определение. Линейной плотностью заряда называется физическая величина, численно равная заряду единицы длины кривой, на которой расположен заряд.

Следствия из определения. Обозначается линейная плотность и по определению равна: Из определения следует: 1.Линейная плотность – скаляр; 2.Размерность:

Потенциал линейной системы зарядов. С помощью линейной плотности потенциал линейной системы зарядов можно найти по формуле:

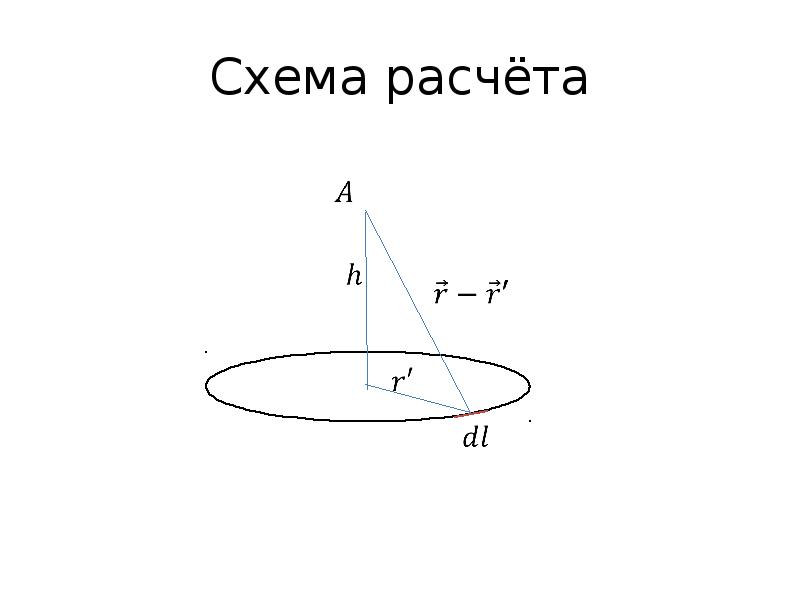
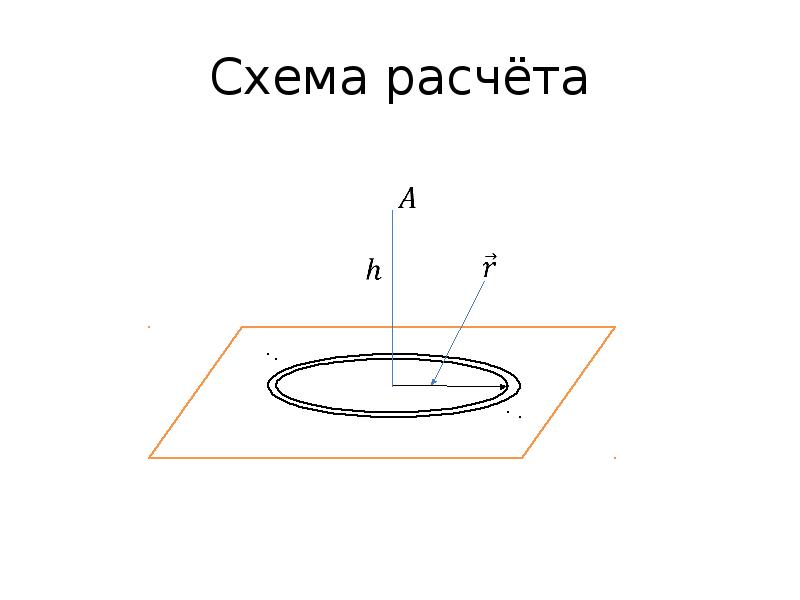
Потенциал поля заряженного кольца. Пусть заряд расположен на окружности. Требуется найти потенциал, создаваемый таким зарядом на прямой, проходящей через центр окружности, перпендикулярно её плоскости. Выделим на окружности элемент длины и обозначим расстояние от точки наблюдения до центра окружности через , как показано на рисунке:

Схема расчёта

Преобразование формул Расстояние от элемента окружности до точки наблюдения равно: и остаётся неизменным в процессе интегрирования. Так что интеграл будет равен:

Поле в центре кольца. В частности в центре окружности:

Напряжённость поля кольца Найдём проекцию напряжённости электрического поля на направление перпендикуляра к плоскости окружности, проходящего через центр.

Поле на больших расстояниях от кольца. Из этой формулы в частности следует: если , то формула превращается в формулу напряжённости точечного заряда: Это частный случай более общего утверждения, что на больших расстояниях поле любой системы зарядов можно считать полем точечного заряда.

Потенциал заряженного отрезка прямой Найдём теперь потенциал однородно заряженного отрезка прямой, как показано на рисунке:

Потенциал отрезка Для этого снова воспользуемся общей формулой потенциала для линейной системы зарядов с учётом того, что отрезок расположен вдоль оси . При этом начало оси совпадает с основанием перпендикуляра из точки наблюдения на ось.

Преобразования. Здесь

Расчёт интеграла Подставим это всё в формулу потенциала: Этот интеграл табличный, он равен:

Замена тригонометрических функций. Заменим тригонометрические функции отношением соответствующих отрезков: Здесь – координата левого конца отрезка, – то же самое только для правого конца отрезка.

Преобразования формул. Тогда формулу потенциала можно преобразовать следующим образом:

Потенциал заряженного отрезка. Упростим выражение, приведя к общему знаменателю во всех членах дробей: Так выражается потенциал отрезка прямой.

Потенциал над серединой отрезка В частности, если точка наблюдения находится над серединой отрезка:

Потенциал над серединой отрезка Тогда формула потенциала упрощается:

Предельные случаи. Отсюда, в частности, следует, что при потенциал стремится к нулю, при потенциал стремится к плюс бесконечности.

Потенциал для бесконечного отрезка Найдём потенциал бесконечного отрезка. Для этого будем считать, что длина отрезка на много больше расстояния до точки наблюдения. Тогда в числителе параметром можно пренебречь.

Преобразование знаменателя. В знаменателе этим параметром пренебречь нельзя, т.к. в этом случае знаменатель обращается в нуль. В знаменателе мы воспользуемся приближением , бинома Ньютона:

Преобразование формул Для этого вынесем из-под знака корня:

Разность потенциалов в двух точках пространства около заряженной прямой. Из этой формулы в частности следует, что разность потенциалов в двух точках, находящихся на расстоянии и от прямой находится по формуле:

Напряжённость поля заряженной прямой. Снова найдём проекцию напряжённости электрического поля на направление перпендикуляра к прямой. Напряжённость вблизи бесконечного заряженного отрезка обратно пропорциональна расстоянию от прямой до точки наблюдения.

Заряженная плоскость. Найдя потенциал поля заряженной окружности, можно найти поле заряженной плоскости. Для этого в плоскости выделим кольцо радиуса и шириной с центром, расположенным под точкой наблюдения, как показано на рисунке.

Схема расчёта

Потенциал поля окружности Согласно формуле определения потенциала окружности: – это полный заряд всей окружности. В нашем случае кольцо можно считать окружностью, т.к. его толщина элементарна.

Элемент поля, создаваемого кольцом Кроме того, заряд, который ему соответствует и потенциал, который он создаёт, также элементарны. Так что: Чтоб найти полный потенциал, нужно проинтегрировать. Но сначала будем считать, что плоскость не бесконечно большая, а представляет собой круг достаточно большого радиуса .

Преобразование формул Тогда интегрирование нужно вести в пределах от нуля и до радиуса большого круга.

Предельные случаи Это и есть формула потенциала заряженного круга над его центром. Из неё, в частности, следует: если , то потенциал стремится к нулю, если , то потенциал стремится к конечной величине: . Если при этом и радиус круга стремится к бесконечности, то и потенциал стремится к бесконечности.

Потенциал для бесконеченой плоскости Если радиус круга на много больше, чем , круг можно считать бесконечной плоскостью, а величиной под корнем можно пренебречь, и формула потенциала упростится:

Разность потенциалов. Из этой формулы, в частности следует, что разность потенциалов в двух точках, находящихся на расстояниях и , равна:

Напряжённость бесконечной плоскости. Найдём напряжённость электрического поля круга над его центом на небольшом расстоянии.