Экспериментальные факты, лежащие в основе теории магнетизма презентация
Содержание
- 2. Для двух бесконечно длинных проводников Ампер установил: Сила Ампера для взаимодействия
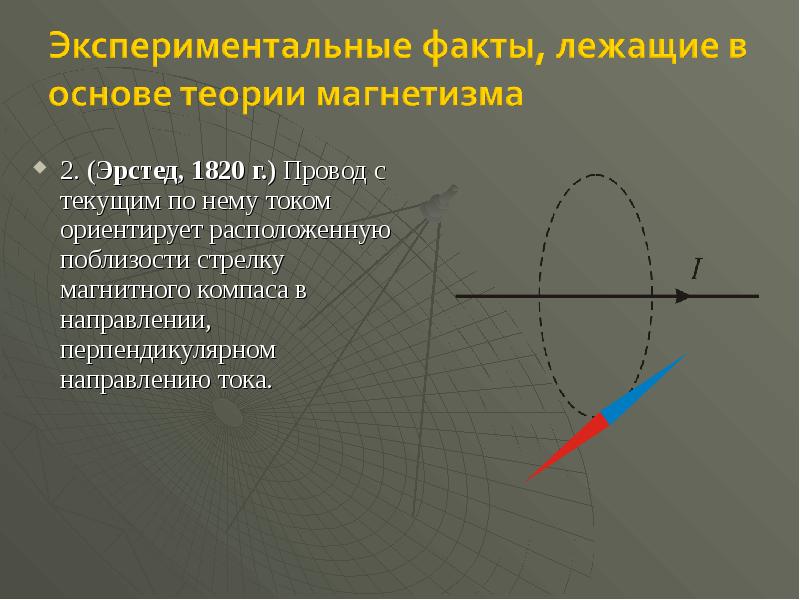
- 3. 2. (Эрстед, 1820 г.) Провод с текущим по нему током ориентирует
- 4. 2. (Эрстед, 1820 г.) Если вместо магнитной стрелки рядом с прямолинейным
- 5. Магнитное поле (МП) – силовое поле в пространстве, окружающем токи и
- 6. ИСТОЧНИКИ МП Движущийся электрический заряд. Электрический ток Постоянный магнит
- 7. Основная силовая характеристика МП – вектор магнитной индукции Основная силовая
- 8. За направление МП в данной точке принимают направление, вдоль которого располагается
- 9. ПРАВИЛО БУРАВЧИКА За направление положительной нормали принимается направление поступательного движения буравчика,
- 10. СИЛОВЫЕ ЛИНИИ МП Силовые линии МП(линии магнитной индукции) – линии касательные,
- 11. Линии вектора B прямолинейного проводника с током – концентрические окружности с
- 12. Линии вектора B кругового витка с током пересекают плоскость витка перпендикулярно
- 13. МОДУЛЬ ВЕКТОРА Магнитная индукция зависит от силы тока I
- 14. МОДУЛЬ ВЕКТОРА Используя формулу (2):
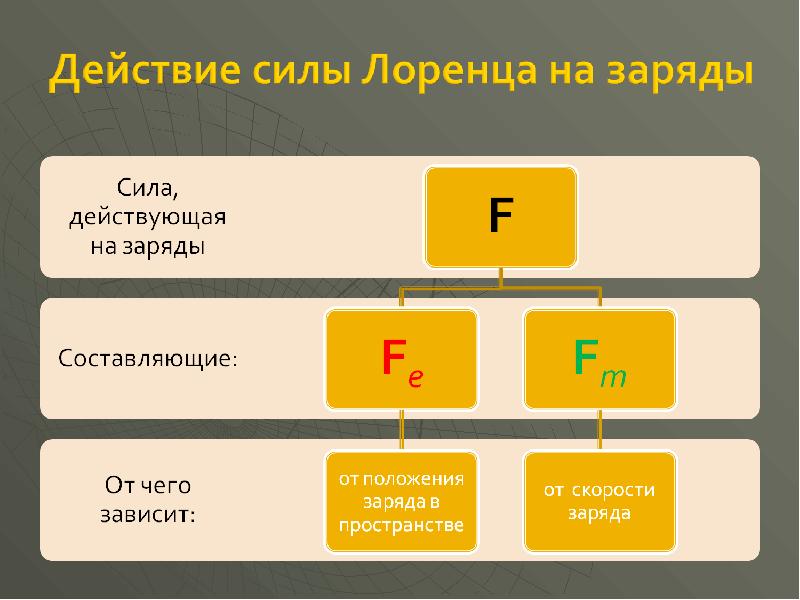
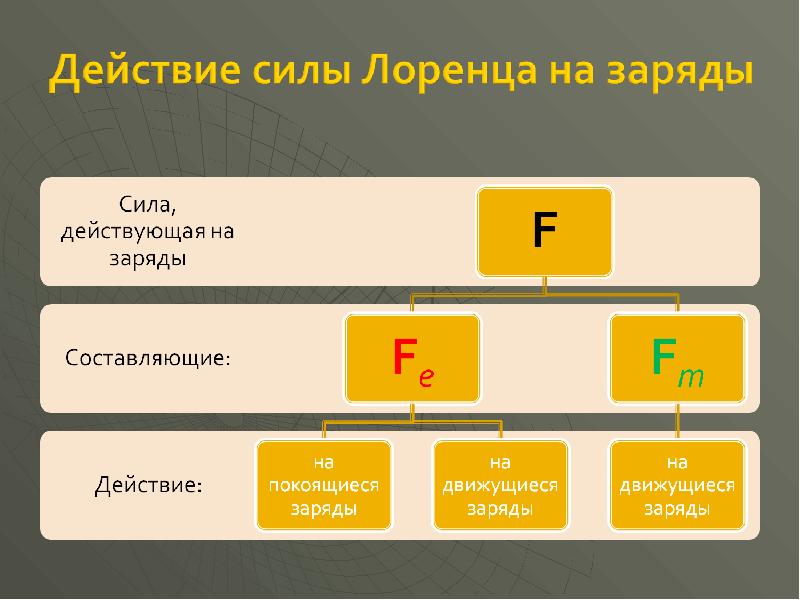
- 15. Опыт показывает, что сила F, действующая на точечный заряд q, в
- 17. Свойства магнитной составляющей можно описать, если ввести понятие магнитного поля. Если
- 19. Поле вектора B (магнитное поле): Поле вектора B (магнитное поле): не
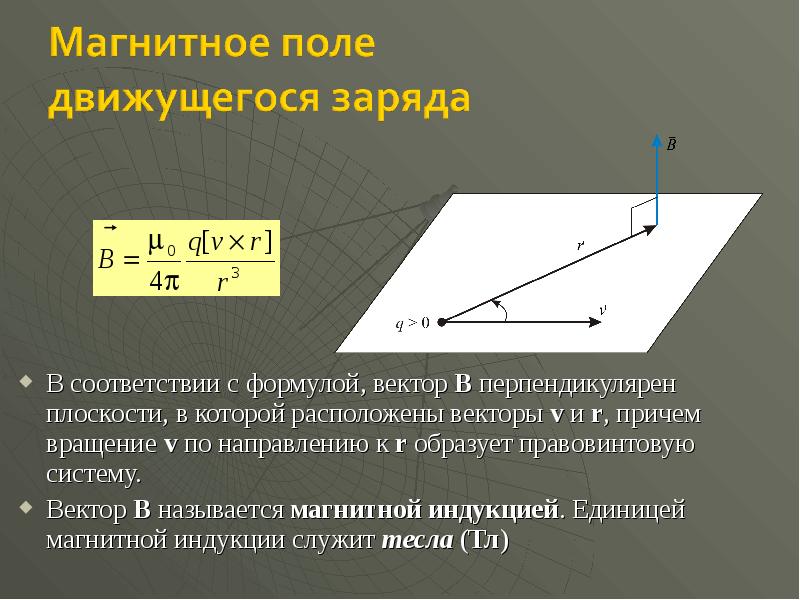
- 20. Опыт показывает, что само магнитное поле порождается движущимися зарядами (токами). Опыт
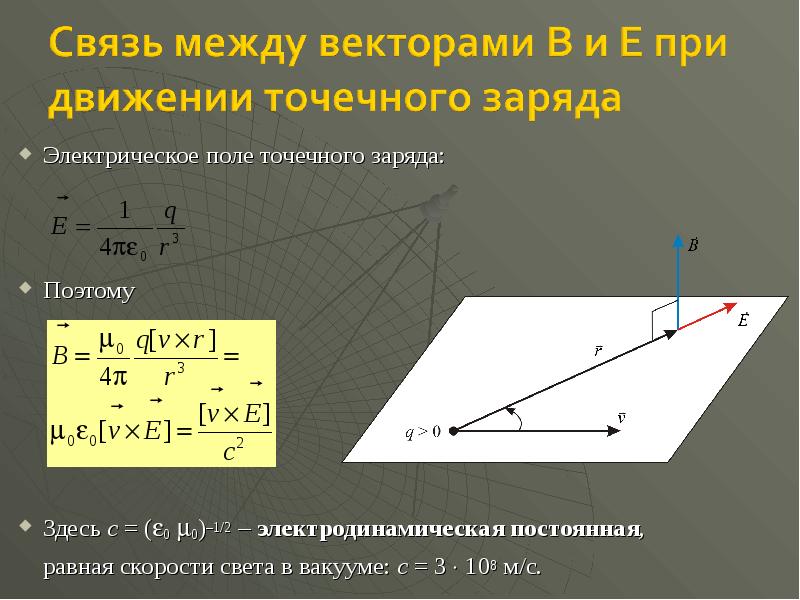
- 21. В соответствии с формулой, вектор B перпендикулярен плоскости, в которой расположены
- 22. Электрическое поле точечного заряда: Электрическое поле точечного заряда: Поэтому Здесь
- 23. Опыт показывает, что для магнитного поля, как и для электрического, справедлив
- 24. Рассмотрим вопрос о нахождении магнитного поля, создаваемого постоянными электрическими токами. Для
- 25. Если ток I течет по тонкому проводу с площадью поперечного сечения
- 26. Полное поле B в соответствии с принципом суперпозиции определяется в результате
- 27. Расчет по формулам закона Био – Свара – Лапласа магнитного поля
- 28. Найдем магнитную индукцию B в точке пространства, отстоящей на расстоянии b
- 29. Согласно закону Био – Савара – Лапласа, Согласно закону Био –
- 30. Из рисунка видно, что dlcos = rd, r = b/cos. Значит
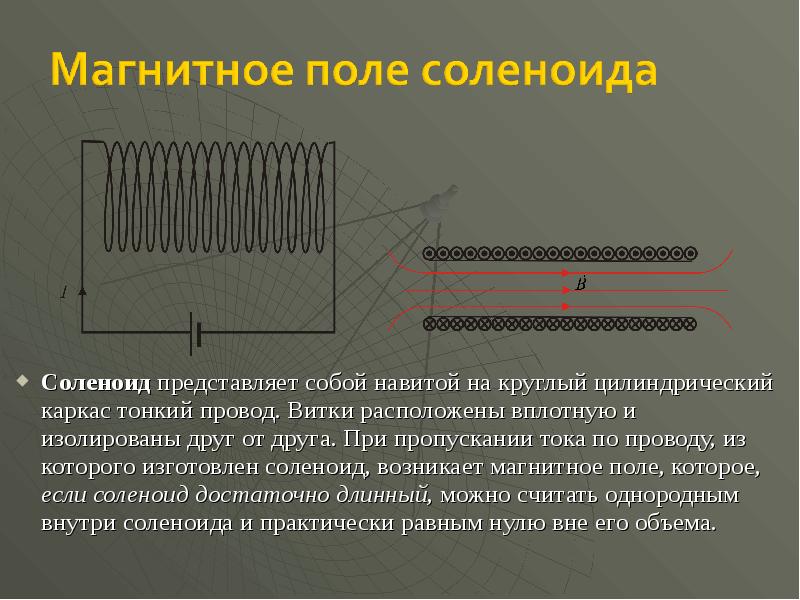
- 31. Соленоид представляет собой навитой на круглый цилиндрический каркас тонкий провод. Витки
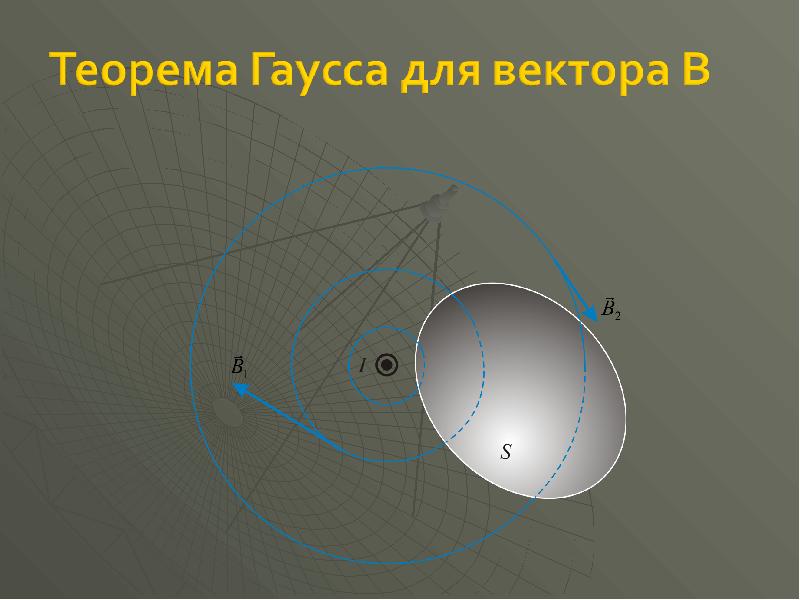
- 32. Теорема Гаусса для поля B. Поток вектора B сквозь любую замкнутую
- 33. Отсюда вытекает важное следствие: поток вектора B сквозь поверхность S ,
- 35. Теорема о циркуляции вектора B (для магнитного поля постоянных токов в
- 37. Заметим, что в электростатическом поле циркуляция вектора E равна нулю и
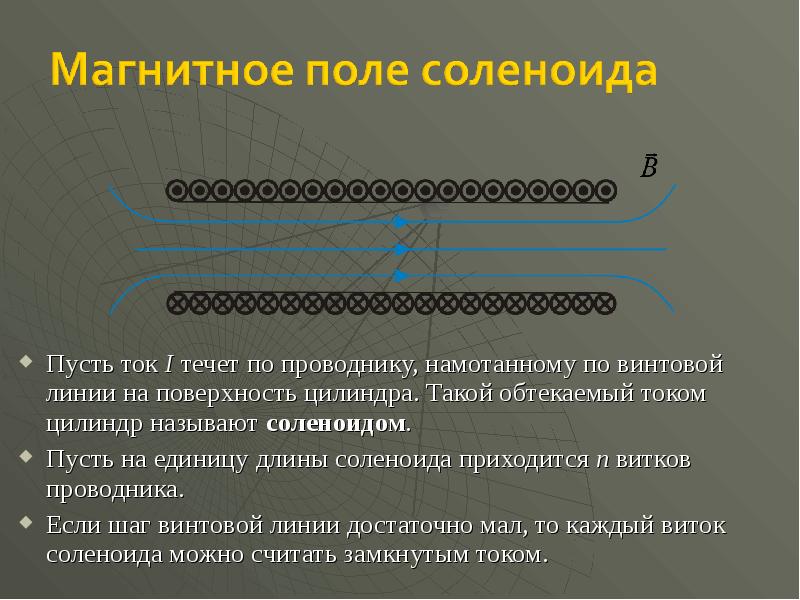
- 38. Пусть ток I течет по проводнику, намотанному по винтовой линии на
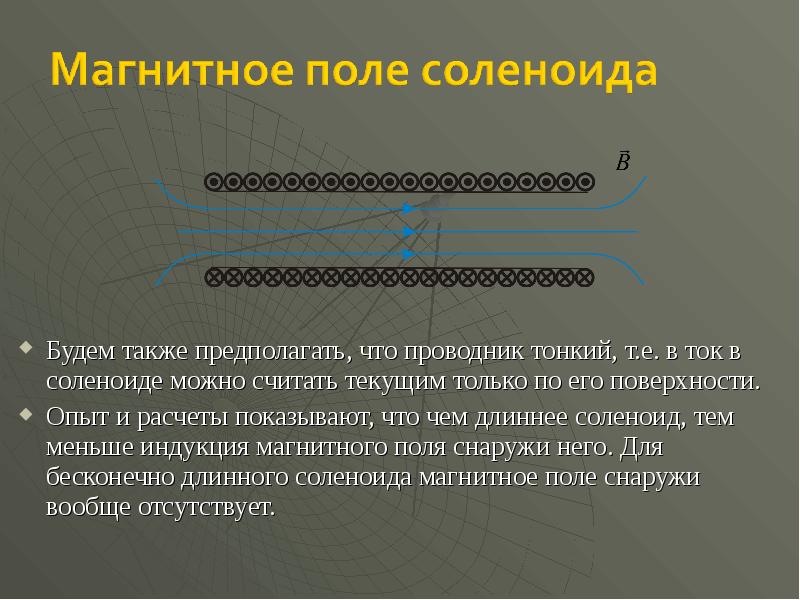
- 39. Будем также предполагать, что проводник тонкий, т.е. в ток в соленоиде
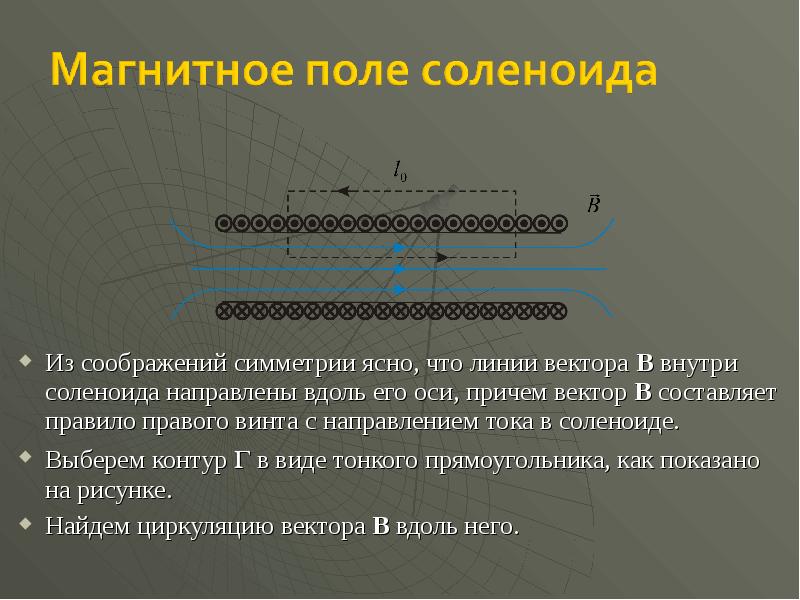
- 40. Из соображений симметрии ясно, что линии вектора B внутри соленоида направлены
- 41. Согласно теореме о циркуляции вектора B вдоль контура , имеем: Согласно
- 42. Каждый носитель тока испытывает действия магнитной силы Fm. Действие этой силы
- 43. Поскольку плотность тока в проводнике j = v и jdV =
- 44. Найдем амперову силу, с которой взаимодействуют в вакууме два бесконечно длинных
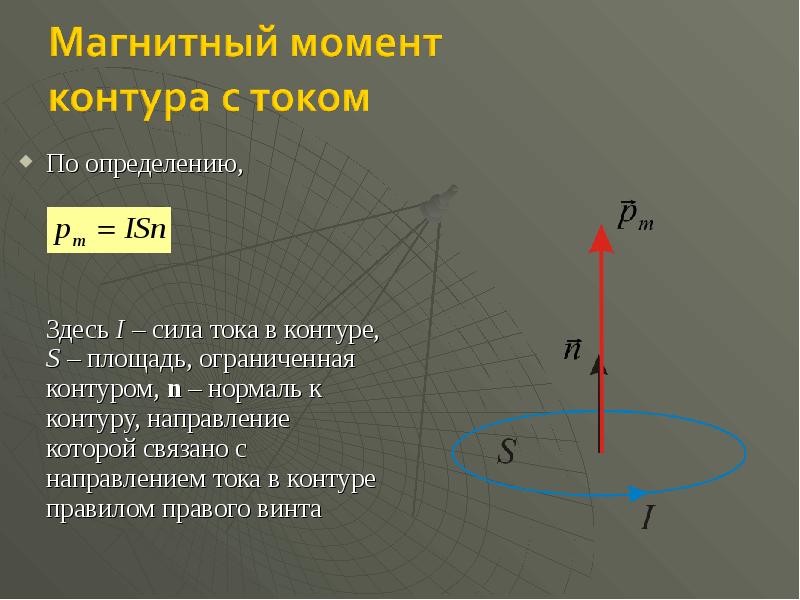
- 45. По определению, По определению, Здесь I – сила тока в контуре,
- 46. По определению, результирующий момент амперовых сил По определению, результирующий момент амперовых
- 47. Из приведенной формулы видно, что момент M амперовых сил, действующих на
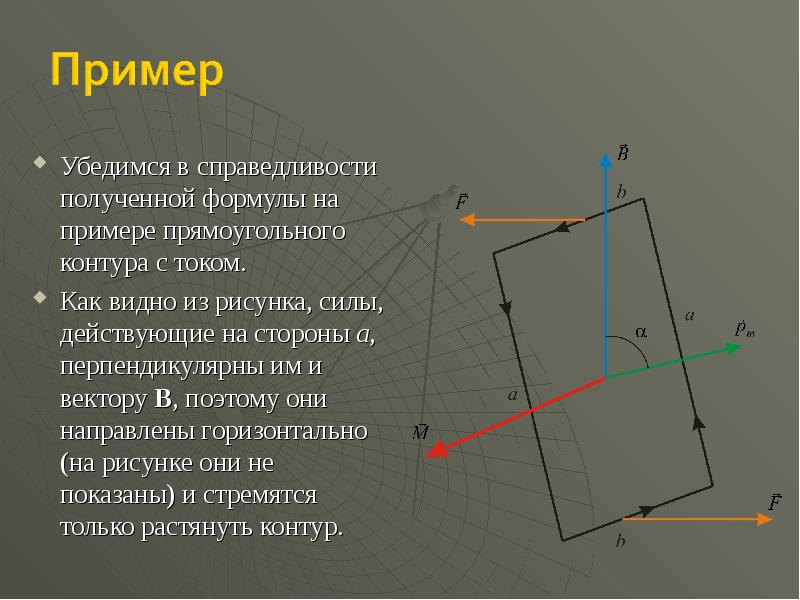
- 48. Убедимся в справедливости полученной формулы на примере прямоугольного контура с током.
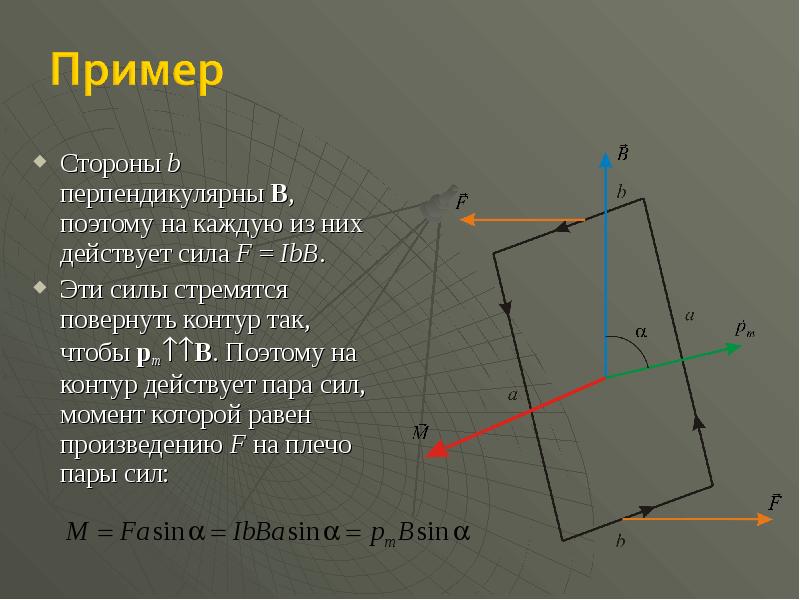
- 49. Стороны b перпендикулярны B, поэтому на каждую из них действует сила
- 50. Во внешнем неоднородном магнитном поле элементарный контур с током ведет себя
- 51. Когда контур с током находится во внешнем магнитном поле – мы
- 52. Скачать презентацию






































Слайды и текст этой презентации
Скачать презентацию на тему Экспериментальные факты, лежащие в основе теории магнетизма можно ниже:
Похожие презентации