Конвекция. Ламинарный тепловой погранслой при вынужденном движении жидкости вдоль плоской поверхности. (Тема 2. Лекции 8,9) презентация
Содержание
- 2. § 5. Ламинарный тепловой пограничный слой при вынужденном движении жидкости вдоль
- 3. 1) при y = 0 = 0 – очевидно; 1)
- 4. 1. Поток стационарен ∂T/∂t = 0 . 1. Поток
- 5. На поверхности пластины, т.е. при y = 0 u = 0
- 6. Таким образом, профиль избыточной температуры имеет приближенно следующий вид: Таким образом,
- 7. Подставляя значение производной избыточной температуры в формулу для , найдем Подставляя
- 8. Тогда формулу для коэффициента теплоотдачи можно переписать
- 9. Очевидно, что в рассматриваемом случае безграничной в направлении
- 10. где ,
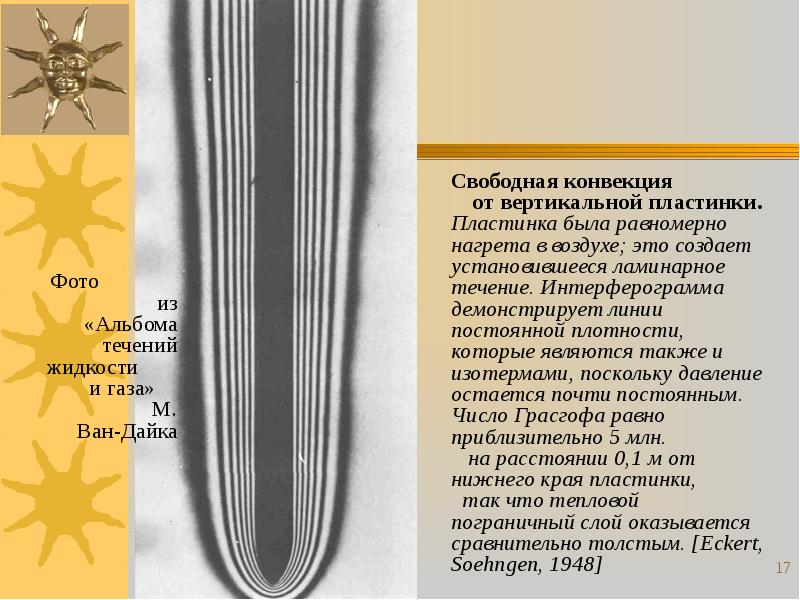
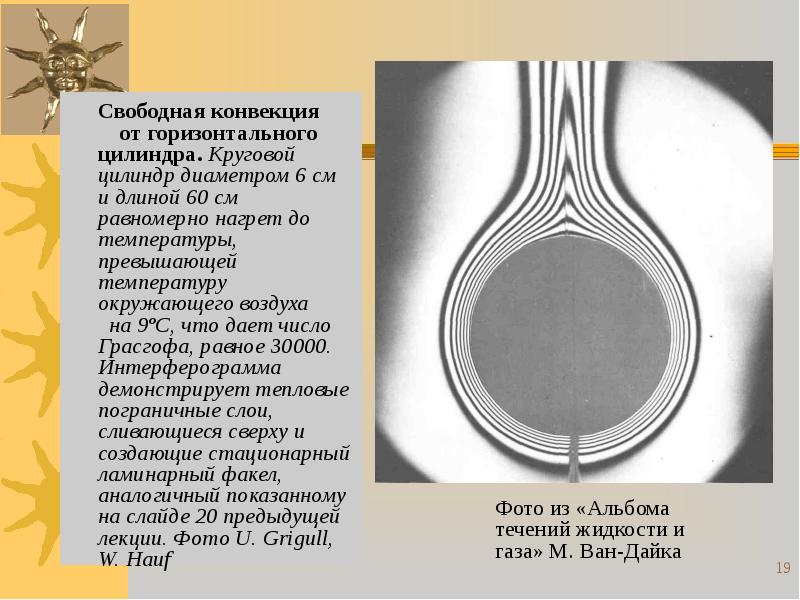
- 11. § 6. Конвективная теплоотдача при свободном
- 12. На элементарный объем dV, плотность среды в котором меньше плотности окружающей
- 13. Как это следует из уравнения Навье-Стокса, в частном случае одномерного стационарного
- 14. С учетом требования безразмерности величина, характеризующая соотношение архимедовой силы, сил инерции
- 15. Если изменение плотности обусловлено термическим расширением среды, критерий Архимеда принимает специфическую
- 16. Подставив выражение для в формулу для критерия Архимеда, получим: Подставив
- 22. Скачать презентацию



















Слайды и текст этой презентации
Скачать презентацию на тему Конвекция. Ламинарный тепловой погранслой при вынужденном движении жидкости вдоль плоской поверхности. (Тема 2. Лекции 8,9) можно ниже:
Похожие презентации