Механика упругих тел презентация

Лекция 10 Механика упругих тел

Деформации Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями.

Виды деформаций В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические. Упругими называются деформации, исчезающие после прекращения действия приложенных сил. Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. На пластических деформациях основана холодная обработка металлов – штамповка, ковка и пр.

Предел упругости Если сила не превосходит известной величины, называемой пределом упругости, то деформация будет упругой. Если же она превосходит этот предел, то возникающая деформация будет пластической. Предел упругости имеет различные значения для разных материалов. Он является не вполне четко определенной величиной. Разделение тел на упругие и пластические в какой-то степени условно. В некоторых случаях, например, можно пренебречь остаточными деформациями, если они не превосходят 0,1% от максимальных значений, достигавшихся под действием приложенных сил. В других случаях этот предел должен быть снижен до 0,01% и т.д.

Идеально упругое тело Тела мы будем считать идеально упругими. Так называются идеализированные тела, которые могут претерпевать только упругие, но не пластические деформации. Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями. В случае пластических деформаций такой однозначной связи не существует. Мы ограничимся изучением только малых деформаций. Малыми называются упругие деформации, подчиняющиеся закону Гука. Это – приближенный закон, согласно которому деформации пропорциональны силам, их вызывающим.

Изотропные и анизотропные тела Твердые тела разделяются на изотропные и анизотропные. Изотропными называются тела, свойства которых по всем направлениям одинаковы. Анизотропными называются тела, свойства которых в разных направлениях не одинаковы. Типичными представителями анизотропных тел являются кристаллы. В данной лекции мы ограничимся простейшим случаем, когда тела являются изотропными. Например, металлы обычно имеют поликристаллическую структуру, т.е. состоят из мельчайших беспорядочно ориентированных кристалликов. Каждый из таких кристалликов есть тело анизотропное. Но кусочек металла, содержащий множество их, ведет себя как изотропное тело, если всевозможные ориентации кристалликов представлены с одинаковой вероятностью.

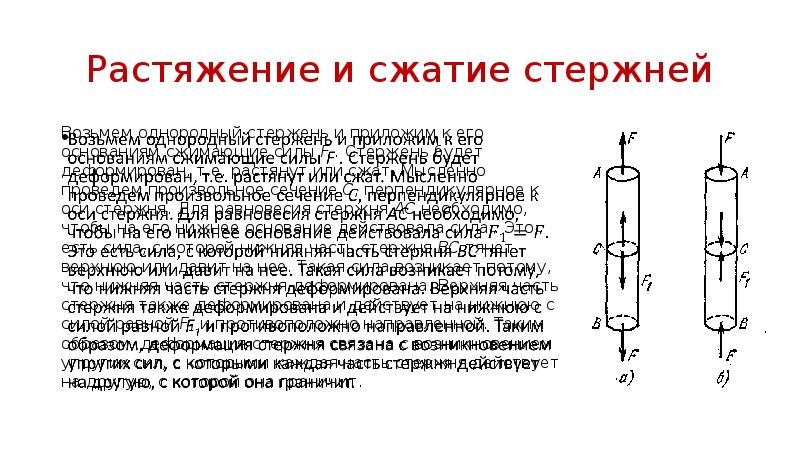
Растяжение и сжатие стержней Возьмем однородный стержень и приложим к его основаниям сжимающие силы F . Стержень будет деформирован, т.е. растянут или сжат. Мысленно проведем произвольное сечение C, перпендикулярное к оси стержня. Для равновесия стержня AC необходимо, чтобы на его нижнее основание действовала сила . Это есть сила, с которой нижняя часть стержня BC тянет верхнюю или давит на нее. Такая сила возникает потому, что нижняя часть стержня деформирована. Верхняя часть стержня также деформирована и действует на нижнюю с силой равной F1 и противоположно направленной. Таким образом, деформация стержня связана с возникновением упругих сил, с которыми каждая часть стержня действует на другую, с которой она граничит.

Растяжение и сжатие стержней . Если стержень растянут, то это напряжение называется натяжением и определяется выражением  ,   где S –площадь поперечного сечения стержня. Если же стержень сжат, то напряжение называется давлением и численно определяется той же формулой  .   Давление можно рассматривать как отрицательное натяжение и наоборот, т.е.  .  

Растяжение и сжатие стержней Пусть – длина недеформированного стержня. После приложения силы F его длина получает приращение и делается равной . Отношение    Называется относительным удлинением стержня. В случае растягивающих сил оно положительно, в случае сжимающих – отрицательно. По определению относительным сжатием называется величина . Она положительна в случае сжимающих сил и отрицательна – в случае отталкивающих.

Растяжение и сжатие стержней Опыт показывает, что для не слишком больших упругих деформаций натяжение T (или давление P) пропорциональны относительному удлинению (или относительному сжатию)     где E – постоянная, зависящая только от материала стержня т его физического состояния. Она называется модулем Юнга (1773 – 1829). Формулы выражают закон Гука (1635 – 1703). Это – приближенный закон. Для больших деформаций он может не выполняться. Деформации, для которых приближенно выполняется закон Гука, называются малыми деформациями.

Роберт Гук (Hook) (1635 – 1703) К числу открытий Гука принадлежат: открытие пропорциональности между упругими растяжениями, сжатиями и изгибами, и производящими их напряжениями (закон Гука), правильная формулировка закона всемирного тяготения (приоритет Гука оспаривался Ньютоном, но, по-видимому, не в части формулировки; кроме того, Ньютон утверждал о независимом и более раннем открытии этой формулы, которую, однако, до открытия Гуком никому не сообщал), открытие цветов тонких пленок (то есть, в конечном итоге, явления интерференции света), идея о волнообразном распространении света (более или менее одновременно с Гюйгенсом), экспериментальное обоснование её открытой Гуком интерференцией света, волновая теория света, гипотеза о поперечном характере световых волн, открытия в акустике, например, демонстрация того, что высота звука определяется частотой колебаний, теоретическое положение о сущности теплоты как движения частиц тела, открытие постоянства температуры таяния льда и кипения воды, закон Бойля (каков здесь вклад Гука, Бойля и его ученика Ричарда Таунли (Richard Townley) — не до конца ясно), живая клетка (с помощью усовершенствованного им микроскопа; Гуку же принадлежит сам термин «клетка» — англ. cell), непосредственное доказательство вращения Земли вокруг Солнца изменением параллакса звезды γ Дракона

Томас Юнг (1773 – 1829) В 1807 году в двухтомном труде «Курс лекций по натуральной философии и механическому искусству» Юнг обобщил результаты своих теоретических и экспериментальных работ по физической оптике (термин ввёл Юнг) и изложил свои исследования по деформации сдвига, ввёл числовую характеристику упругости при растяжении и сжатии — так называемый модуль Юнга. Он впервые рассмотрел механическую работу как величину, пропорциональную энергии (сам этот термин ввёл Юнг), под которой понимал величину, пропорциональную массе и квадрату скорости тела.

Растяжение и сжатие стержней Упругая энергия растянутого стержня. Приложим к стержню растягивающую силу f(x) и будем медленно увеличивать от начального значения f = 0 до конечного значения f = F. При этом удлинение стержня будет меняться от x = 0 до конечного значения x = l. По закону Гука , где k – коэффициент упругости, который легко выразить через модуль Юнга. Вся работа в рассматриваем процессе пойдет на приращение упругой энергии U, а потому   

Растяжение и сжатие стержней Опыт показывает, что под действием растягивающей или сжимающей силы F изменяются не только продольные, но и поперечные размеры стержня. Если сила F- растягивающая ,то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. Пусть a0 – толщина стержня до деформации, а – после деформации.. Если сила F растягивающая, то величина называется относительным поперечным сжатием стержня (). Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона  .   Коэффициент Пуассона зависит только от материала тела и является одной из важных постоянных, характеризующих его упругие свойства. Модуль Юнга E и коэффициент Пуассона  полностью характеризуют упругие свойства изотропного материала. Все прочие упругие постоянные могут быть выражены через E и .

Всестороннее растяжение и сжатие Допустим, что однородное изотропное тело имеет форму прямоугольного параллелепипеда, к противоположным граням которого приложены силы нормальные к этим граням. Соответствующие им натяжения обозначим . Определим деформации, которые возникнут под действием этих сил. Будем предполагать деформации малыми.

Всестороннее растяжение и сжатие Направим координатные оси параллельно ребрам параллелепипеда. Пусть x, y, z – длины этих ребер. Если бы действовала только сила Fx, то ребро x получило бы приращение , определяемое соотношением . Если бы действовала только сила Fy, то размеры параллелепипеда, перпендикулярные к оси Y, сократились бы. В частности, ребро x при этом получило бы отрицательное приращение , которое можно вычислить по формуле соотношением . Наконец, относительное приращение ребра x под действием одной только силы Fz, было бы равно . Если все силы действуют одновременно, то результирующее удлинение ребра x будет равно . Аналогично вычисляются удлинения параллелепипеда и вдоль остальных двух направлений Y и Z.

Всестороннее растяжение и сжатие В результате для удлинений всех трех ребер параллелепипеда можно написать   .

Всестороннее растяжение и сжатие Рассмотрим частный случай, когда все напряжения равны и отрицательны. В этом случае на параллелепипед со всех сторон действует постоянное давление . Как видно из формул все три относительные деформации равны между собой и определяются выражением  .   Их легко выразить через относительное изменение объема параллелепипеда при деформации. Действительно, взяв логарифмические производные от обеих частей равенства V = xyz, получим

Всестороннее растяжение и сжатие  .   Поэтому формулу можно представить в виде    где постоянная K определяется выражением  .   Эта постоянная называется модулем всестороннего сжатия.

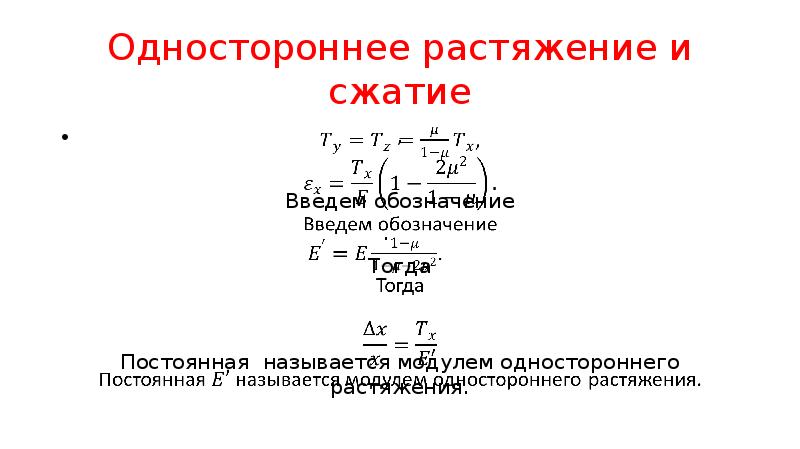
Одностороннее растяжение и сжатие Пусть однородный стержень может свободно растягиваться или сжиматься в направлении его оси (которую мы примем за координатную ось X), а его поперечные размеры изменяться не могут. Поперечные натяжения и найдутся из условия неизменности размеров стержня в направлениях Y и Z. Полагая в формулах , получим  

Одностороннее растяжение и сжатие , Введем обозначение .   Тогда Постоянная называется модулем одностороннего растяжения.

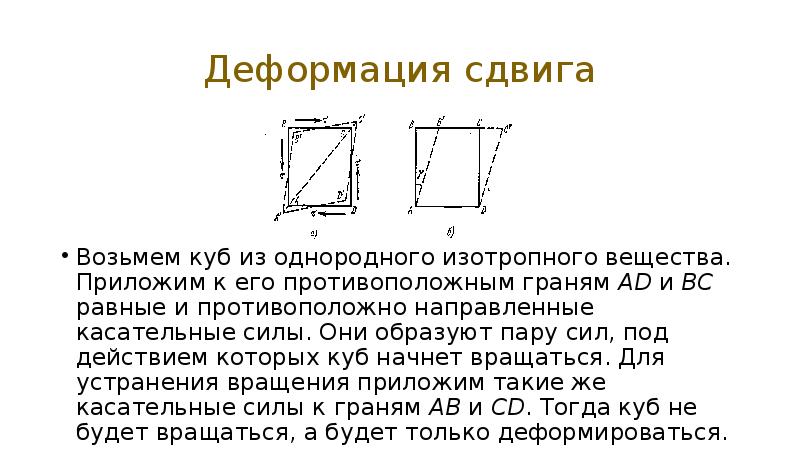
Деформация сдвига Возьмем куб из однородного изотропного вещества. Приложим к его противоположным граням AD и BC равные и противоположно направленные касательные силы. Они образуют пару сил, под действием которых куб начнет вращаться. Для устранения вращения приложим такие же касательные силы к граням AB и CD. Тогда куб не будет вращаться, а будет только деформироваться.

Деформация сдвига Опыт показывает, что под действием приложенных напряжений квадрат ABCD переходит в ромб . При этом длина диагонали AC увеличивается, а длина диагонали BD уменьшается. Объем тела при такой деформации практически не меняется. Поэтому куб после деформации можно повернуть так, чтобы новое основание совместилось с прежним основанием AD. Отсюда видно, что рассматриваемая деформация состоит в том, что все слои куба, параллельные основанию AD, сдвигаются в одном и том же направлении, параллельном тому же основанию. Поэтому эта деформация называется сдвигом. Величина сдвига пропорциональна расстоянию сдвигаемого слоя от основания AD. Угол γ между гранью AB до и той же гранью после деформации называется углом сдвига

Деформация сдвига Мы предполагаем, что угол γ мал (γ<<1) и пользуемся законом Гука. Для деформации сдвига этот закон можно записать в виде  ,   где  - касательное напряжение, действующее на гранях куба. Постоянная G называется модулем сдвига и зависит от материала, из которого изготовлен куб. В теории упругих деформаций показывается, что  . Эта формула устанавливает связь между модулем Юнга E, коэффициентом Пуассона  и модулем сдвига G.

Деформации кручения Возьмем стержень в виде кругового цилиндра, длиной L и радиусом r. Пусть верхнее сечение стержня закреплено неподвижно, а к нижнему приложен момент силы, закручивающий стержень. Введем в рассмотрение отрезок OA = , отложенный вдоль одного из радиусов нижнего сечения. Под влиянием закручивающего момента отрезок OA повернется на угол  и займет положение . Относительной деформацией будет величина , т.е. угол закручивания, отнесенный к единице длины стержня. В пределах упругой деформации эта величина пропорциональна закручивающему моменту M:    Величина c постоянна для данного стержня. Для определения c свяжем деформацию кручения с деформацией сдвига.

Деформации кручения При закручивании стержня его нижний торец испытывает сдвиг относительно верхнего; прямая BA поворачивается, принимая положение , угол  является углом сдвига. Этот угол равен  ,   где  - касательное усилие, приложенное к элементу поверхности dS, расположенному у точки а G – модуль сдвига.

Деформации кручения Угол   откуда   .   Сила, приложенная к элементу поверхности dS, равна dS, а ее момент . Вводя полярные координаты и , получим для элемента поверхности

Деформации кручения . Подставляя сюда значение  , найдем . Полный момент M, приложенный ко всему нижнему торцу стержня, получим, проинтегрировав это выражение по всей площади круга радиуса r: откуда получаем   .

Деформации кручения Отсюда Угол закручивания  зависит от модуля сдвига G и обратно пропорционален радиусу стержня, взятому в четвертой степени.     Имеем, что для закручивания проволоки на данный угол  надо приложить момент M, прямо пропорциональный r4 и обратно пропорциональный длине проволоки L.

Деформации кручения Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания тяжелого тела, подвешенного к нижнему концу проволоки. Эти колебания будут гармоническими с периодом   Если момент инерции тела известен, то, измеряя период колебаний, можно вычислить по этой формуле модуль кручения M.

Деформации изгиба Рассмотрим изгиб однородного бруса произвольного поперечного сечения. Проведя сечения AB и , нормальные к оси бруса, мысленно вырежем из него бесконечно малый элемент длину которого обозначим l0. Прямые и все прямые, им параллельные, перейдут в окружности с центрами, лежащими на оси O, перпендикулярной к плоскости рисунка Эта ось называется осью изгиба. Наружные волокна, лежащие выше линии , при изгибе удлиняются, волокна, лежащие ниже линии , - укорачиваются. Длина линии остается неизменной. Эта линия называется нейтральной линией.

Деформации изгиба Все наружные волокна будут натянуты, все внутренние – сжаты. Пусть R – радиус кривизны нейтральной линии . Тогда , где α – центральный угол, опирающийся на дугу . Рассмотрим волокно бруса, находящееся на расстоянии  от нейтрального сечения. (Величина  положительна, если волокно находится выше нейтрального сечения и отрицательна, если оно находится ниже). Если брус не слишком толст, так что , то длина рассматриваемого волокна будет , а удлинение . Следовательно, натяжение, действующее вдоль рассматриваемого волокна , или  .

Деформации изгиба Натяжение, таким образом, меняется линейно с расстоянием . Мы будем считать, что сумма всех сил натяжения, действующих в каждом нормальном сечении бруса, равна нулю, т.е. , где dS – элемент площади рассматриваемого поперечного сечения. Интегрирование ведется по всему поперечному сечению бруса. Отсюда видно, что нейтральная линия и нейтральное сечение проходят через центр масс поперечного сечения бруса. Из соотношения следует, что момент сил натяжения M, действующий на сечение AB, не зависит от того, относительно какой оси он берется.

Деформации изгиба Для вычисления M проще всего взять ось, перпендикулярную к плоскости рисунка и проходящую через точку N. Очевидно,  , или где введено обозначение .   Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако, в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, это чисто геометрическая величина с размерностью четвертой степени длины.

Распространение продольных упругих возмущений Если в каком-либо месте упругой среды возникла деформация, то по прекращении внешних воздействий она не остается на месте, а распространяется в среде во всех направлениях. В таких случаях говорят о распространении в среде упругих возмущений или волн. Примерами могут служить звуковые волны в твердых телах, жидкостях или газах.

Распространение продольных упругих возмущений Пусть имеется прямолинейный ряд, состоящий из одинаковых твердых идеально упругих шаров, соприкасающихся между собой. Ряд таких шаров неограниченно простирается вправо. Нанеся удар по первому шару, сообщим ему некоторую скорость . Первый шар ударится о второй. При упругом ударе шары просто обмениваются скоростями: первый шар остановится, а второй придет в движение с той же скоростью . Движение будет передаваться от шара к шару. В результате возникнет возмущение, распространяющееся вдоль ряда шаров. Скорость распространения такого возмущения обозначим c. Ее нельзя смешивать со скоростью того шара, который в рассматриваемый момент движется.

Распространение продольных упругих возмущений Изменим теперь постановку опыта. В тот момент, когда при столкновении со вторым шаром первый шар остановится, нанесем по нему второй удар, чтобы он приобрел прежнюю скорость . Тогда в этот момент первые два шара будут иметь одну и ту же общую скорость . Затем при ударе о третий шар второй шар передаст ему свою скорость, а сам остановится. Первый шар при столкновении со вторым сделает то же самое. В результате движение перейдет от первых двух шаров ко второму и третьему. Затем оно будет передано третьему и четвертому шару. Короче говоря, вдоль ряда побежит возмущение, в котором в каждый момент движутся два шара, соприкасающиеся между собой, а остальные покоятся.

Распространение продольных упругих возмущений Допустим теперь, что всякий раз, как первый шар передает свое движение второму шару, он получает удар, в результате которого его скорость восстанавливается. Состояние движения представлено на рис. в. Все шары, расположенные левее некоторой границы, движутся со скоростью , а шары, расположенные правее этой границы, находятся в состоянии покоя. Сама граница перемещается вправо со скоростью c, так что в движение вовлекаются все новые и новые шары.

Распространение продольных упругих возмущений Очевидно, ничто не изменится, если вместо шаров взять прямолинейный ряд, состоящий из упругих цилиндров, соприкасающихся между собой своими основаниями. Это замечание позволяет легко выполнить предельный переход к сплошной среде.

Распространение продольных упругих возмущений Допустим, что длины цилиндров неограниченно уменьшаются, а число их неограниченно растет. Вместе с тем удары, которым подвергается первый цилиндр, становятся все чаще и чаще, а сила каждого удара – все слабее и слабее. В пределе получится сплошной стержень, на свободный конец которого действует постоянная сила F. Вещество стержня, находящееся левее некоторой границы B, движется с постоянной одной и той же скоростью , а вещество правее границы находится в покое. Сама граница B перемещается вправо с постоянной скоростью с. В акустике, как правило, имеют дело с так называемыми малыми возмущениями. В этих случаях скорость вещества бывает очень мала по сравнению со скоростью распространения возмущения c.

Распространение продольных упругих возмущений Вычислим скорость распространения малых продольных возмущений в стержне, возникших в результате действия постоянной силы давления F, приложенной в некоторый момент к его свободному концу. Этот момент в дальнейшем принимается за нулевой, т.е. за начало отсчета времени. В возмущенной области стержня все вещество в любой момент времени t движется с постоянной скоростью , а сам стержень в указанной области всюду деформирован одинаково. Если m – масса деформированной части стержня, в момент t, то его импульс в тот же момент будет . Приращение импульса стержня за время dt, т.е. равно импульсу силы за то же время. Это дает   .

Распространение продольных упругих возмущений За время t возмущение проходит путь , так что масса возмущенной области стержня будет , где S – площадь поперечного сечения стержня а  - его плотность. Подставив в формулу , , где P – давление в возмущенной области стержня, получим  .   Давление P связано с относительным сжатием стержня соотношением . Для нахождения  заметим, что к моменту времени t правый конец сжатой области стержня B еще не успел переместиться, тогда как левый свободный конец его двигался в течение времени t и переместился на расстояние . В результате длина возмущенной области стержня по сравнению со своей исходной длиной укоротится на . Поэтому  ,  .  Исключая P из формул, получим 

Распространение продольных упругих возмущений . Этой формулой определяется скорость распространения упругих волн в стержне.

Распространение продольных возмущений в неограниченной среде Возмущения в стержне, рассмотренные в разделе (10.7) мы назвали продольными. Это не совсем точно. Каждая деформация сжатия стержня сопровождается увеличением поперечных размеров его. В случае деформации растяжения поперечные размеры стержня сокращаются. Для количественного описания этих явлений был введен коэффициент Пуассона. Следовательно, частицы в стержне движутся не совсем параллельно его оси: наряду с продольной они имеют и поперечную составляющую. Чтобы сделать возмущение чисто продольным, надо лишить частицы стержня возможности перемещаться в поперечных направлениях, т.е. «закрепить» боковую поверхность стержня. Такой случай осуществляется в неограниченной среде при распространении в ней продольных возмущений. Если в такой среде мысленно вырезать произвольный «стержень» с осью, параллельной направлению распространения (которое в случае продольных возмущений параллельно смещениям частиц), то частицы, находящиеся на боковой поверхности его, не будут претерпевать никаких боковых смещений. Все смещения будут происходить только параллельно оси «стержня».

Распространение продольных возмущений в неограниченной среде Надо модуль Юнга E заменить модулем всестороннего растяжения . В результате для скорости распространения продольных возмущений в неограниченной среде получится выражение     Или   .

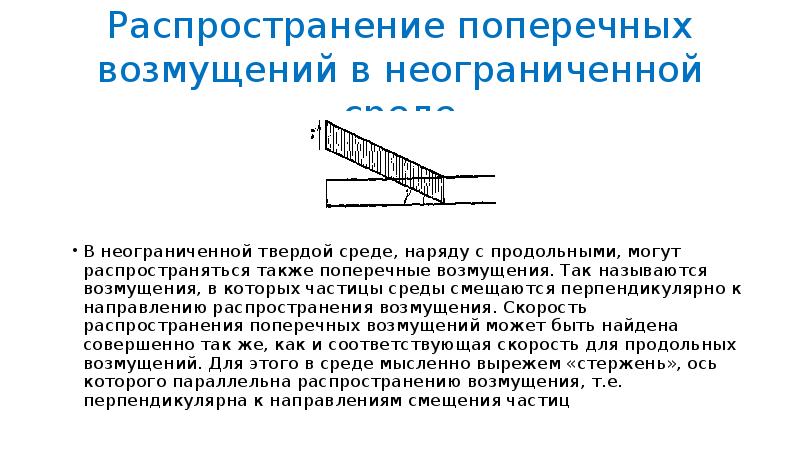
Распространение поперечных возмущений в неограниченной среде В неограниченной твердой среде, наряду с продольными, могут распространяться также поперечные возмущения. Так называются возмущения, в которых частицы среды смещаются перпендикулярно к направлению распространения возмущения. Скорость распространения поперечных возмущений может быть найдена совершенно так же, как и соответствующая скорость для продольных возмущений. Для этого в среде мысленно вырежем «стержень», ось которого параллельна распространению возмущения, т.е. перпендикулярна к направлениям смещения частиц

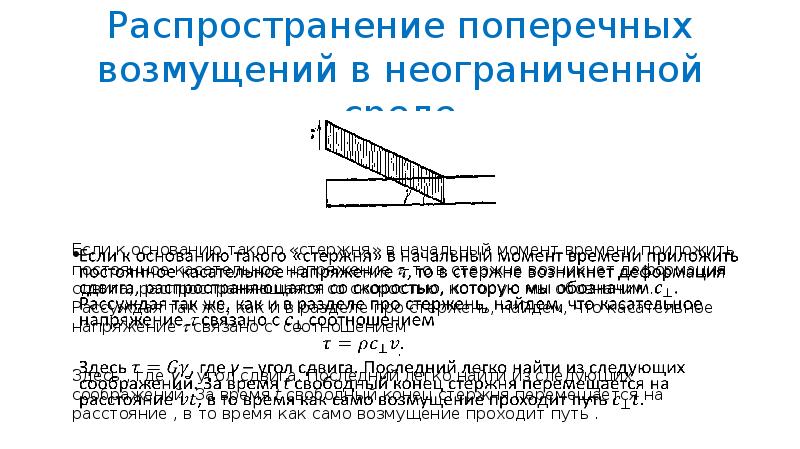
Распространение поперечных возмущений в неограниченной среде Если к основанию такого «стержня» в начальный момент времени приложить постоянное касательное напряжение , то в стержне возникнет деформация сдвига, распространяющаяся со скоростью, которую мы обозначим . Рассуждая так же, как и в разделе про стержень, найдем, что касательное напряжение  связано с соотношением .   Здесь , где γ – угол сдвига. Последний легко найти из следующих соображений. За время t свободный конец стержня перемещается на расстояние , в то время как само возмущение проходит путь .

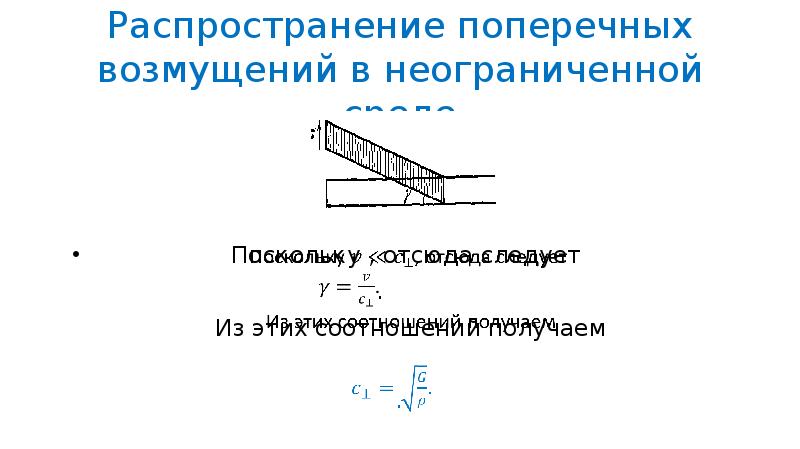
Распространение поперечных возмущений в неограниченной среде Поскольку , отсюда следует  .   Из этих соотношений получаем   .

Поперечные возмущения в натянутом шнуре  Возможность распространения поперечных возмущений в твердых телах обусловлена присущей им поперечной упругостью, т.е. способностью сопротивляться всякому изменению формы, происходящему без изменения объема. Поперечная упругость может быть создана искусственно и в случае таких тел, у которых в естественном состоянии она отсутствует. Если же закрепить один конец шнура, а к другому подвесить груз, перекинув шнур через блок, то в шнуре возникнет постоянное напряжение, обозначаемое в дальнейшем T. Такой шнур обладает упругостью формы, и в нем могут распространяться поперечные возмущения. Скорость таких возмущений может быть рассчитана по формуле . Но для этого надо решить вопрос, какая величина в натянутом шнуре играет роль модуля сдвига G.

Поперечные возмущения в натянутом шнуре Рассмотрим небольшой участок натянутого шнура. Будем предполагать, что деформации натянутого шнура, связанные с поперечными смещениями его частиц, малы. Тогда можно пренебречь изменениями величины натяжения шнура при таких малых деформациях. В этом приближении натяжения T, действующие на концы участка AB вдоль его оси, одни и те же. Их составляющие, касательные к основаниям участка AB, равны .

Поперечные возмущения в натянутом шнуре Поэтому на основаниях рассматриваемого участка будут действовать касательные напряжения , где S – площадь поперечного сечения шнура. Деформацию участка AB можно рассматривать как сдвиг под действием таких касательных напряжений. Сравнивая предыдущее выражение с формулой , находим, что роль модуля сдвига играет величина .  .   Величина равна массе, приходящейся на единицу длины шнура. Она называется линейной плотностью шнура.

До следующей лекции