Основы зонной теории твердого тела презентация
Содержание
- 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА Энергетический спектр электрона в изолированном атоме
- 3. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА При объединении атомов в кристалл значение
- 4. Трансляционная симметрия в кристаллах Важные свойства электрона, позволяющие построить теорию
- 5. «Потенциальная яма»
- 6. Под влиянием внешних факторов (света, температуры и т.д.) электрон может увеличить
- 7. «Освобождение» электрона
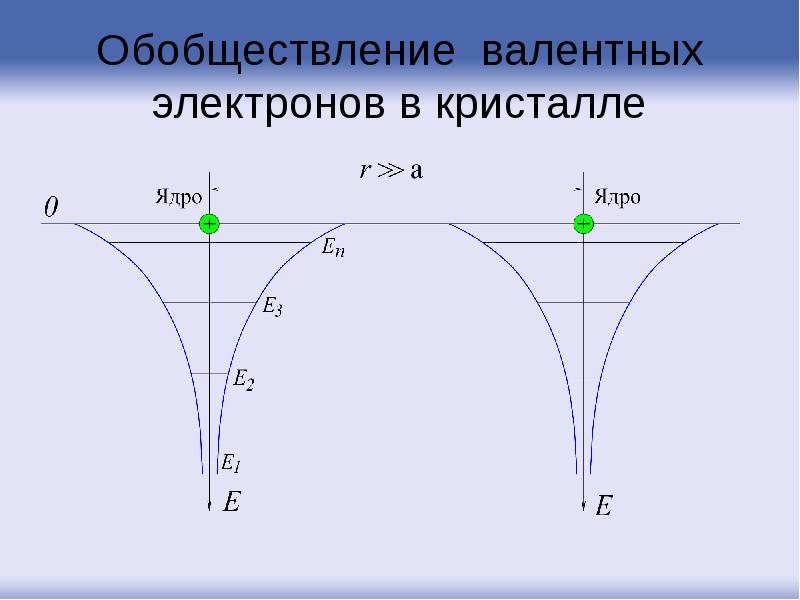
- 8. При сближении атомов потенциальные кривые частично налагаются друг на друга и
- 9. Обобществление валентных электронов в кристалле
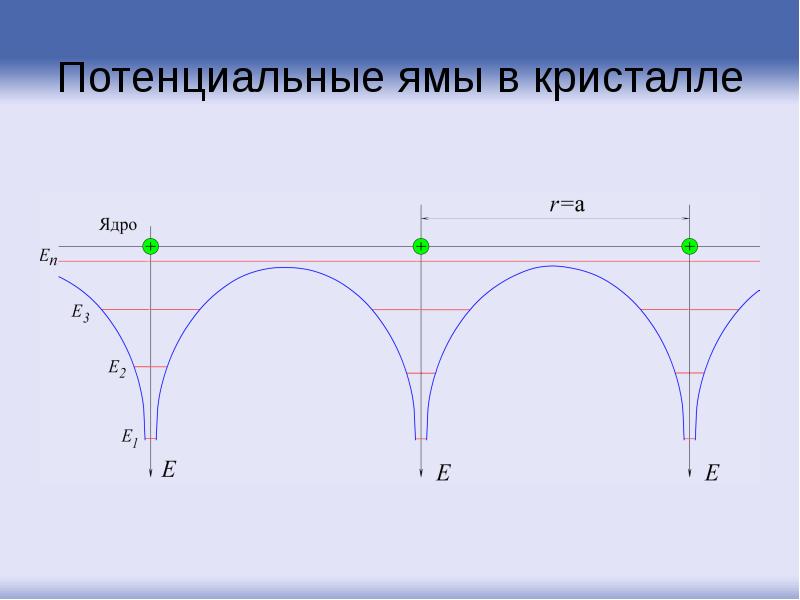
- 10. Потенциальные ямы в кристалле
- 11. До тех пор, пока электрон будет находиться в кристалле, он будет
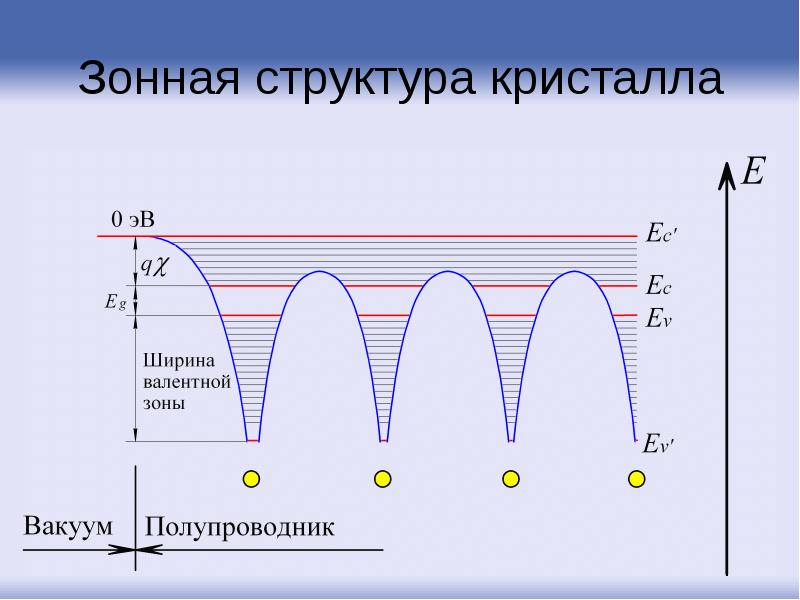
- 12. Зонная структура кристалла
- 13. свободный электронный газ Для металлов и полупроводников вводят понятие свободный
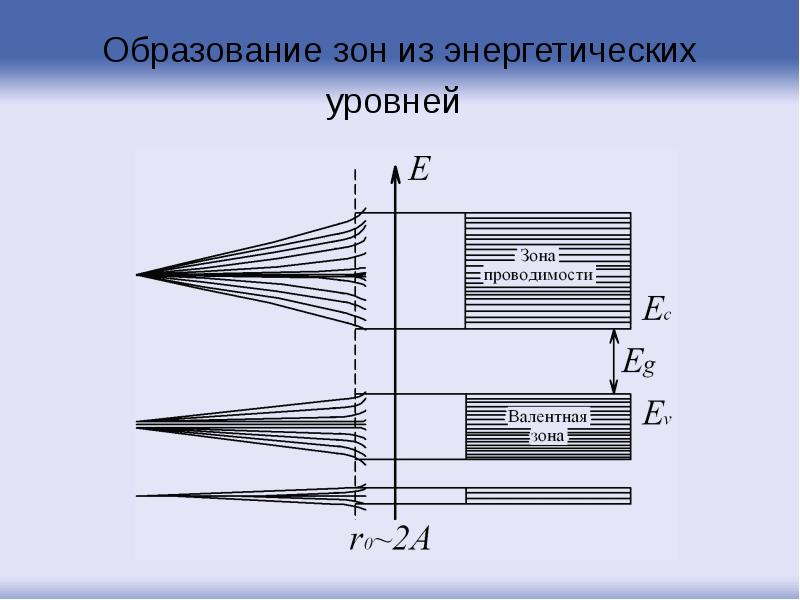
- 14. Образование зон из энергетических уровней
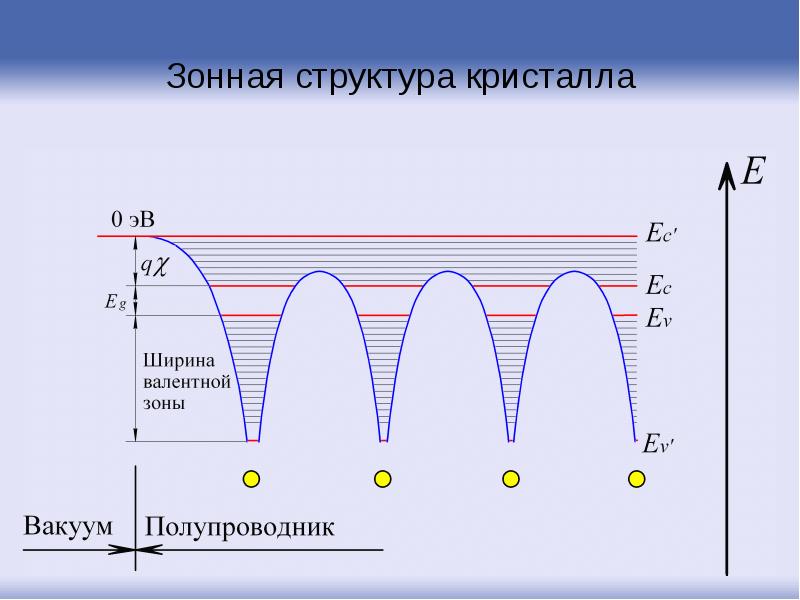
- 15. Зонная структура кристалла
- 16. Потенциальная энергия электрона
- 17. Граничные условия Борна – Кармана Периодическое (циклическое) изменение потенциальной энергии накладывает
- 19. Уравнение Шредингера для частицы (электрона) в периодической решетке:
- 20. Браве (Bravais) Огюст (1811—1863)
- 21. Что такое решетка Бравэ? Решетка Браве (названа в честь французского физика
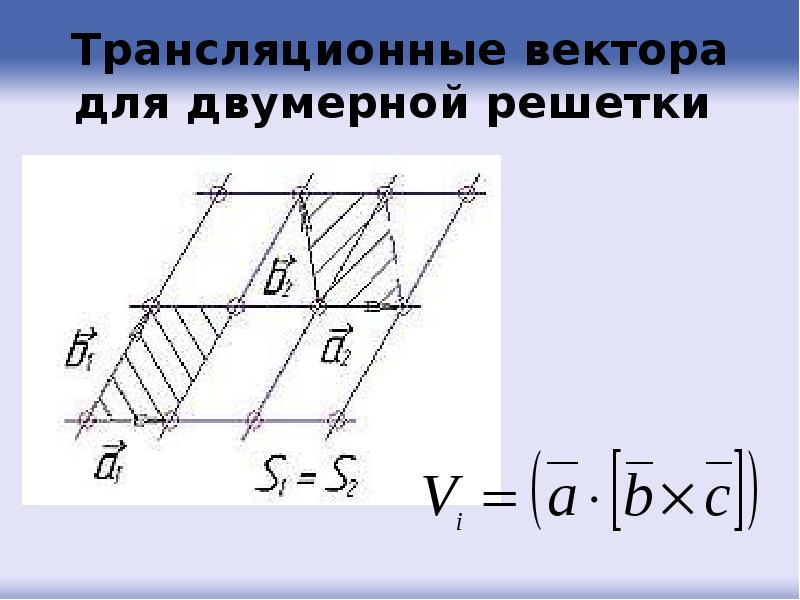
- 22. Трансляционные вектора для двумерной решетки
- 23. Решеткой или системой трансляций Браве называется набор элементарных трансляций или трансляционная
- 24. Элементарная ячейка решетки Браве – параллелепипед, построенный на основных векторах трансляции.
- 25. Основным трансляционным вектором называется минимальный в данном направлении вектор перехода из
- 26. Элементарные ячейки, содержащие частицы только в вершинах, называют простыми, или примитивными.
- 27. Базисом ячейки называют совокупность координат узлов, приходящихся на элементарную ячейку. Так
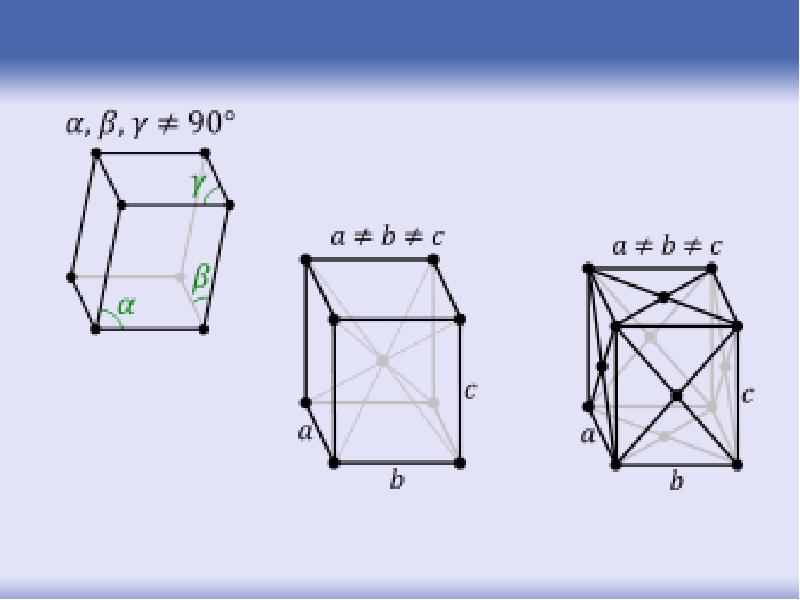
- 28. Типы решеток Браве Четырнадцать трехмерных решеток Браве обычно подразделяются на
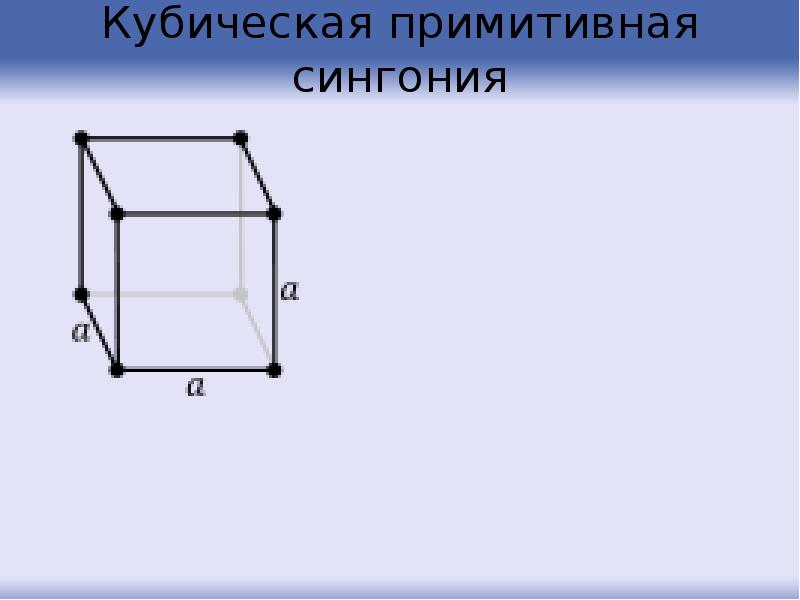
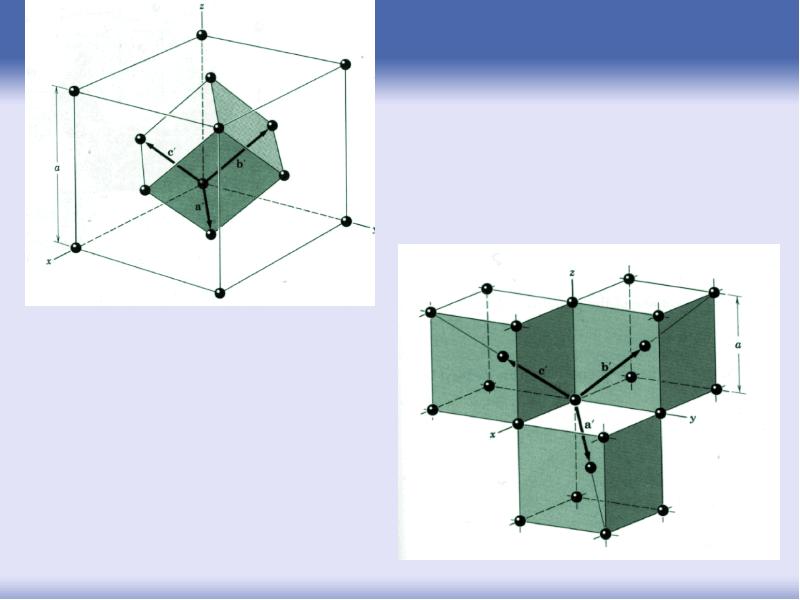
- 29. Кубическая примитивная сингония
- 31. кристаллографические плоскости и индексы Миллера Через узлы решетки можно провести
- 32. Индексы Миллера Пусть одна из плоскостей отсекает на осях координат отрезки
- 33. Индексы Миллера
- 34. Индексы Миллера Целые числа h, k, l, обратно пропорциональные отрезкам, которые
- 35. Индексы Миллера Индексы Миллера находятся следующим образом: Определяются координаты (х, у,
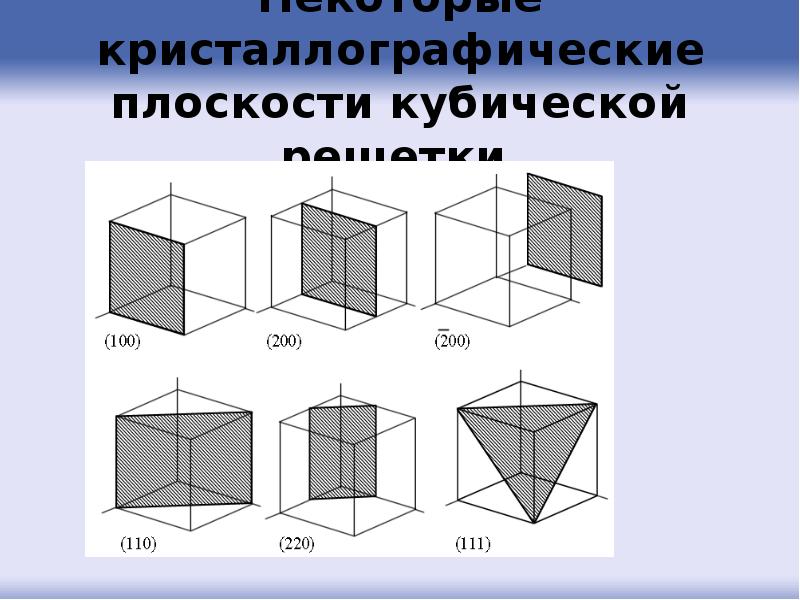
- 36. Некоторые кристаллографические плоскости кубической решетки
- 37. Заметим, что параллельно изображенной плоскости можно провести много параллельных плоскостей, проходящих
- 38. По аналогии с прямой кристаллической решеткой можно построить обратную решетку, широко
- 39. координатные оси и единичные вектора выбираются следующим образом
- 40. Вектор перпендикулярен векторам и∙ следовательно, является нормалью к
- 41. Теорема Блоха Рассмотрим идеальный бесконечный кристалл, т.е. кристалл, в котором отсутствуют
- 42. Феликс Блох лауреат Нобелевской премии по физике
- 43. Теорема Блоха устанавливает вид волновой функции частицы, находящейся в периодическом
- 44. – периодическое поле кристаллической решетки по всем векторам r решетки Бравэ,
- 45. В иной записи теорема Блоха имеет вид Согласно теореме Блоха,
- 46. Соответствующие им собственные значения энергии En( )=En( +
- 47. Так как собственные значения энергии при заданном n, периодичны по ,
- 48. Иными словами, обладает свойством трехмерной периодичности кристалла. Такую функцию можно разложить
- 49. Действительная часть комплексной экспоненты Действительная часть комплексной экспоненты где
- 50. Плоская волна удовлетворяет условиям Борна – Кармана только при
- 51. Иными словами, на длине L должно укладываться целое число длин волн:
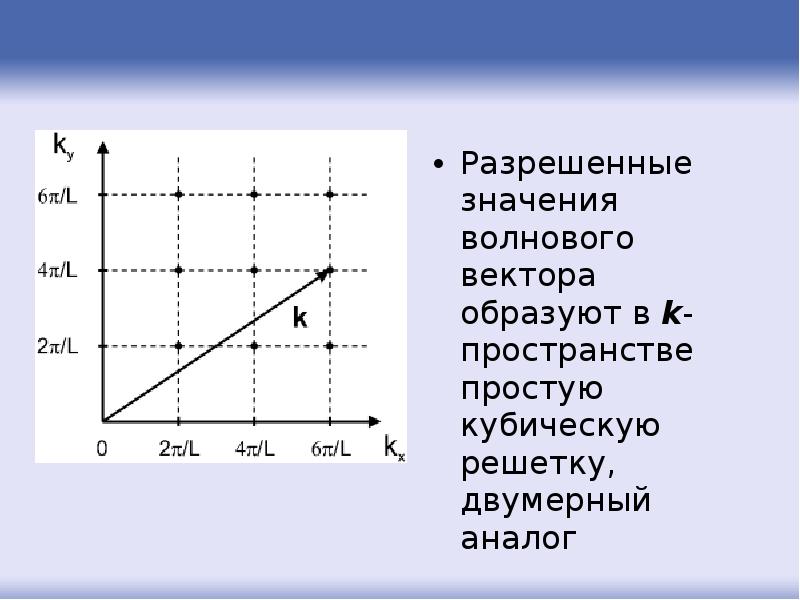
- 52. Разрешенные значения волнового вектора образуют в k-пространстве простую кубическую решетку, двумерный
- 53. Рассмотрим идеальный бесконечный кристалл, т.е. кристалл, в котором отсутствуют дефекты, и
- 54. В элементе объема обратного пространства Δ3k содержится
- 55. Вектор определяет узлы обратной решетки Вектор определяет узлы
- 56. Используя определение векторов , Используя определение
- 57. Из трансляционного условия, накладываемого на волновую функцию электрона, движущегося в поле
- 58. Таким образом, уравнение Шредингера для свободной частицы имеет вид Таким
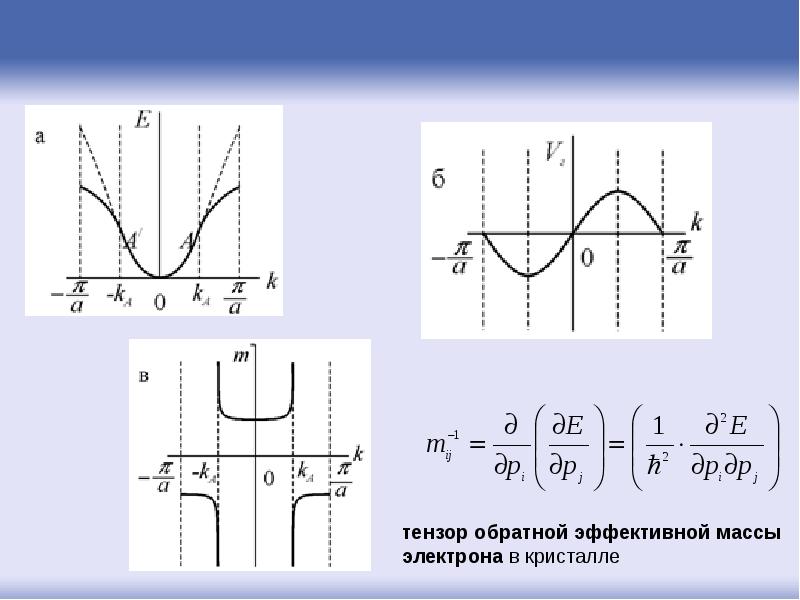
- 59. Эффективная масса электрона
- 60. Зоны Бриллюэна Пространство (или ) можно разбить на области
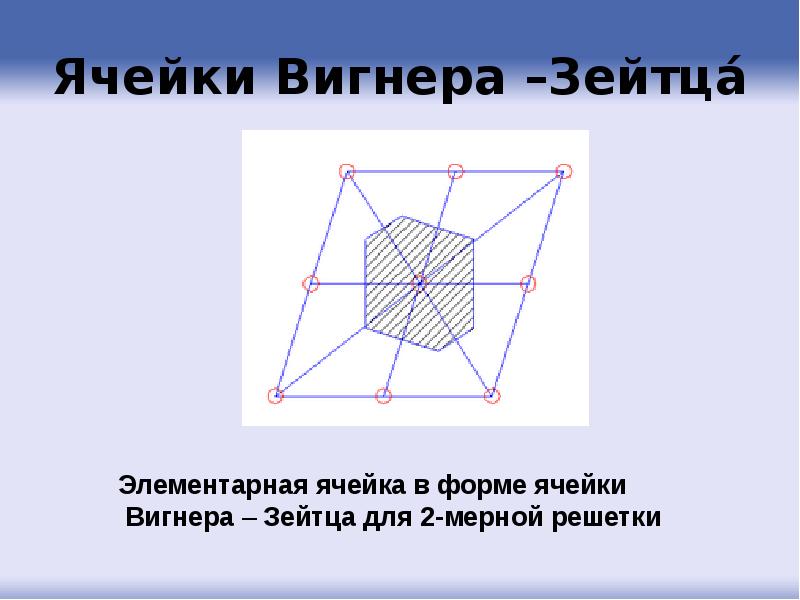
- 61. Ячейки Вигнера –Зейтца́
- 62. Ячейка Вингера –Зейтца это примитивная ячейка (содержит только один узел решетки), обладающая
- 63. Принцип построения зон Бриллюэна
- 64. Объем всех зон Бриллюэна одинаков и равен объему примитивной ячейки обратной
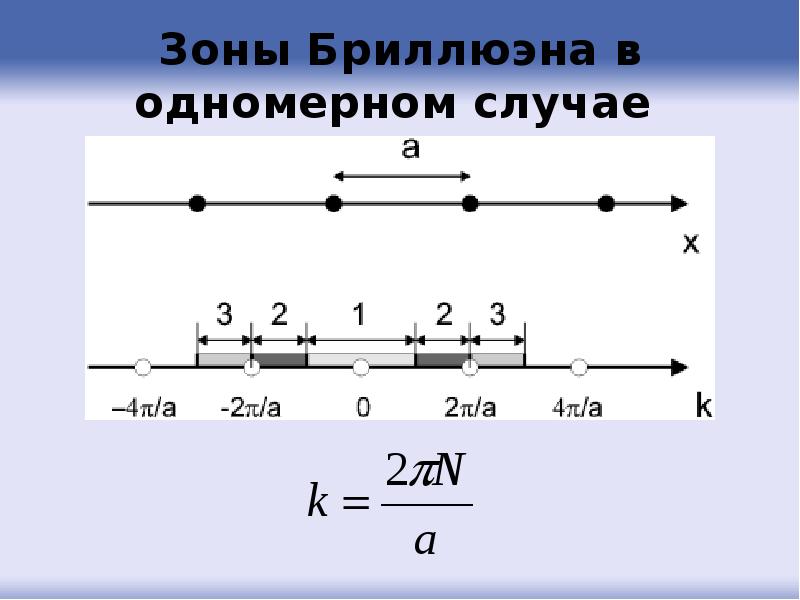
- 65. Зоны Бриллюэна в одномерном случае
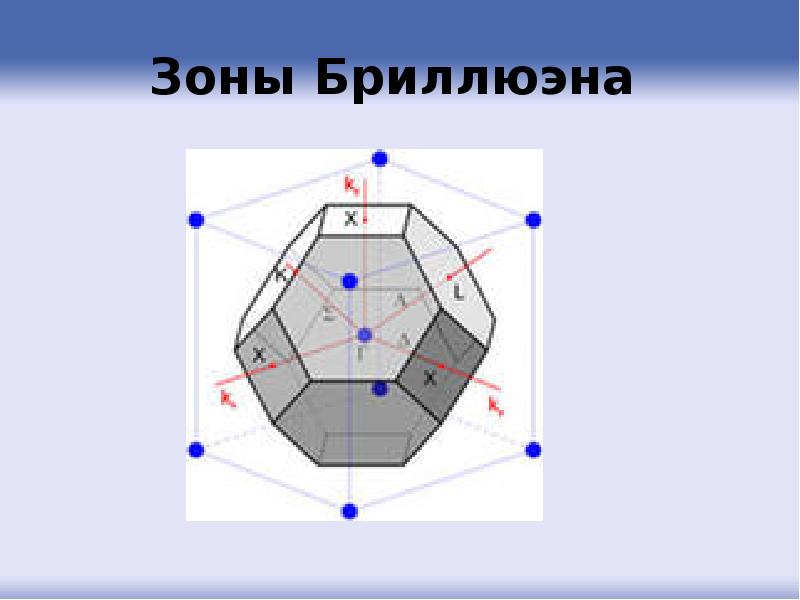
- 66. Зоны Бриллюэна
- 68. Для кристалла с простой кубической решеткой зона Бриллюэна в -пространстве
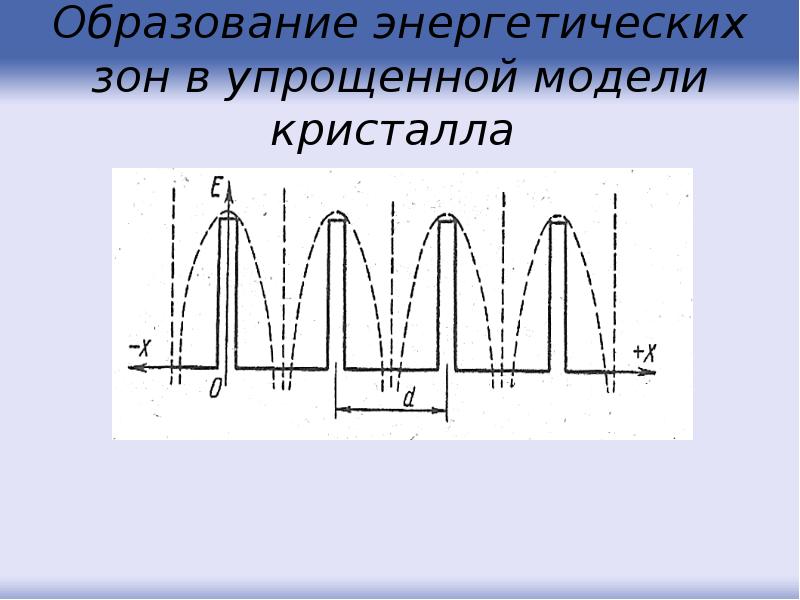
- 69. Образование энергетических зон в упрощенной модели кристалла
- 70. Если электрон заперт в атоме, кристалле или любой потенциальной яме, то
- 71. Предположив, что решение имеет вид Предположив, что решение имеет вид т.
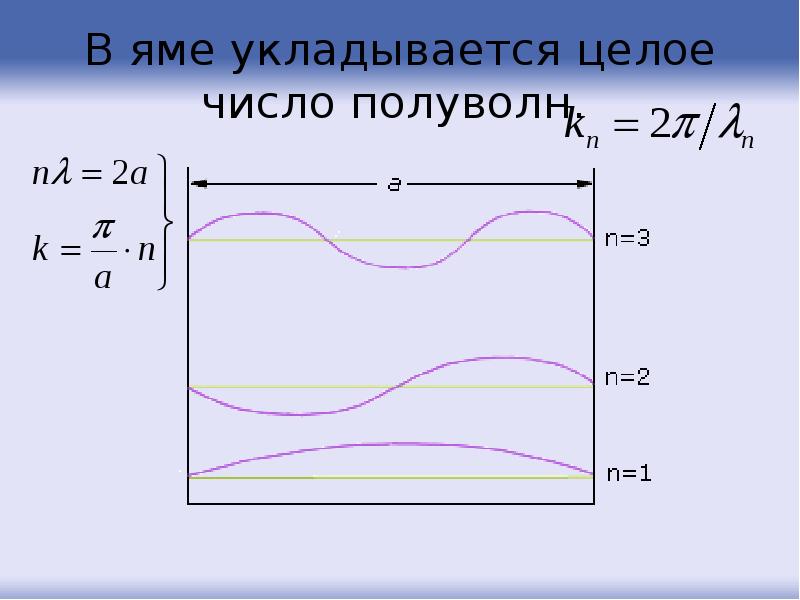
- 72. В яме укладывается целое число полуволн.
- 73. Волновую функцию такого электрона можно представит в следующем виде: Волновую функцию
- 74. Каждому уровню энергии Е1, Е2 ,… Еп соответствует своя стоячая электронная
- 75. Когда волновой вектор становится равным ,
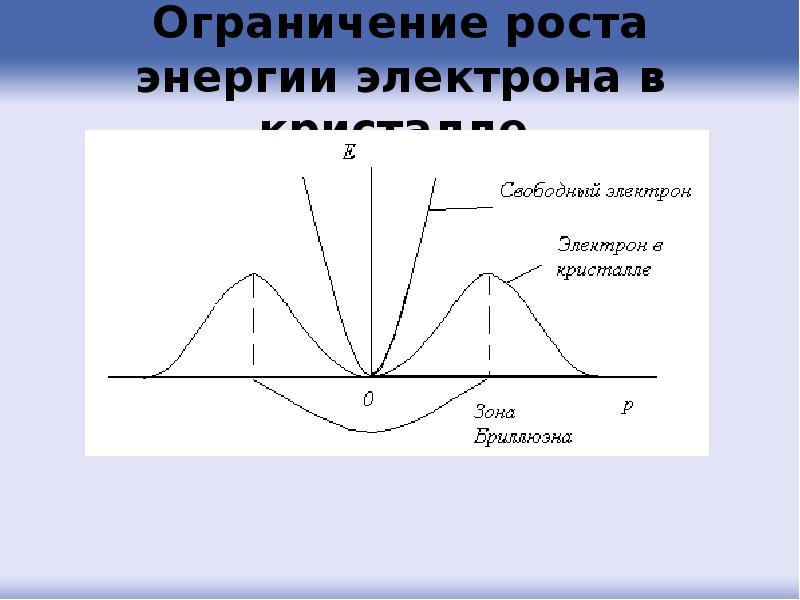
- 77. Ограничение роста энергии электрона в кристалле
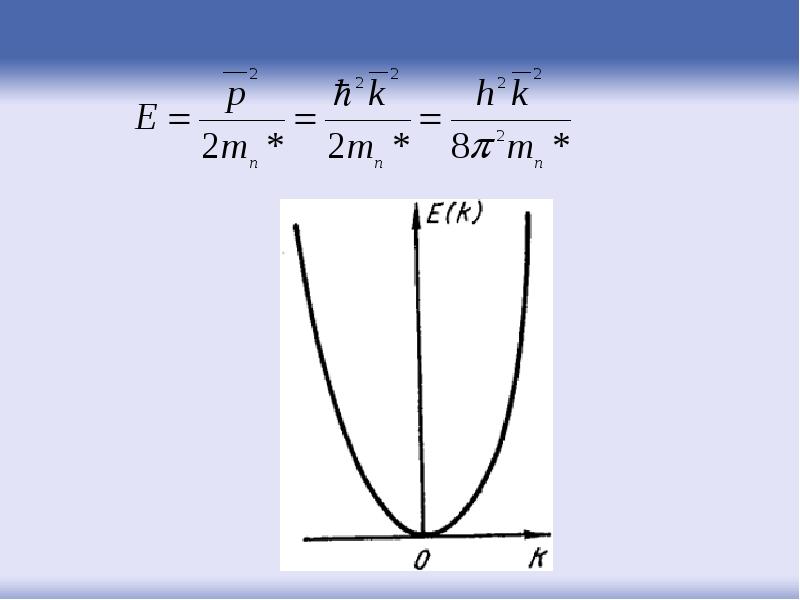
- 78. Вблизи нулевых значений импульса (волнового вектора) зависимость энергии очень мало отличается
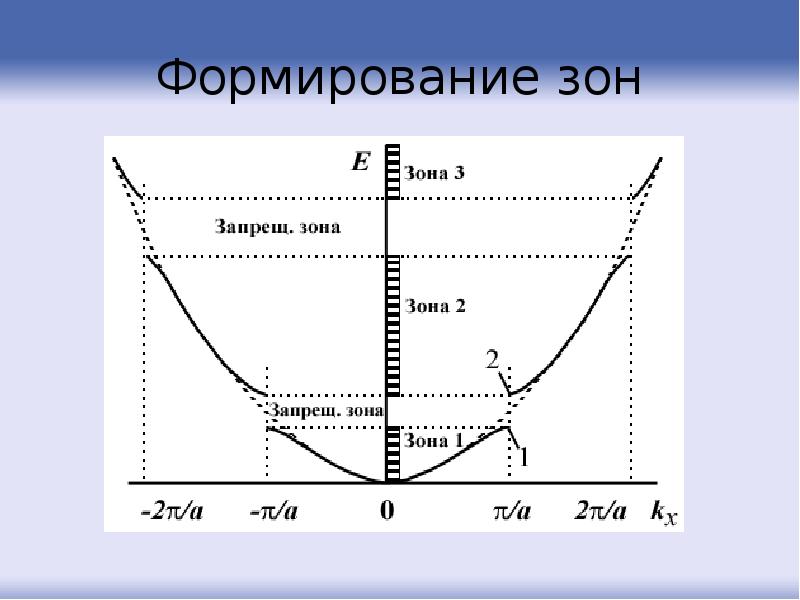
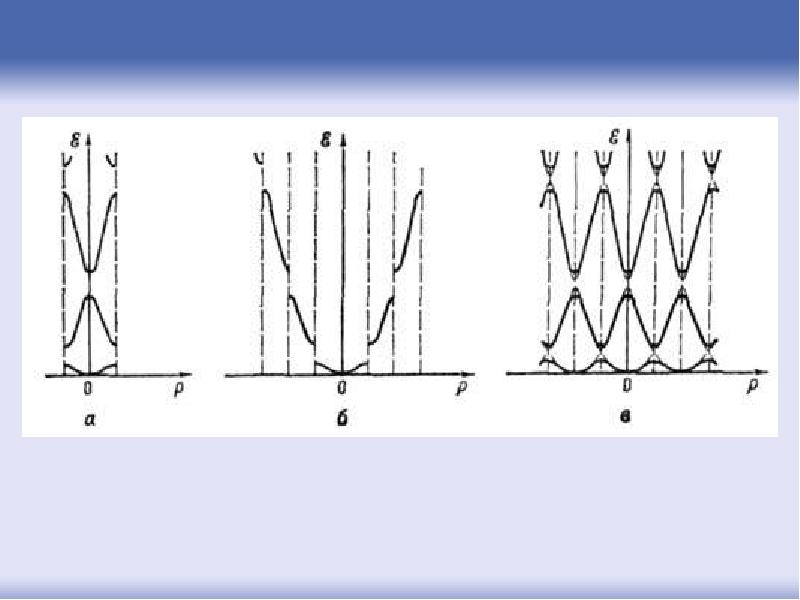
- 80. Формирование зон
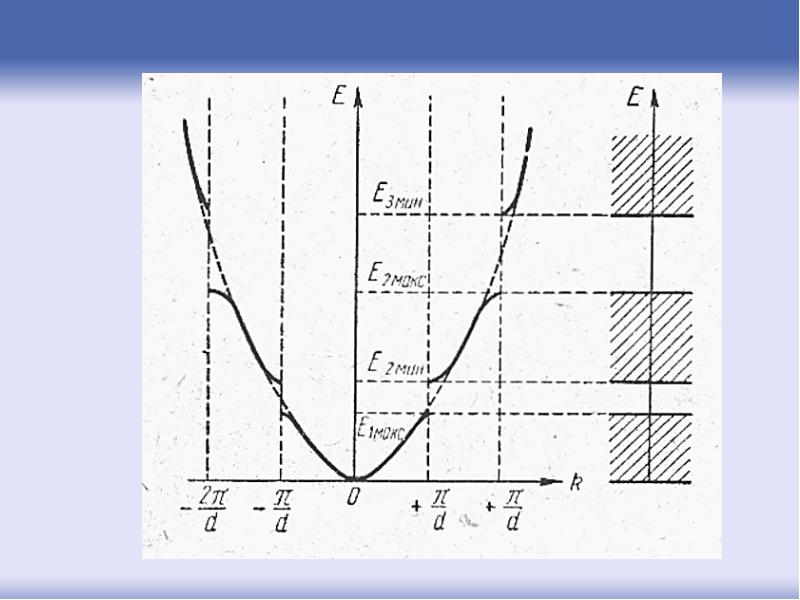
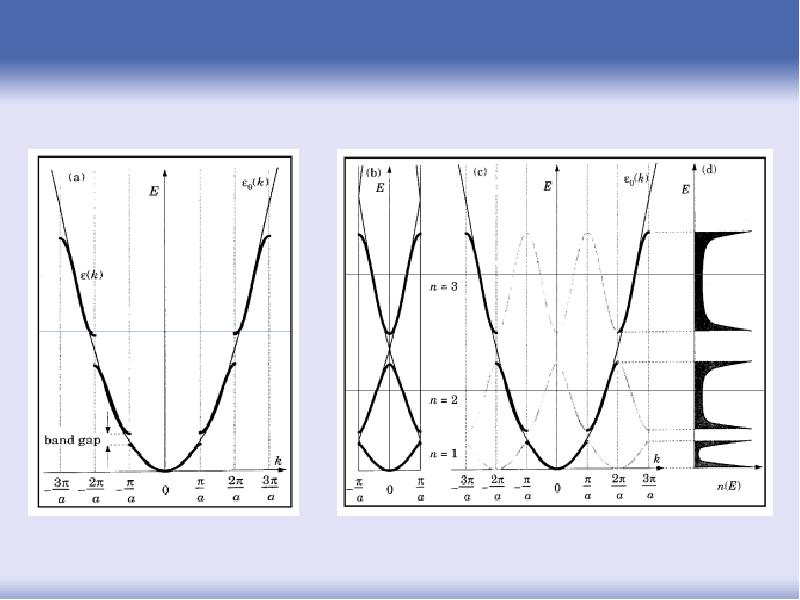
- 81. Соответственно разделению -пространства на зоны Бриллюэна, энергетический спектр электронов разделен
- 84. Таким образом, о зонах Бриллюэна говорим, когда имеем дело с
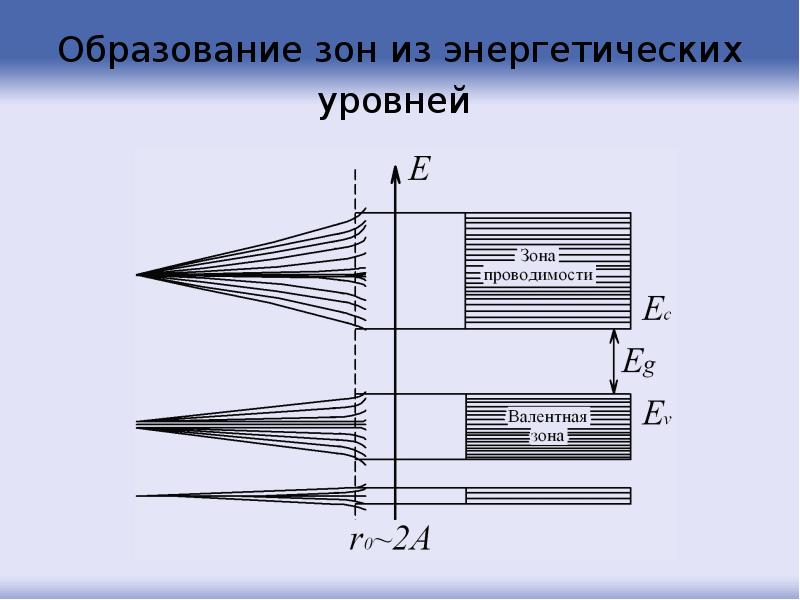
- 85. Образование зон из энергетических уровней
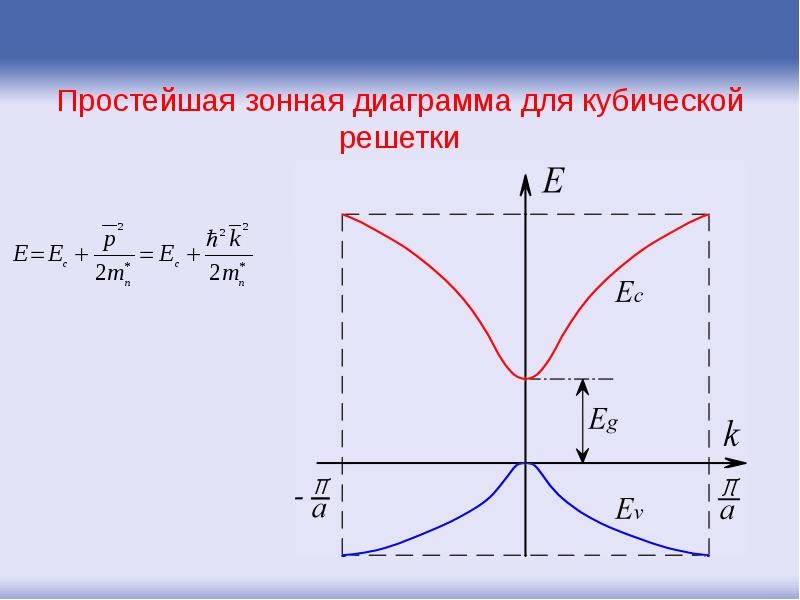
- 86. Простейшая зонная диаграмма для кубической решетки
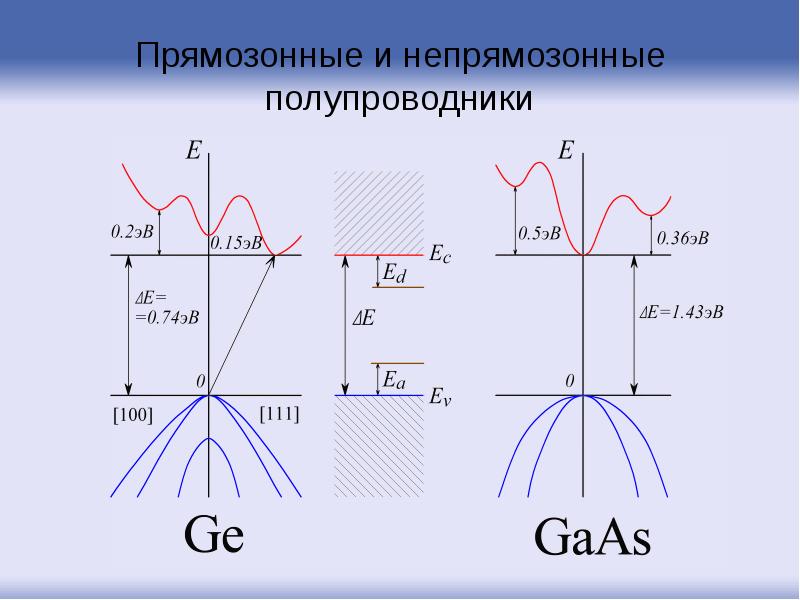
- 87. Прямозонные и непрямозонные полупроводники
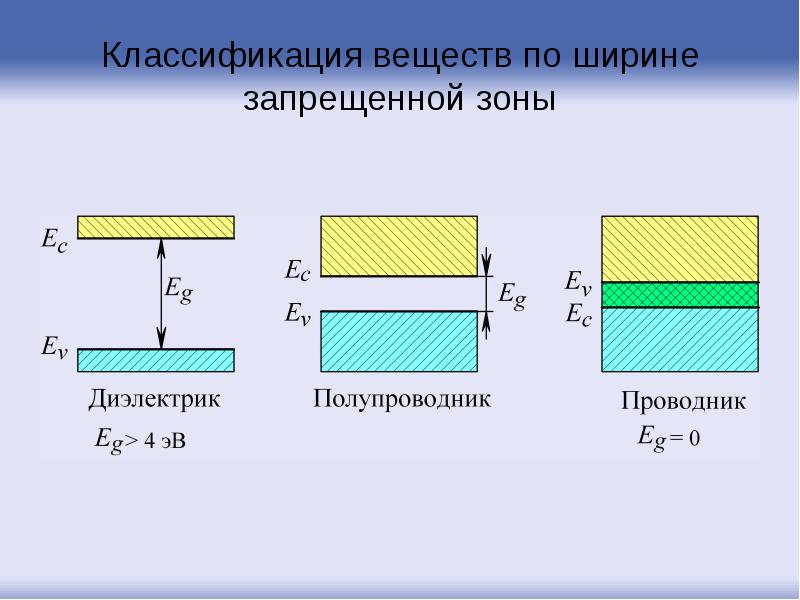
- 88. Классификация веществ по ширине запрещенной зоны
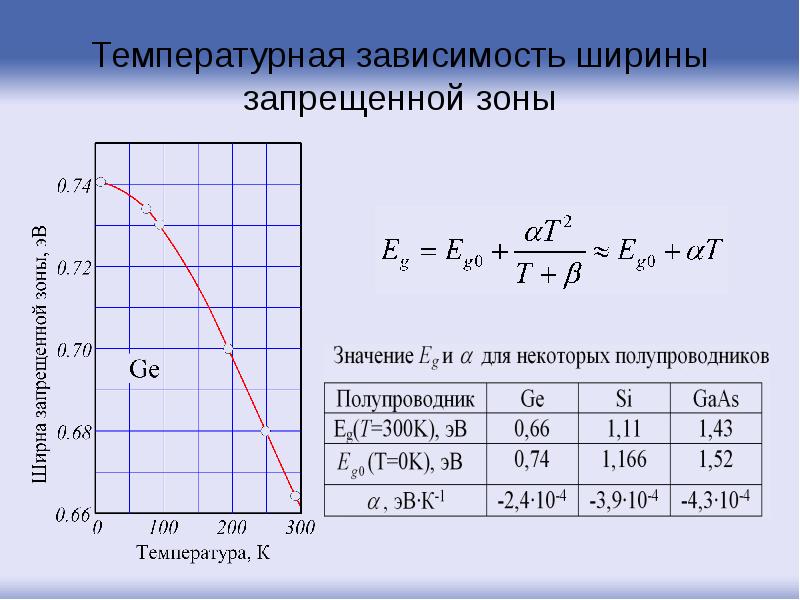
- 89. Температурная зависимость ширины запрещенной зоны
- 91. Зависимость энергии от квазиимпульса в InSb
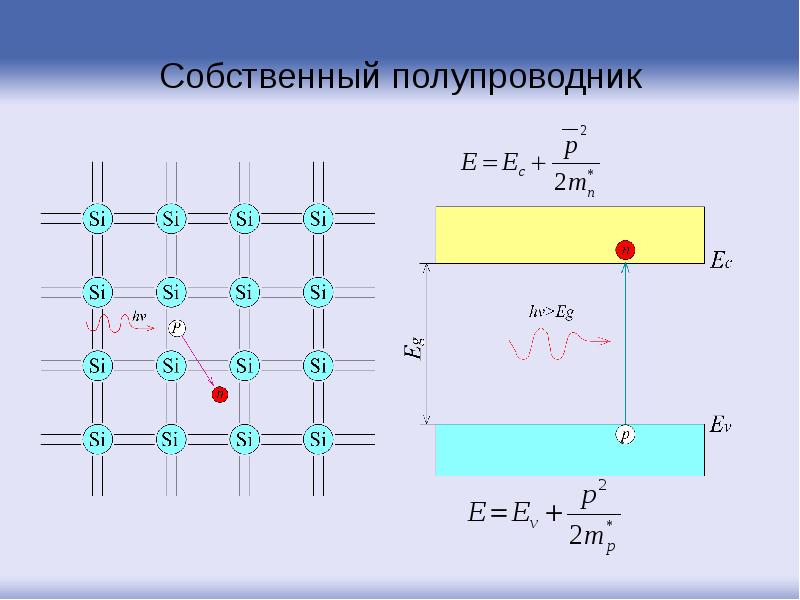
- 93. Собственный полупроводник
- 94. Собственный полупроводник
- 95. Собственный полупроводник Энергия, необходимая для увеличения концентрации носителей на единицу, называется
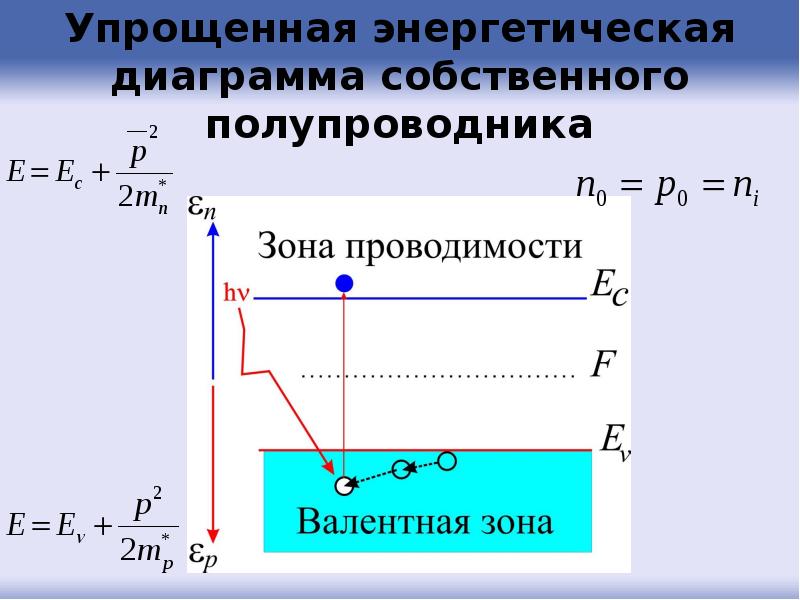
- 96. Упрощенная энергетическая диаграмма собственного полупроводника
- 97. Собственный полупроводник Концентрации носителей, находящихся в термодинамическом равновесии, равны между собой
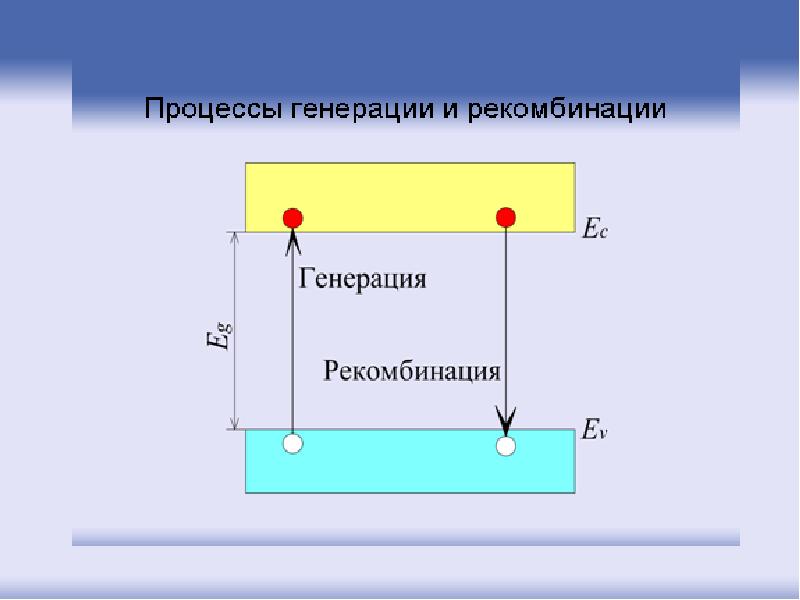
- 98. Собственный полупроводник Образовавшиеся в результате разрыва ковалентной связи (генерации) электрон и
- 99. Реальные кристаллы Реальные кристаллы несовершенны. Большинство кристаллов состоят из множества
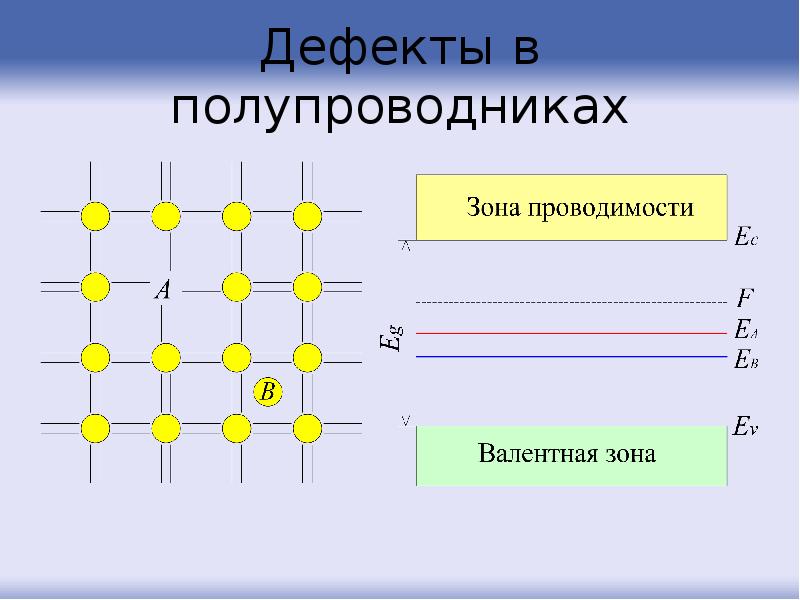
- 100. Дефекты в полупроводниках Наличие в кристалле дефектов приводит к появлению в
- 101. Дефекты в полупроводниках
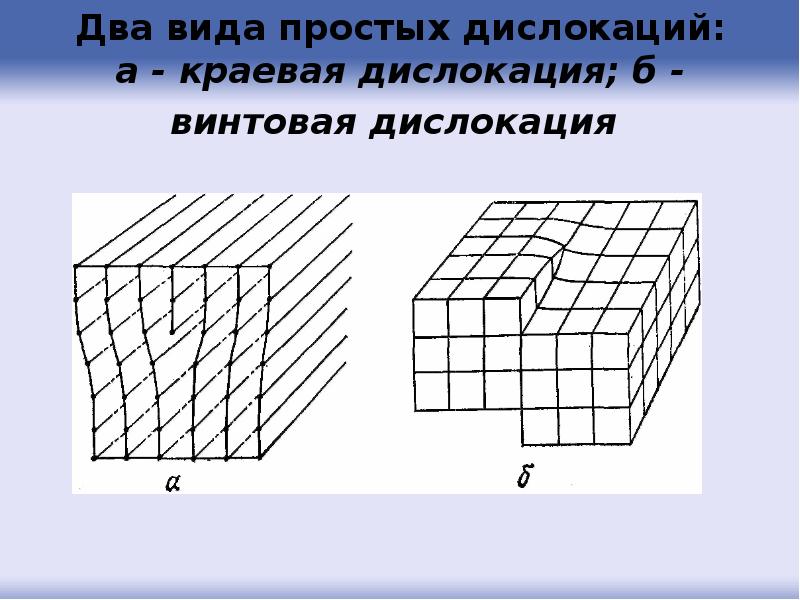
- 102. Два вида простых дислокаций: а - краевая дислокация; б - винтовая
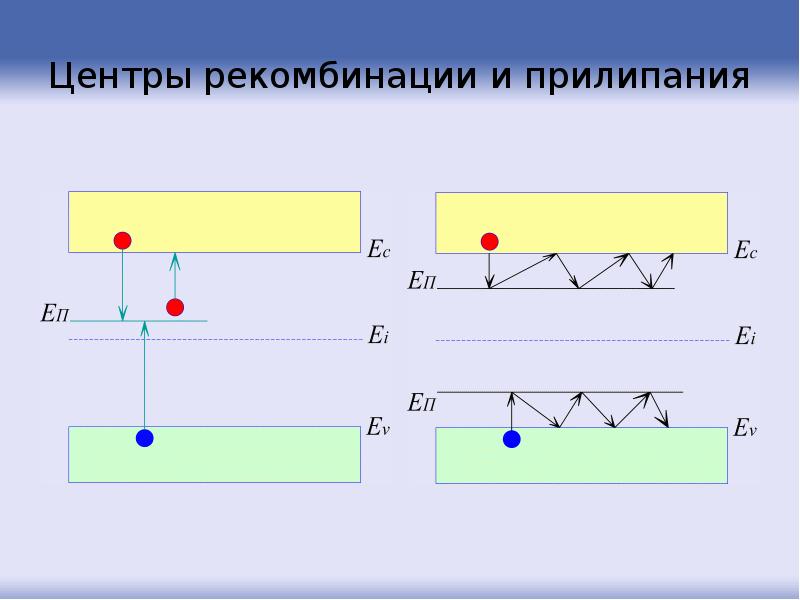
- 103. Центры рекомбинации и прилипания
- 104. Влияние поверхностных состояний на спектр энергетических уровней
- 105. Уравнение электронейтральности
- 106. Статистика электронов и дырок
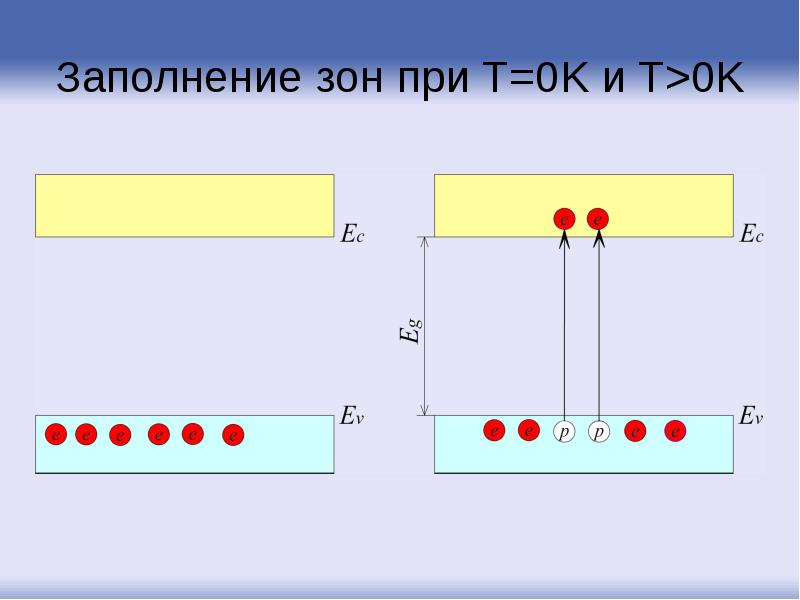
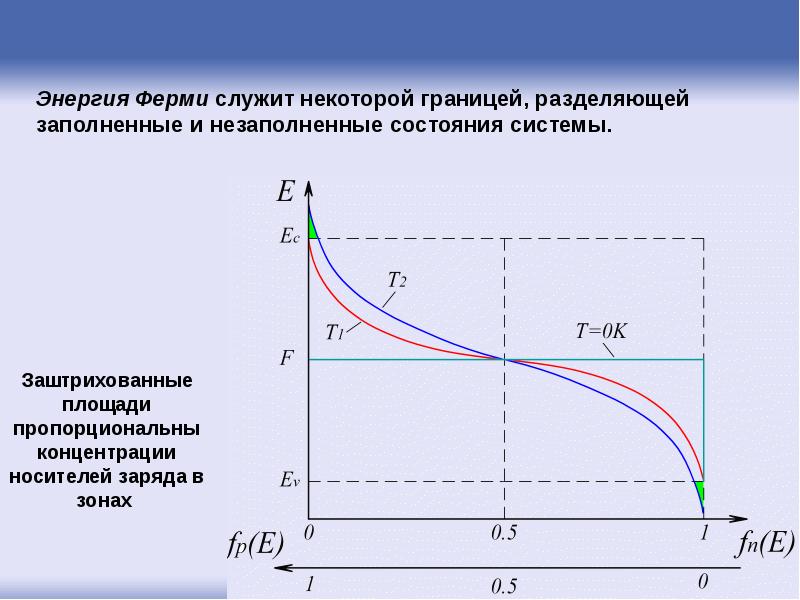
- 109. Заполнение зон при T=0K и T>0K
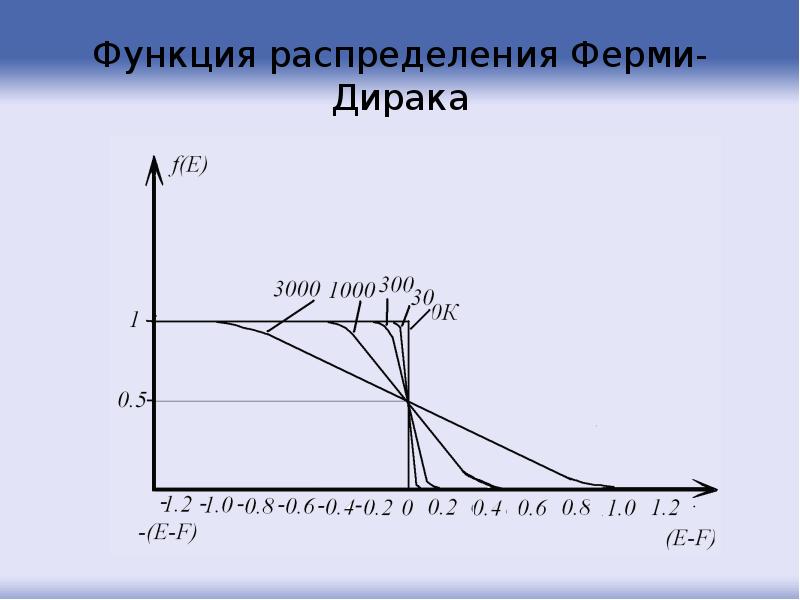
- 111. Функция распределения Ферми-Дирака
- 115. Статистика Максвелла-Больцмана и Ферми-Дирака
- 116. Больцман (Boltzmann) Людвиг Австрийский физик, один из основоположников статистической физики и
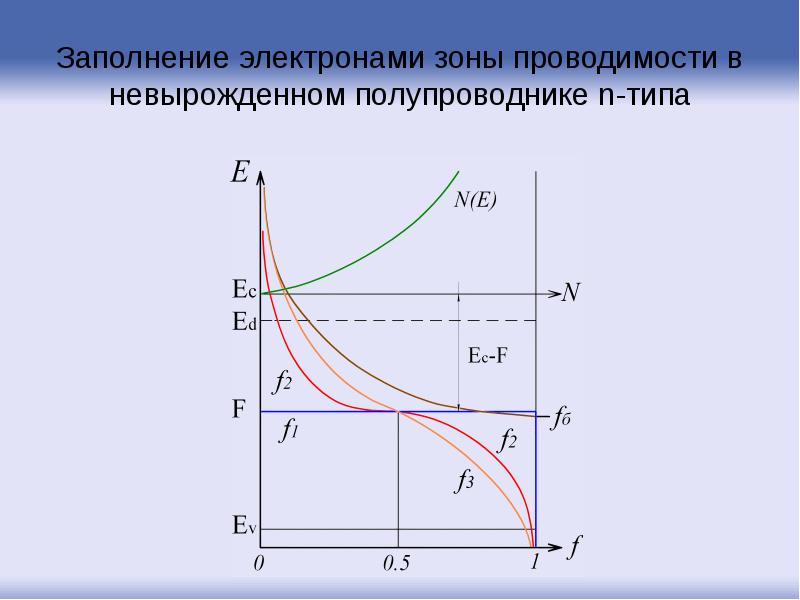
- 117. Заполнение электронами зоны проводимости в невырожденном полупроводнике n-типа
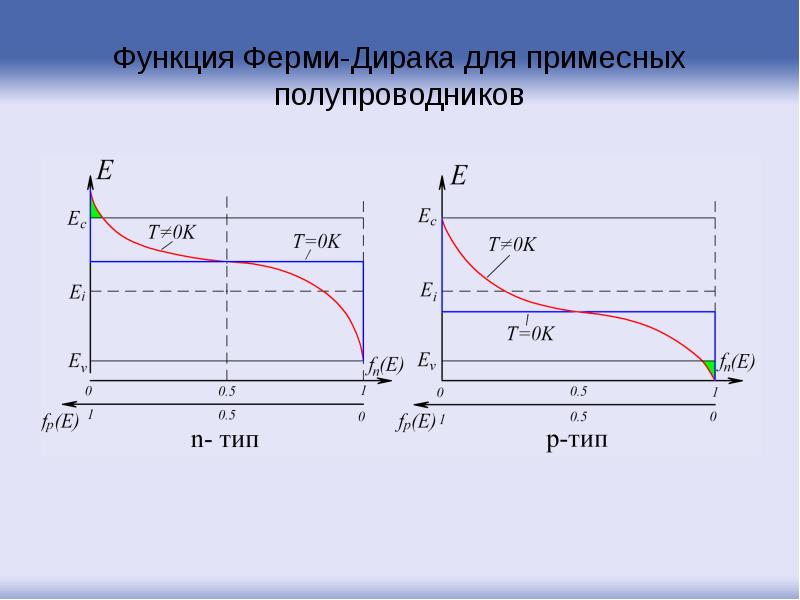
- 118. Функция Ферми-Дирака для примесных полупроводников
- 121. Заполнение электронами и дырками зон невырожденного полупроводника
- 124. Эффективная плотность состояний
- 125. Уравнение электронейтральности
- 126. Расчет положения уровня Ферми для собственного полупроводника
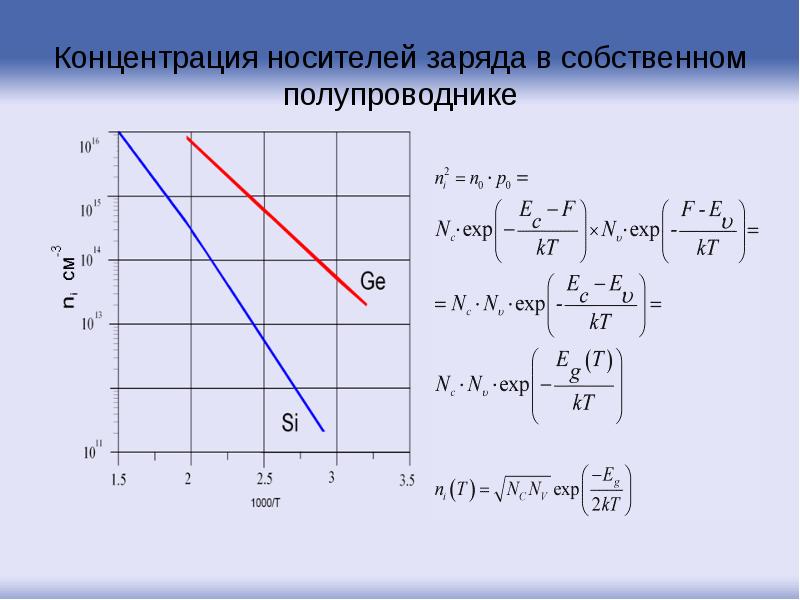
- 127. Концентрация носителей заряда в собственном полупроводнике
- 128. Типичные значения собственной концентрации для некоторых полупроводников
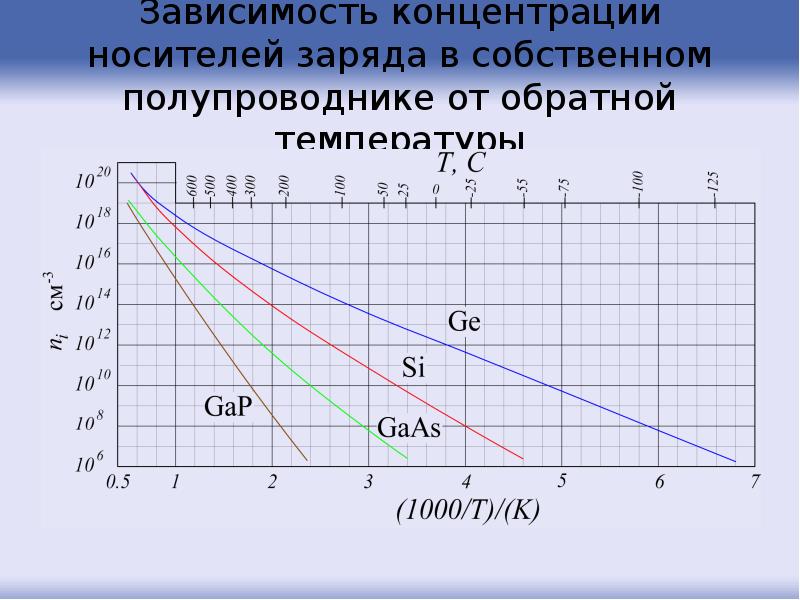
- 129. Зависимость концентрации носителей заряда в собственном полупроводнике от обратной температуры
- 130. Скачать презентацию






















































































Слайды и текст этой презентации
Скачать презентацию на тему Основы зонной теории твердого тела можно ниже:
Похожие презентации