Переходные процессы в цепях первого порядка презентация
Содержание
- 2. Переходные процессы В линейной электрической цепи, содержащей реактивные элементы, при переходе
- 3. Законы коммутации Первый закон: в ветви электрической цепи с катушками индуктивности
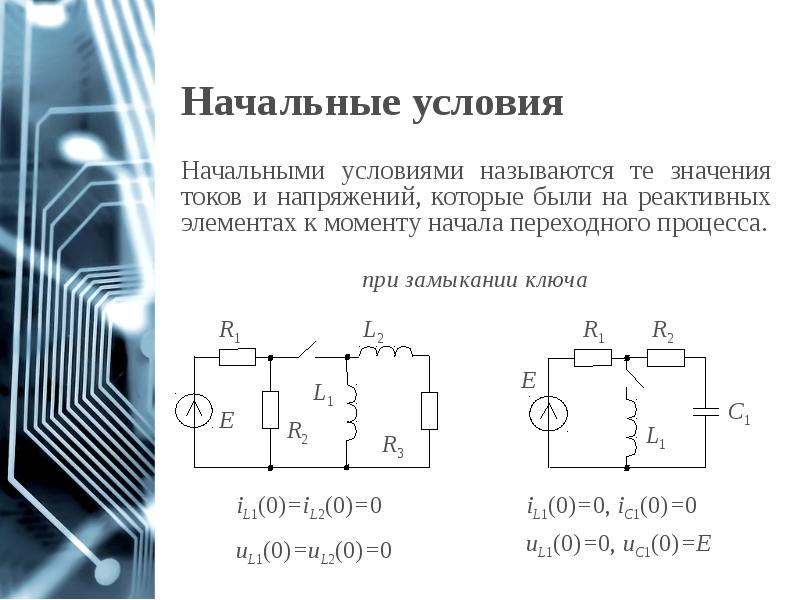
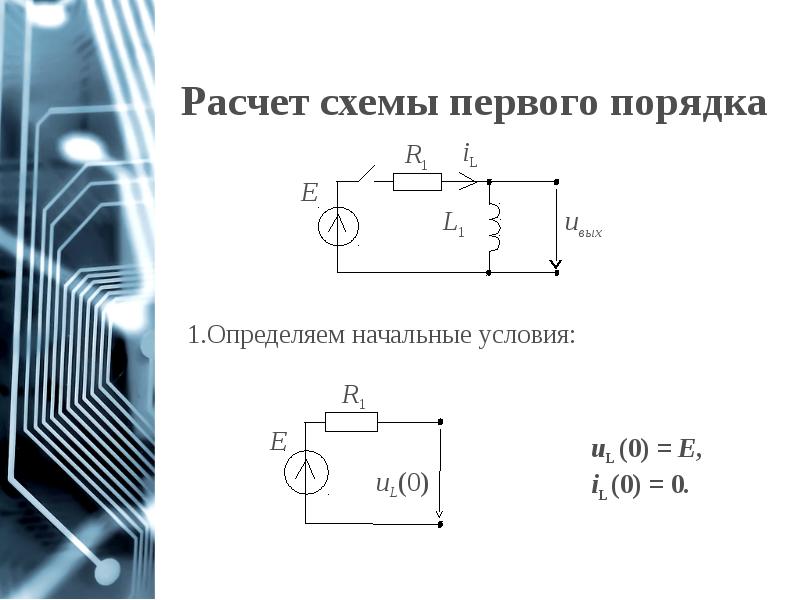
- 4. Начальные условия Начальными условиями называются те значения токов и напряжений, которые
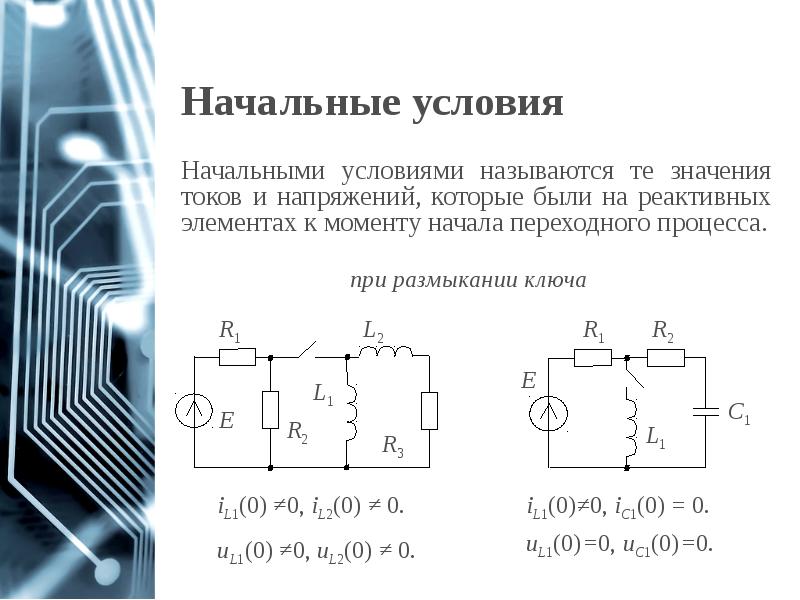
- 5. Начальные условия Начальными условиями называются те значения токов и напряжений, которые
- 6. Математическое описание Дифференциальное уравнение, описывающее переходный процесс в цепи с n
- 7. Решение диф. уравнения Решение дифференциального уравнения в общем случае имеет вид:
- 8. Классический метод расчета Алгоритм расчета переходных процессов классическим методом: 1)
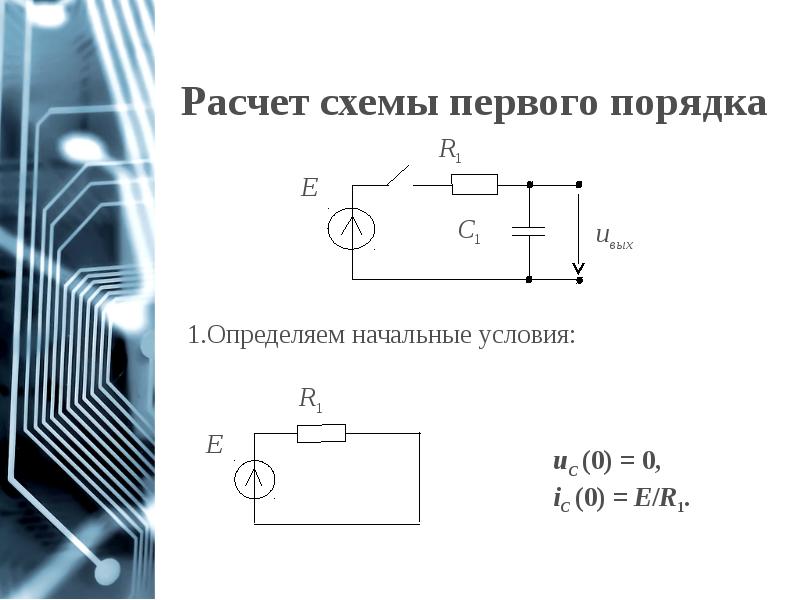
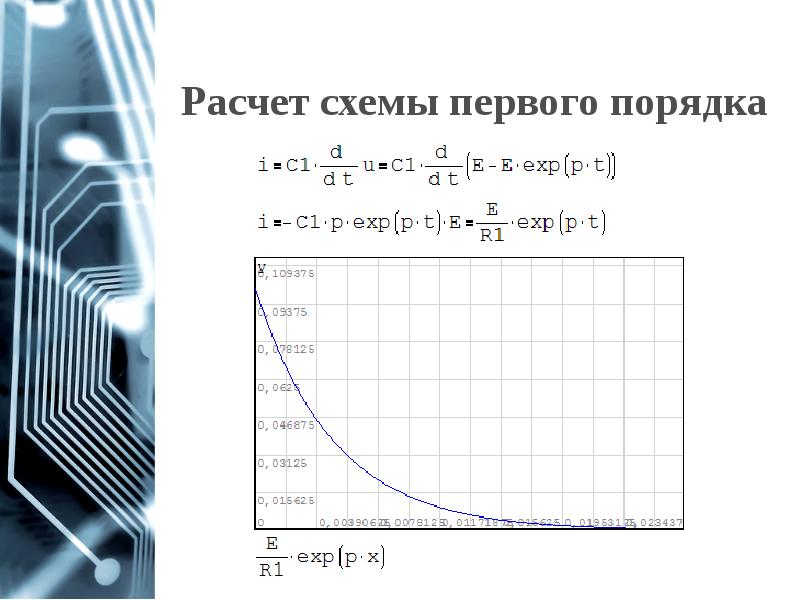
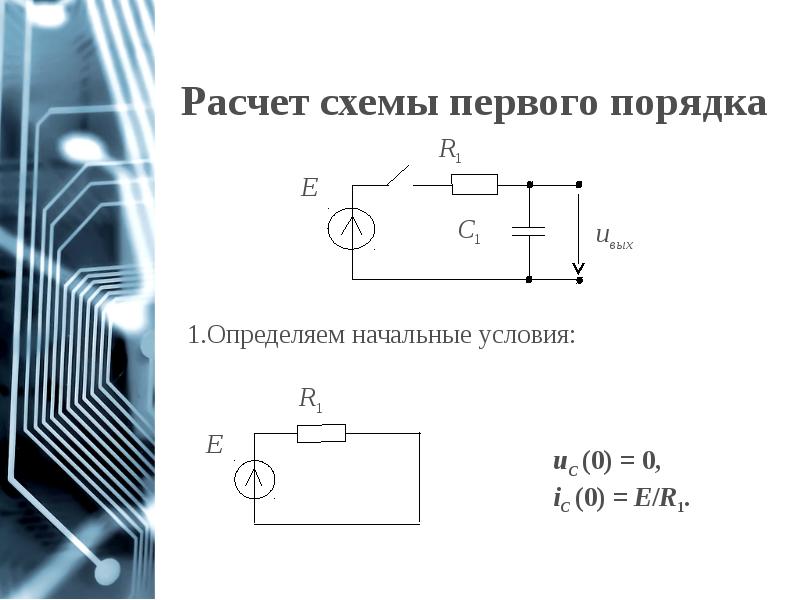
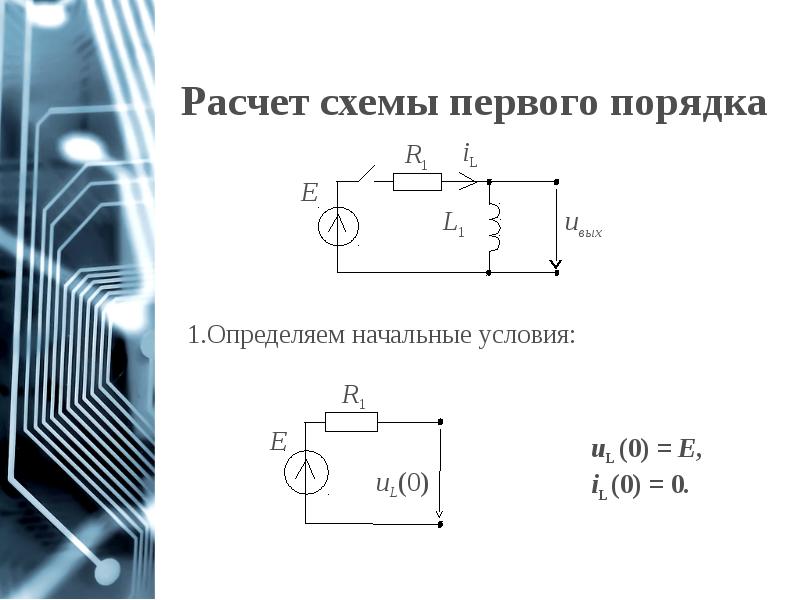
- 9. Расчет схемы первого порядка
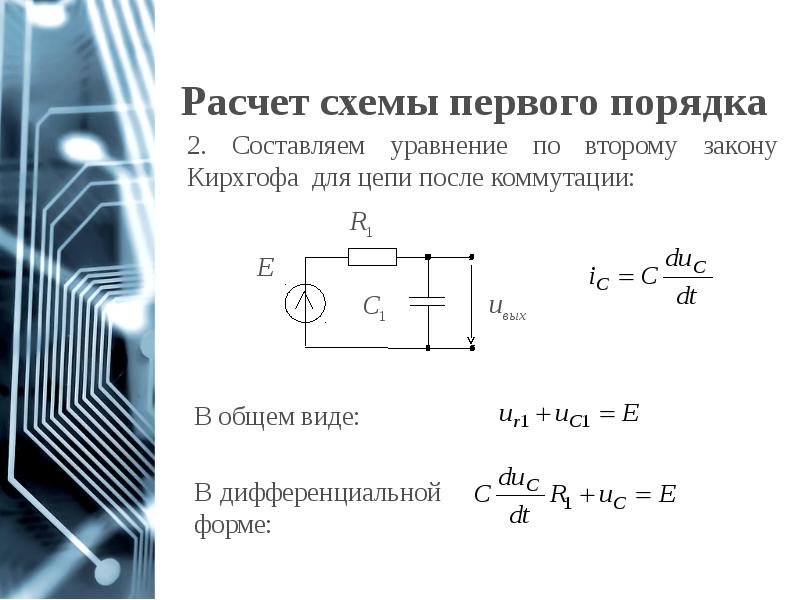
- 10. Расчет схемы первого порядка
- 11. Расчет схемы первого порядка
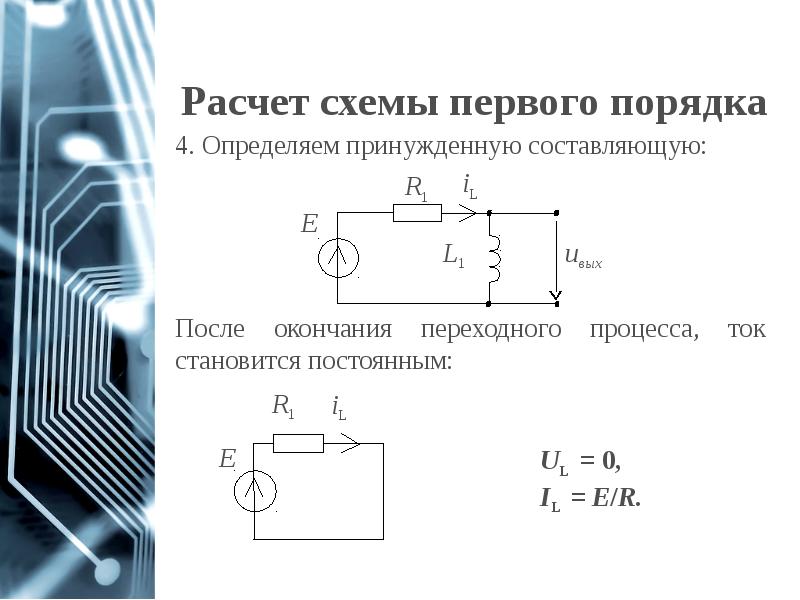
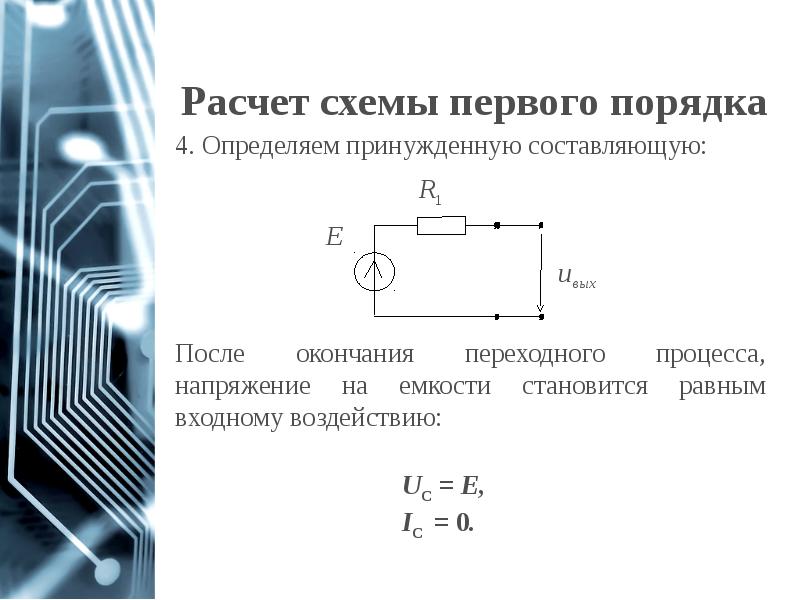
- 12. Расчет схемы первого порядка
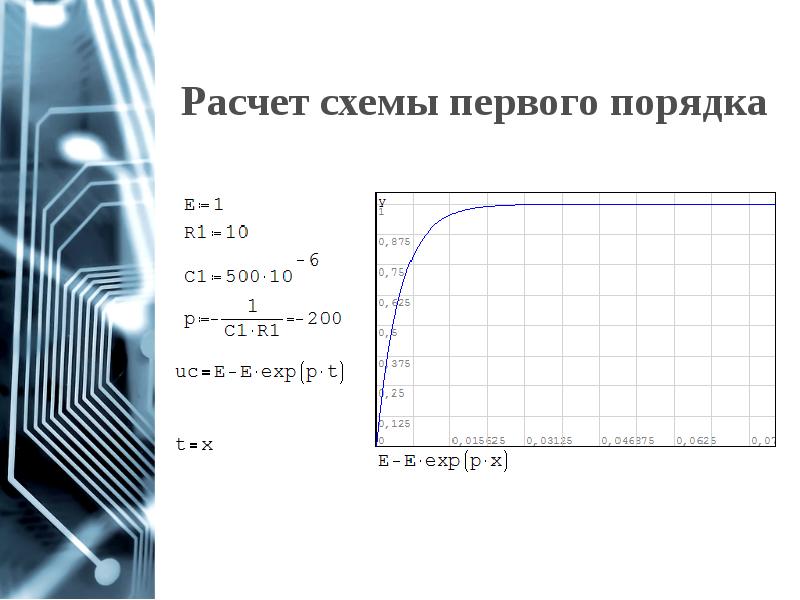
- 13. Расчет схемы первого порядка
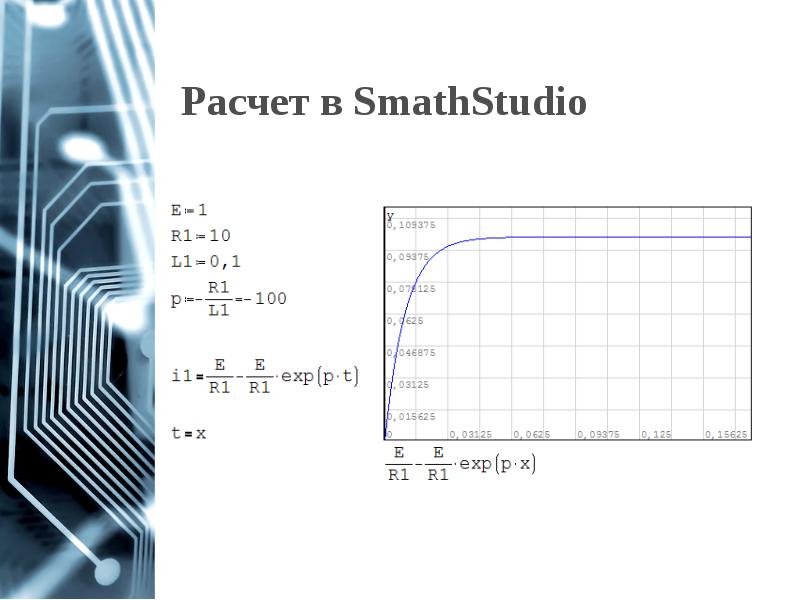
- 14. Расчет в SmathStudio
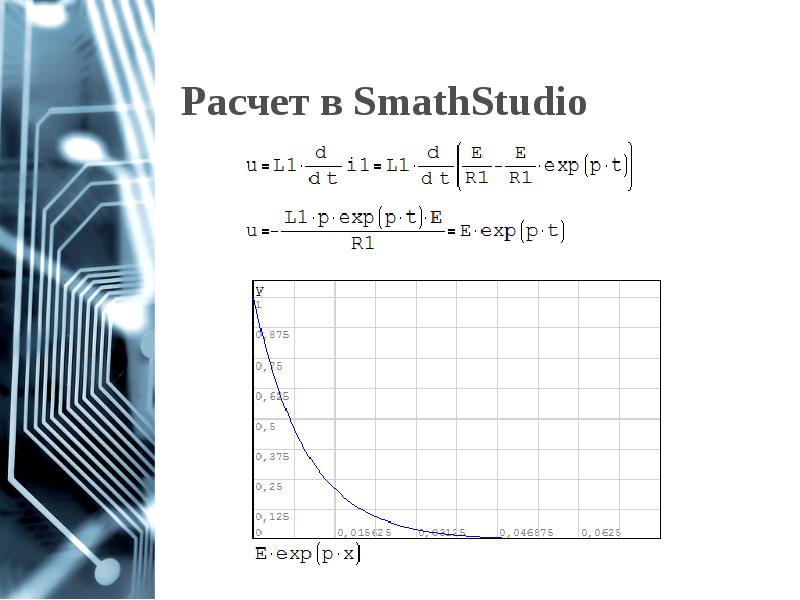
- 15. Расчет в SmathStudio
- 16. Расчет схемы первого порядка
- 17. Расчет схемы первого порядка
- 18. Расчет схемы первого порядка
- 19. Расчет схемы первого порядка
- 20. Расчет схемы первого порядка
- 21. Расчет схемы первого порядка
- 22. Расчет схемы первого порядка
- 23. Расчет схемы первого порядка
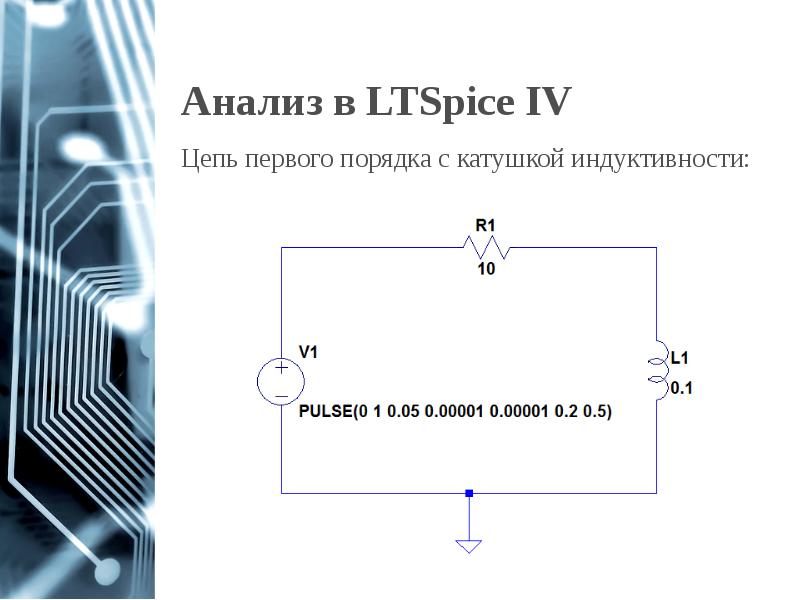
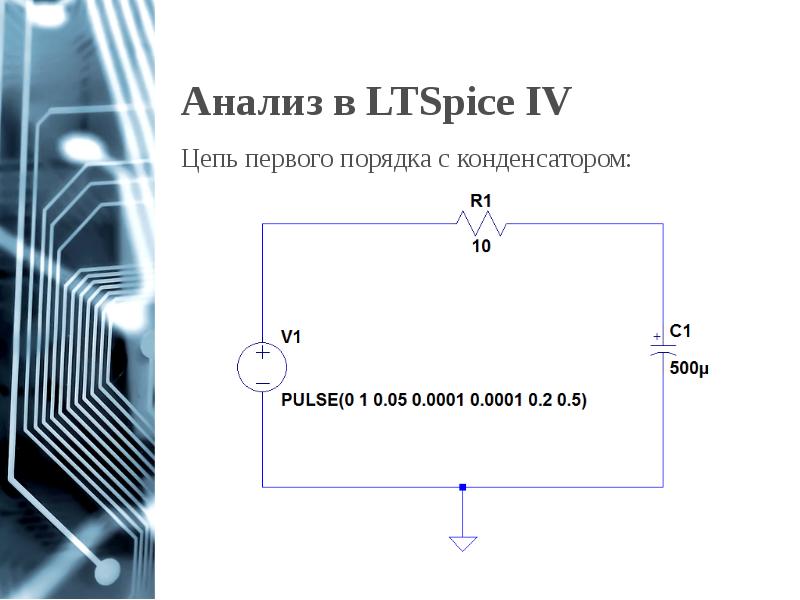
- 24. Анализ в LTSpice IV
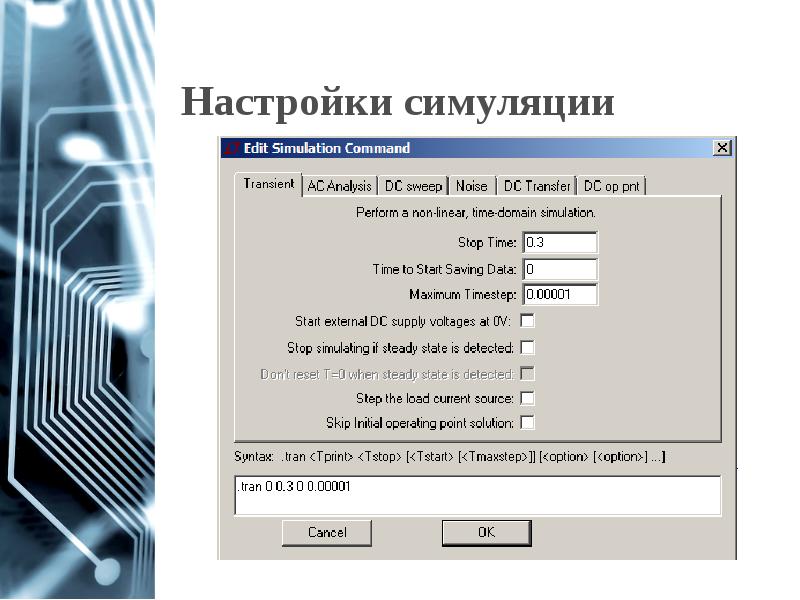
- 25. Настройки симуляции
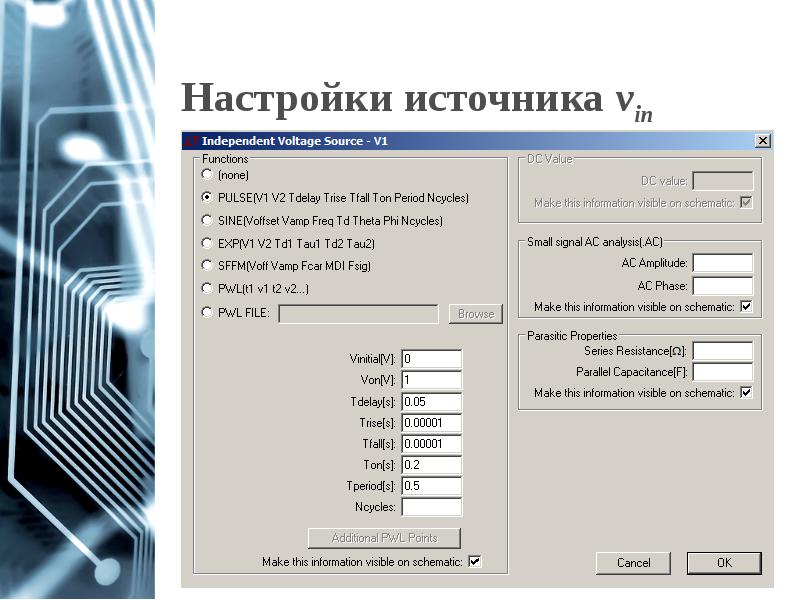
- 26. Настройки источника vin
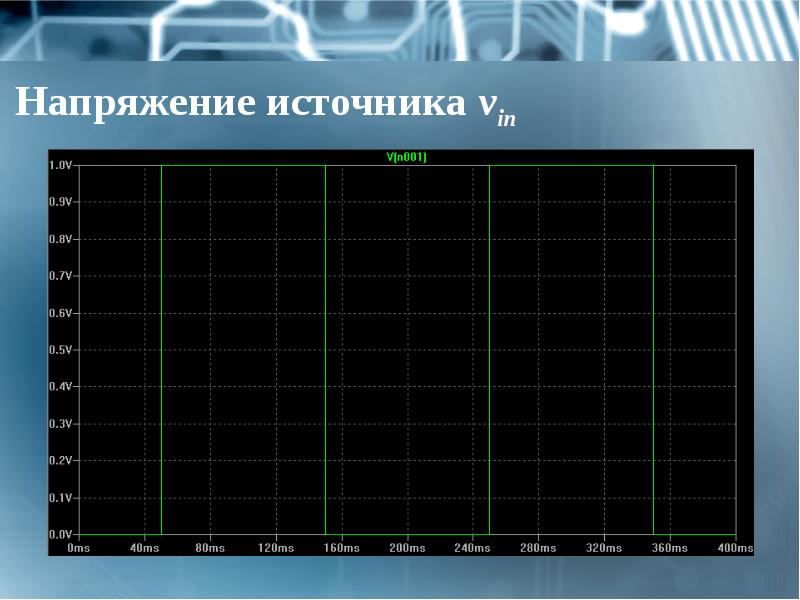
- 27. Напряжение источника vin
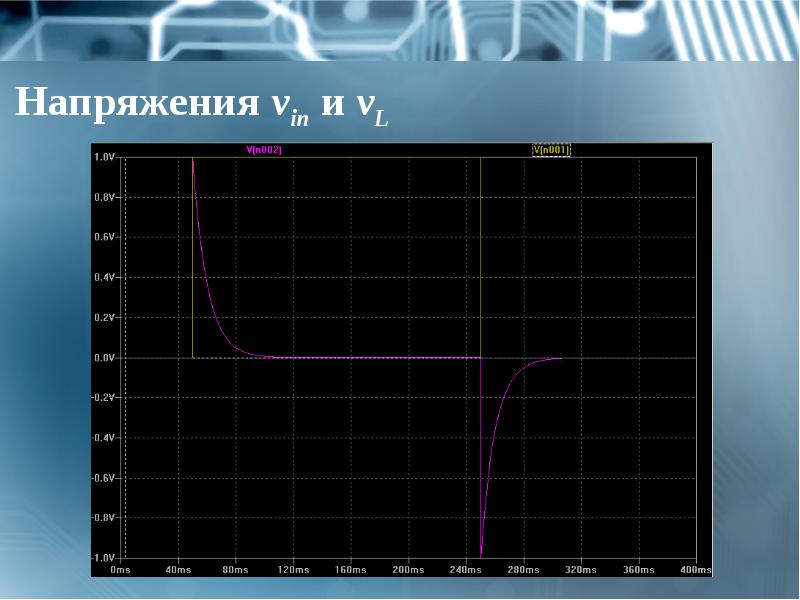
- 28. Напряжения vin и vL
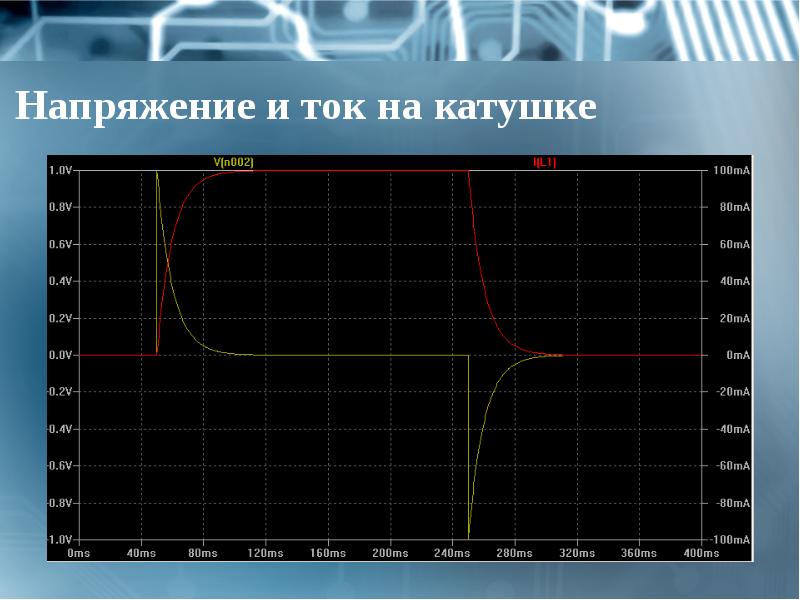
- 29. Напряжение и ток на катушке
- 30. Анализ в LTSpice IV
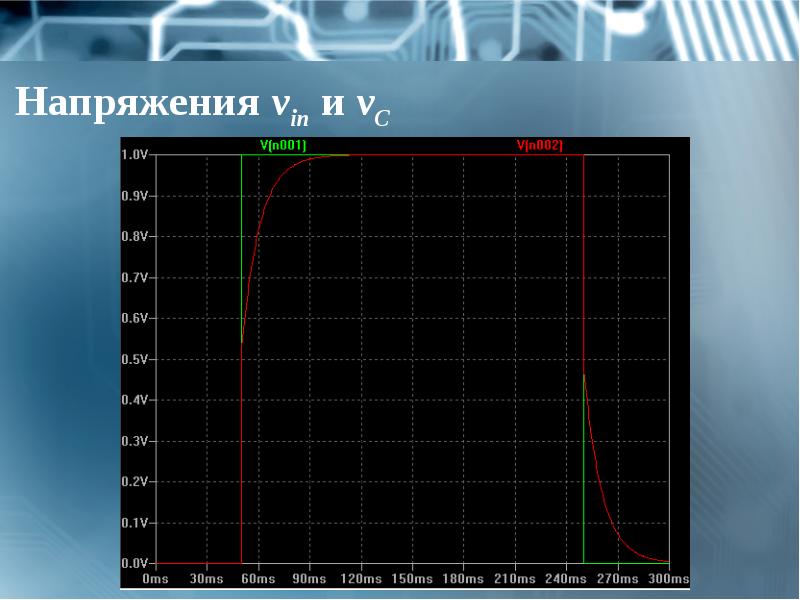
- 31. Напряжения vin и vС
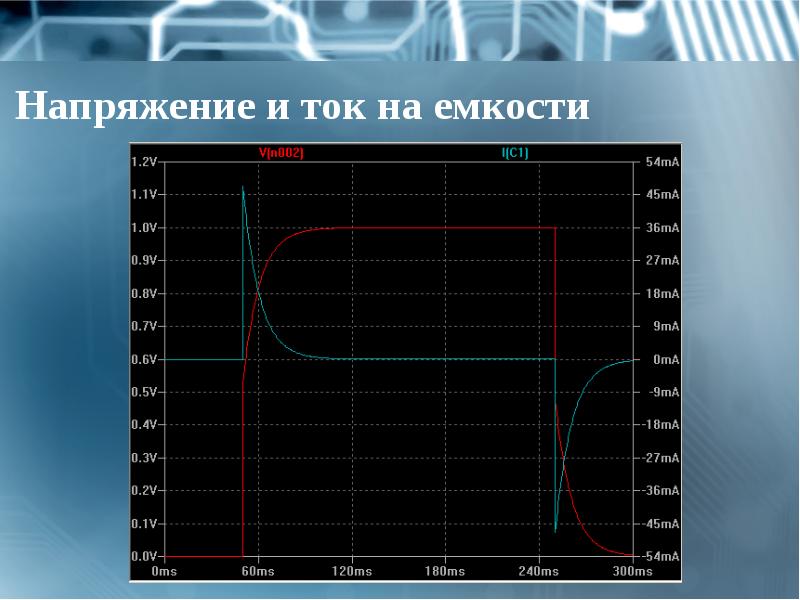
- 32. Напряжение и ток на емкости
- 33. Операторный метод Хевисайда Дифференциальное уравнение может быть представлено операторным изображением. Сложные
- 34. Преобразование Лапласа
- 35. Оригиналы и их изображения
- 36. Оригиналы и их изображения
- 37. Формула разложения
- 38. Формула разложения
- 39. Формула разложения
- 40. Операторный метод расчета Алгоритм расчета переходных процессов операторным методом: 1)
- 41. Операторные изображения
- 42. Операторные изображения
- 43. Операторные изображения
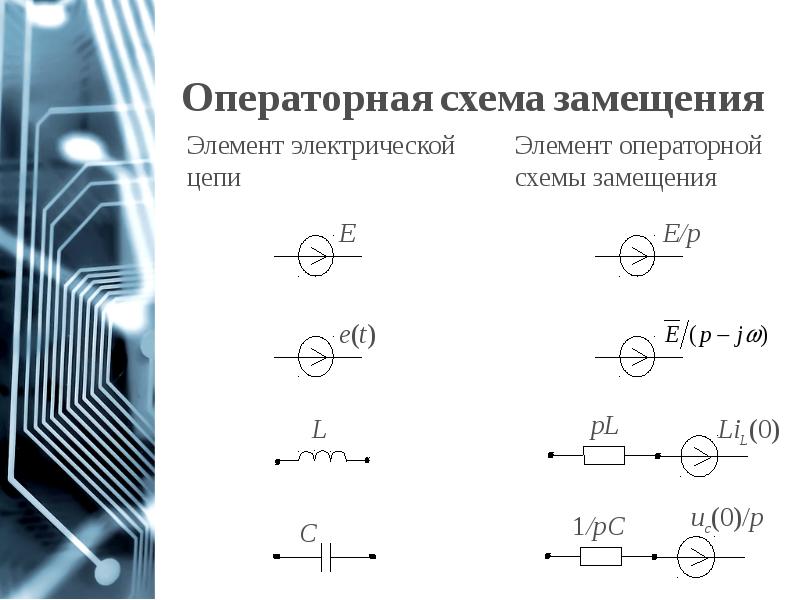
- 44. Операторная схема замещения
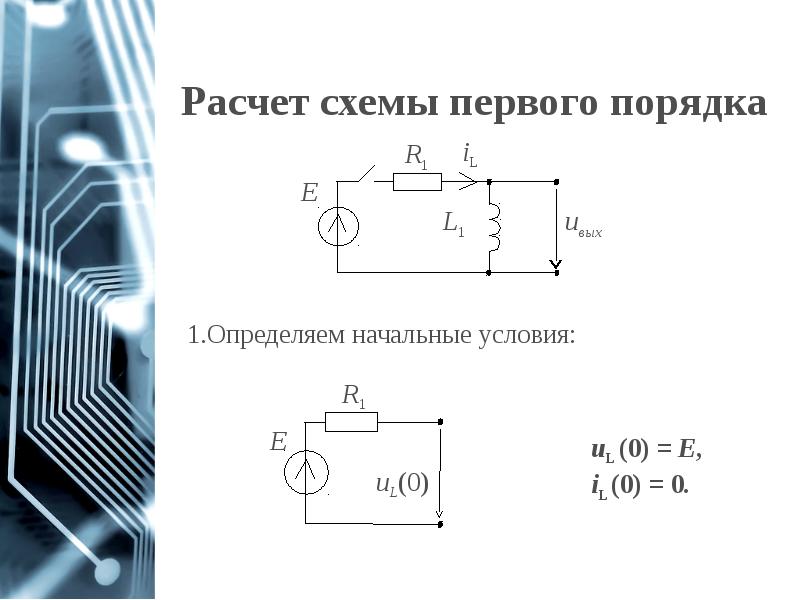
- 45. Расчет схемы первого порядка
- 46. Расчет схемы первого порядка
- 47. Расчет схемы первого порядка
- 48. Расчет схемы первого порядка
- 49. Расчет схемы первого порядка
- 50. Расчет схемы первого порядка
- 51. Расчет схемы первого порядка
- 52. Расчет схемы первого порядка
- 53. Расчет схемы первого порядка
- 54. Расчет схемы первого порядка
- 55. Переходной процесс в цепи переменного тока Алгоритм расчета переходных процессов в
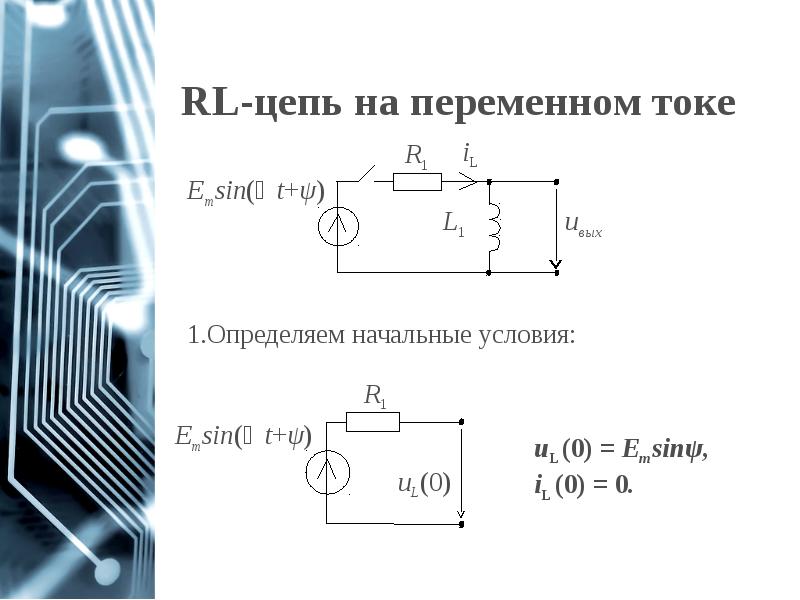
- 56. RL-цепь на переменном токе
- 57. RL-цепь на переменном токе
- 58. RL-цепь на переменном токе
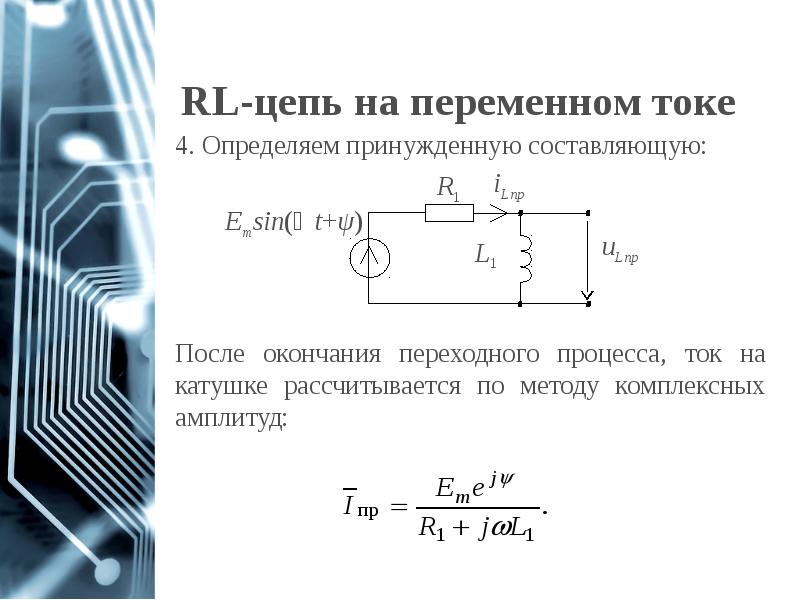
- 59. RL-цепь на переменном токе
- 60. RL-цепь на переменном токе
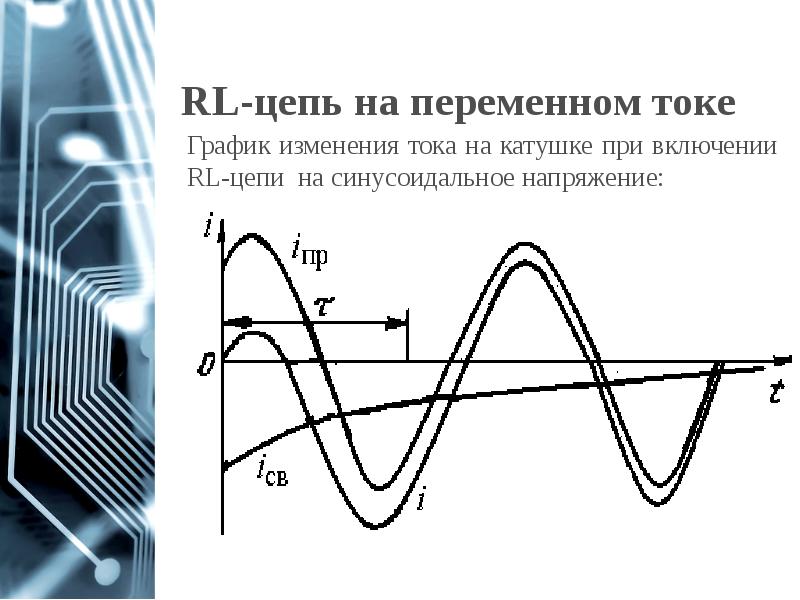
- 61. RL-цепь на переменном токе
- 62. RL-цепь на переменном токе
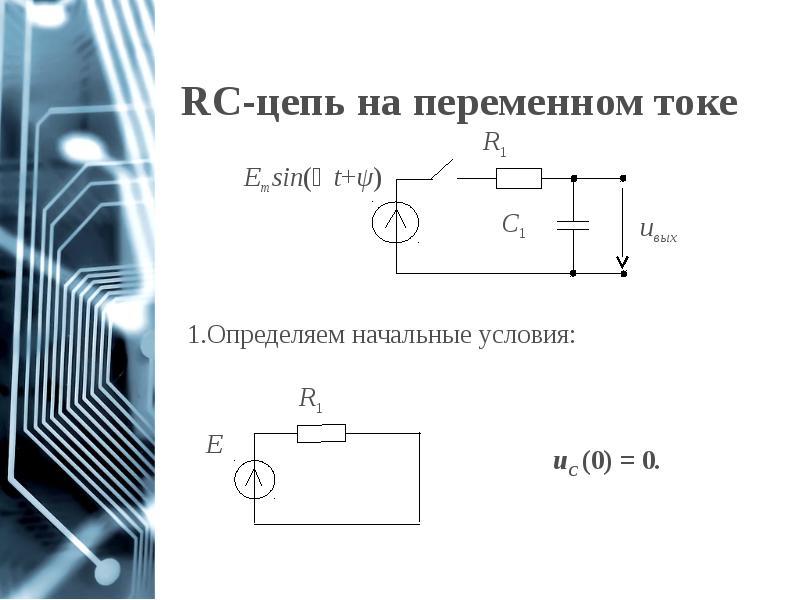
- 63. RC-цепь на переменном токе
- 64. RC-цепь на переменном токе
- 65. RC-цепь на переменном токе
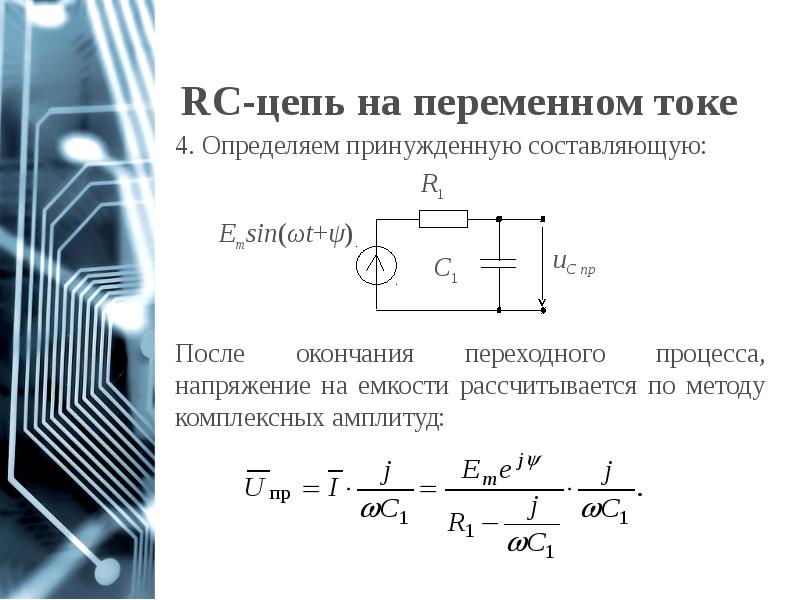
- 66. RC-цепь на переменном токе
- 67. RC-цепь на переменном токе
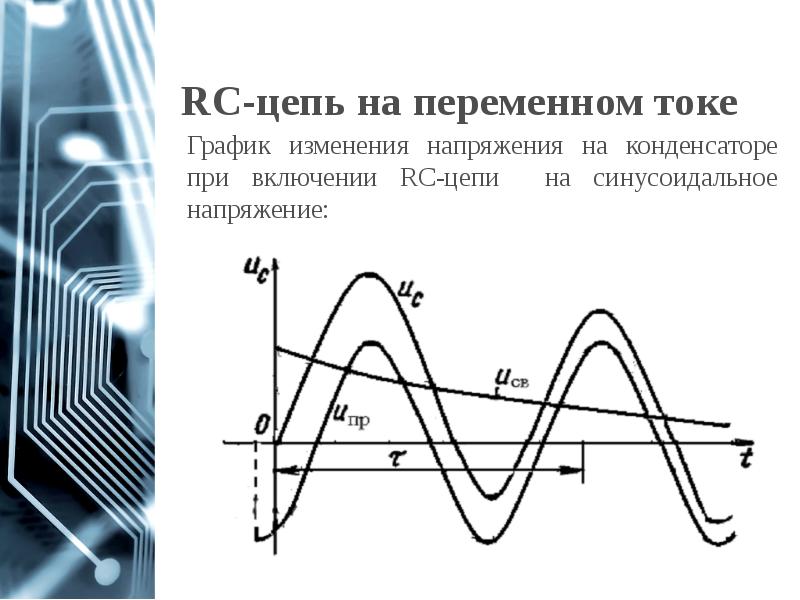
- 68. RC-цепь на переменном токе
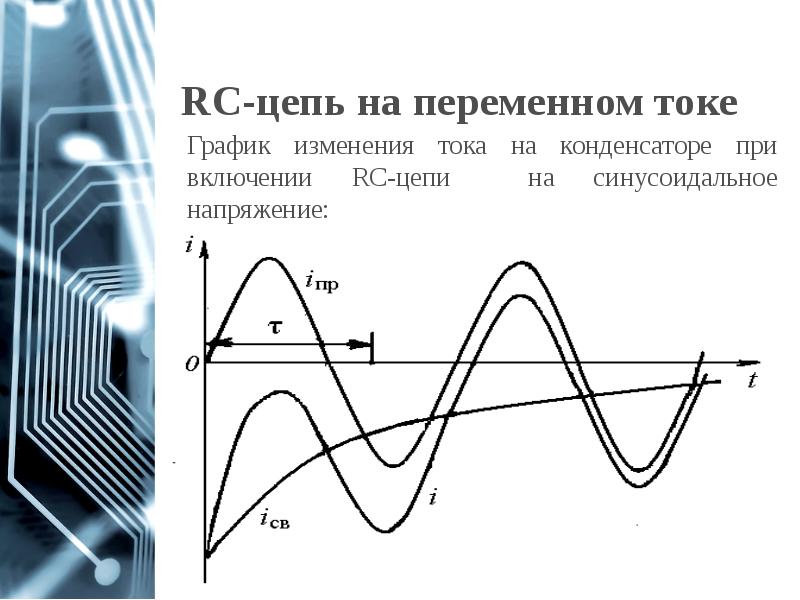
- 69. RC-цепь на переменном токе
- 70. RC-цепь на переменном токе
- 71. Расчет схемы первого порядка
- 72. Расчет схемы первого порядка
- 73. Расчет схемы первого порядка
- 74. Расчет схемы первого порядка
- 75. Скачать презентацию











































Слайды и текст этой презентации
Скачать презентацию на тему Переходные процессы в цепях первого порядка можно ниже:
Похожие презентации