Применение первого начала термодинамики к изопроцессам презентация
Содержание
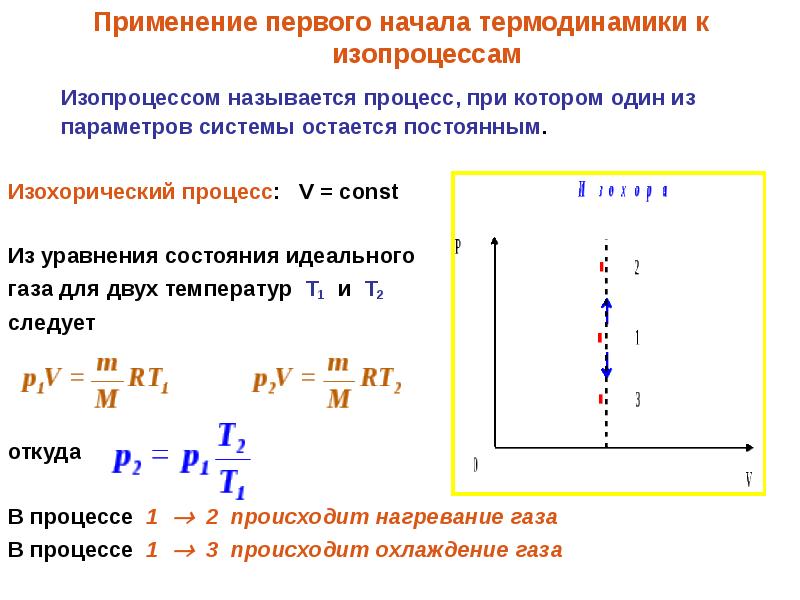
- 2. Пусть начальное состояние газа отвечает состоянию при нормальных условиях Т0 =
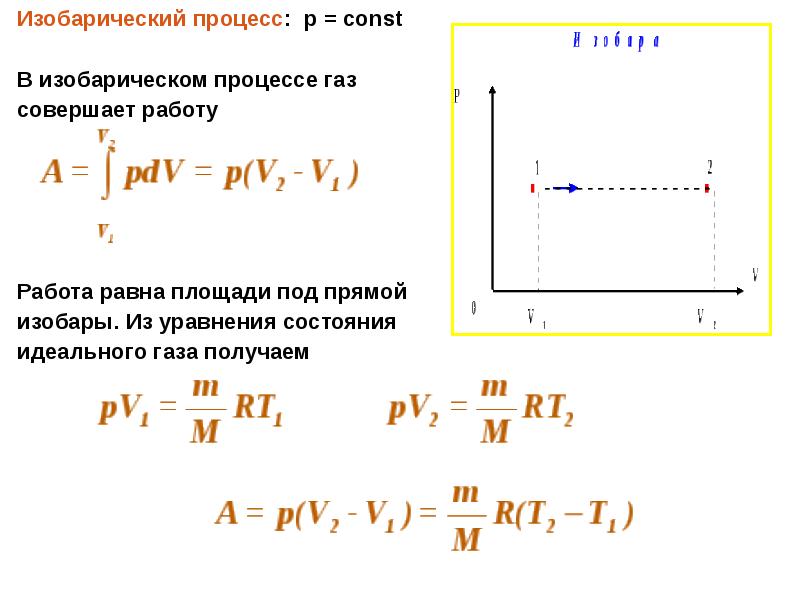
- 3. Изобарический процесс: p = const Изобарический процесс: p = const
- 4. Перепишем последнее соотношение в виде Это
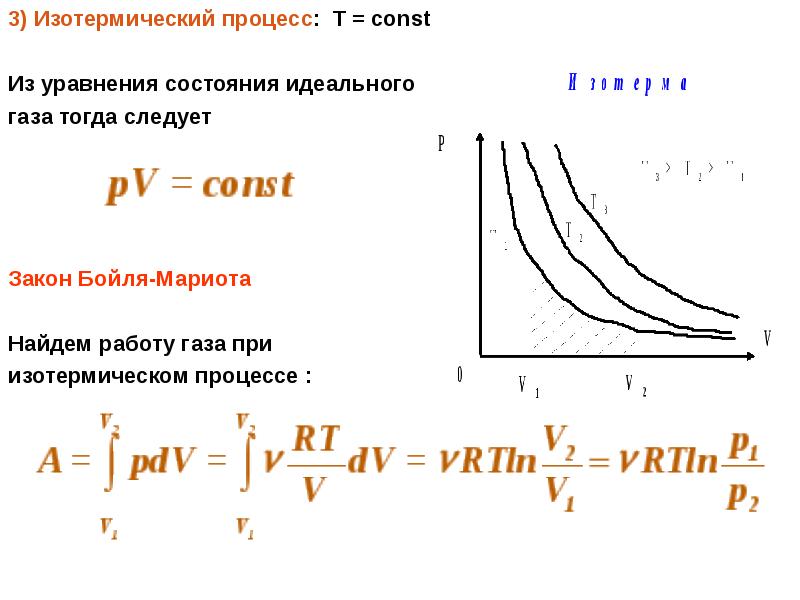
- 5. 3) Изотермический процесс: Т = const 3) Изотермический процесс: Т =
- 6. Используя формулу U = сVT , получаем Используя формулу U =
- 7. 4) Адиабатический процесс : d'Q = 0 4) Адиабатический процесс :
- 8. Исключая dT , получаем
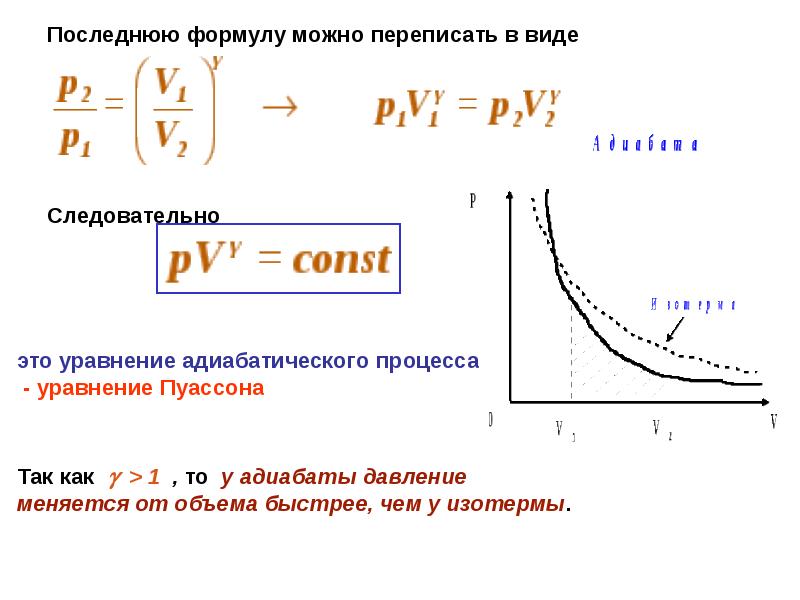
- 9. Последнюю формулу можно переписать в виде Последнюю формулу можно переписать в
- 10. Используя уравнение состояния идеального газа, преобразуем уравнение Пуассона к виду
- 11. Найдем работу газа при адиабатическом процессе. Найдем работу газа при
- 12. Тогда Тогда Используя
- 13. 11.6 Политропические процессы 11.6 Политропические процессы Политропический процесс – это процесс
- 14. С другой стороны, из уравнения состояния идеального газа С другой стороны,
- 15. Обозначим
- 16. Изменение энтропии в неадиабатических процессах идеального газа Изменение энтропии в неадиабатических
- 17. Поэтому изменение энтропии на конечном участке процесса между состояниями 1 и
- 18. Отсюда следует, что Отсюда следует, что 1 ) при
- 19. Изменение энтропии при плавлении и испарении Изменение энтропии при плавлении и
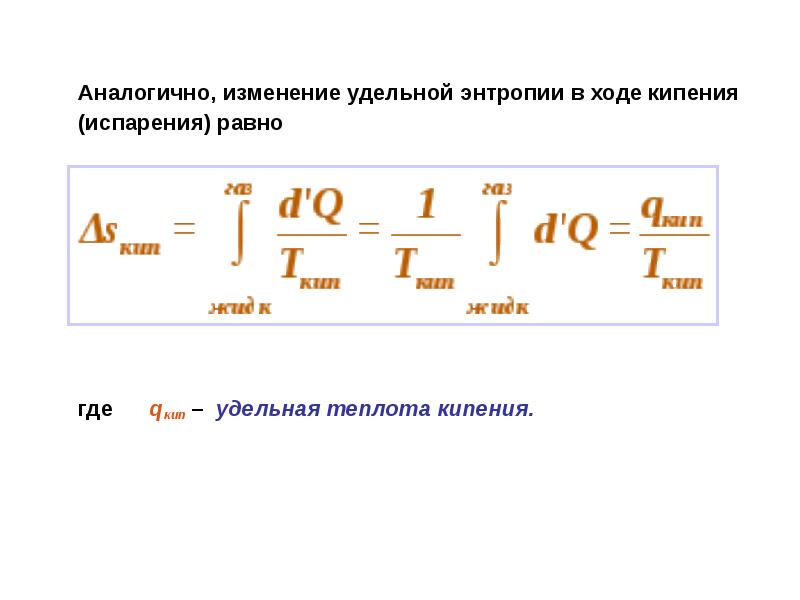
- 20. Аналогично, изменение удельной энтропии в ходе кипения (испарения) равно
- 21. В сосуде под поршнем находится масса m=1г азота. Какое количество теплоты
- 22. Скачать презентацию




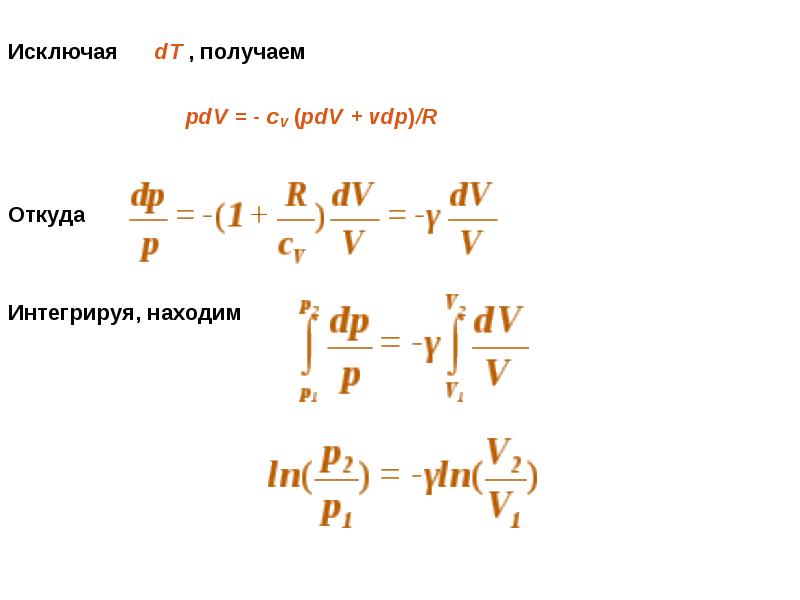











Слайды и текст этой презентации
Скачать презентацию на тему Применение первого начала термодинамики к изопроцессам можно ниже:
Похожие презентации