Топологические изоляторы и смежные вопросы презентация
Содержание
- 2. План лекций Лекция 1 -
- 3. Что такое топологич. изолятор - 1 Простейший пример: зонный диэлектрик (3-мерный
- 4. Предистория:
- 6. Гамильтониан поверхностных электронных состояний H = v0(-i∂ - eA)σ + geffσB
- 7. Сравним с графеном: один «дираковский» фермион вместо 4-х в графене (там
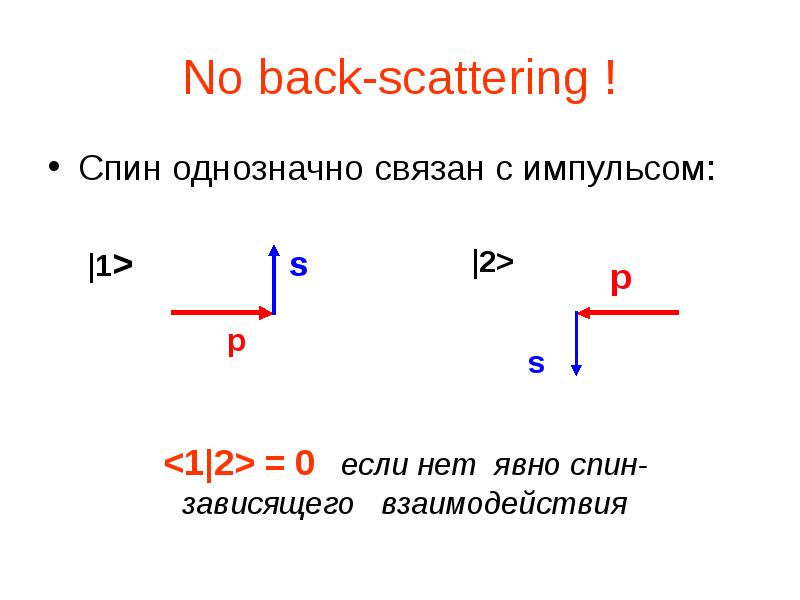
- 10. No back-scattering ! Спин однозначно связан с импульсом:
- 11. Что такое топологич. изолятор - 2 Электродинамика с Ө-членом:
- 12. Что будет при Ө ≠ CONST ?
- 13. Магнито-электрический эффект
- 14. “Dynamical Axion Field in Topological Magnetic Insulators” R. Li, J. Wang,
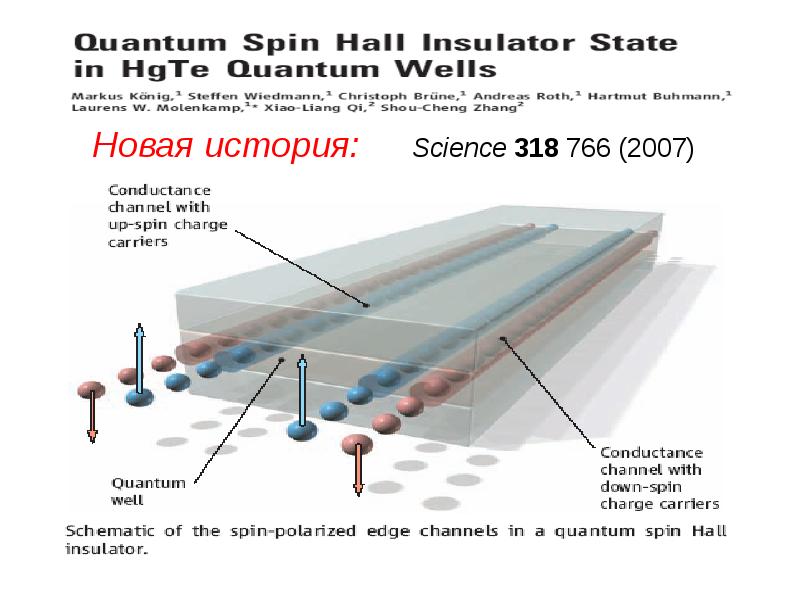
- 15. Объекты, известные как Топологические Изоляторы или Топ. Сверхпроводники 2D: HgTe (квантовые
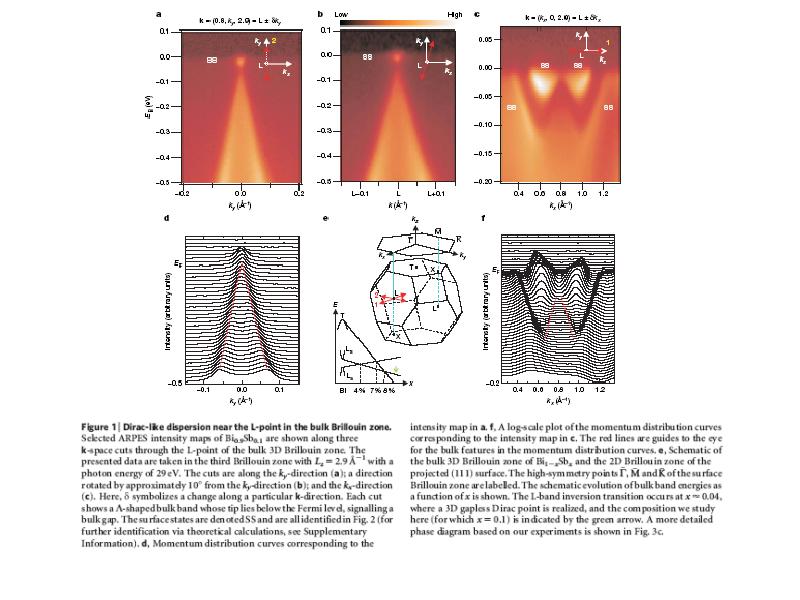
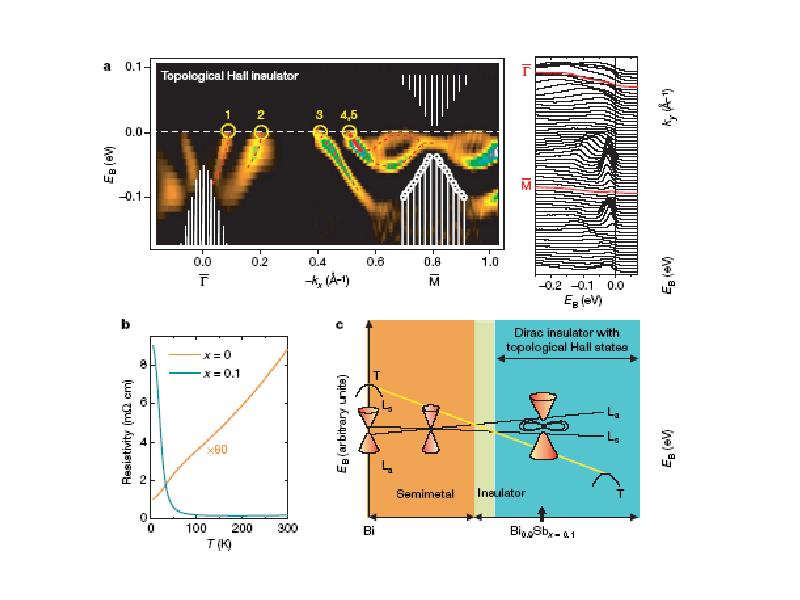
- 16. Эксперименты ARPES
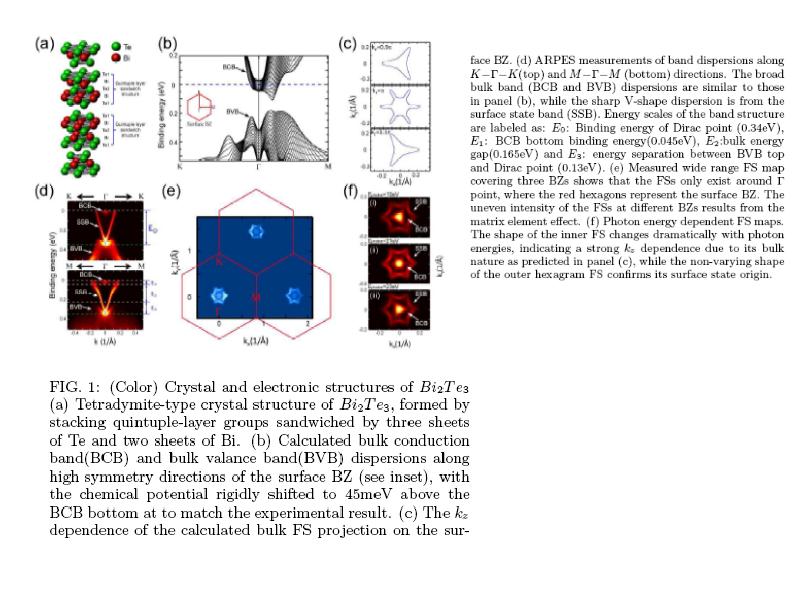
- 22. Large Gap Topological Insulator Bi2Te3 with a Single Dirac Cone on
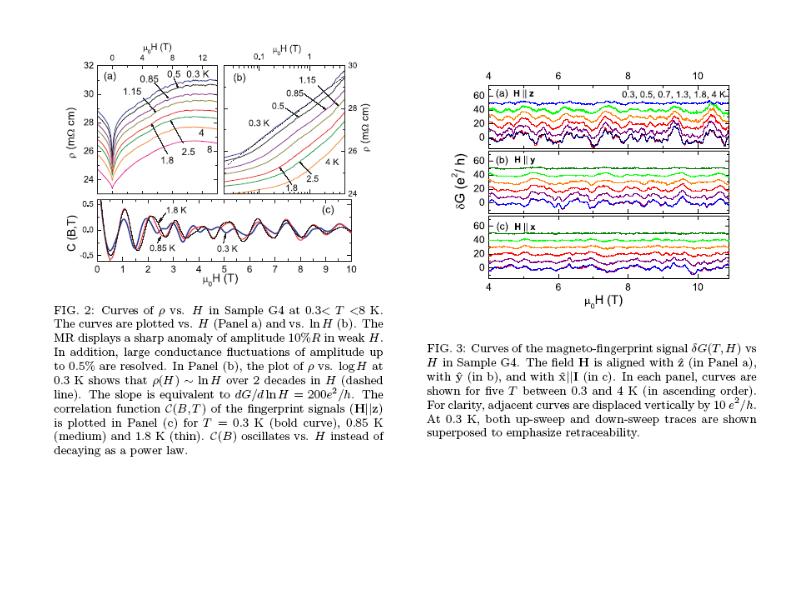
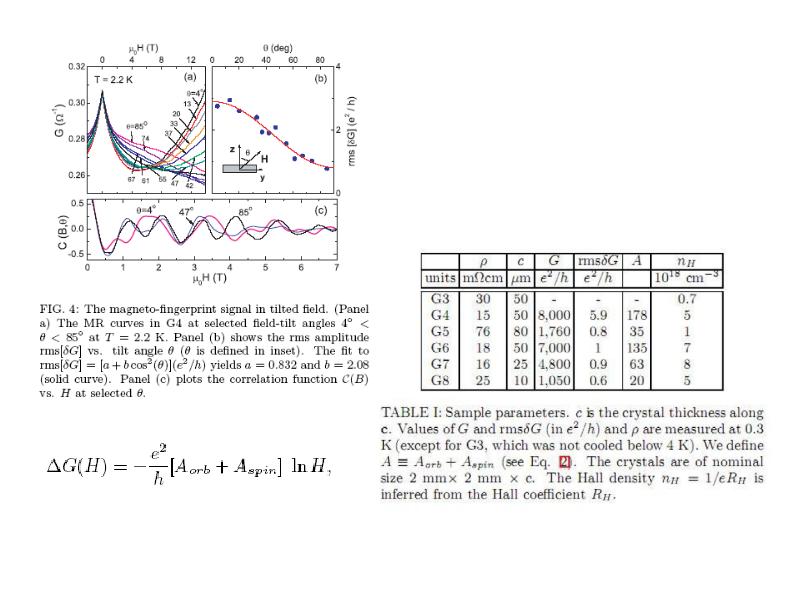
- 26. Транспортные эксперименты
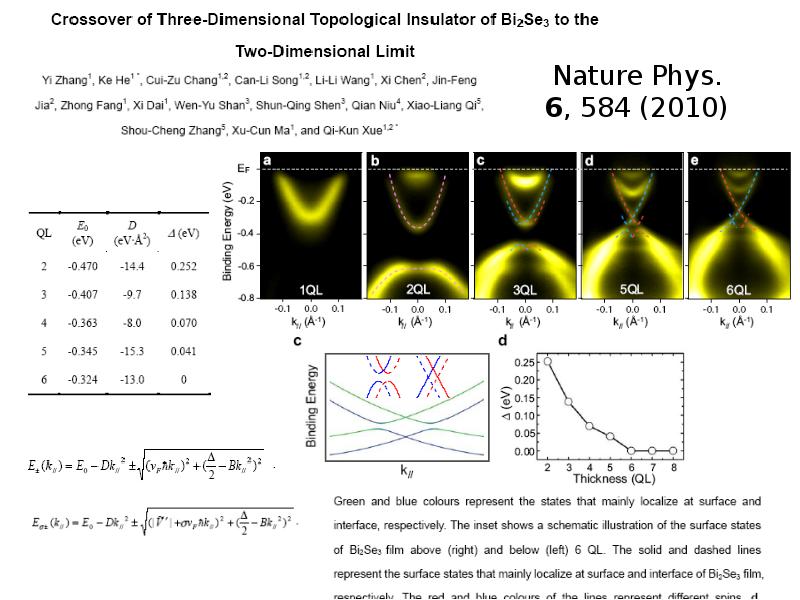
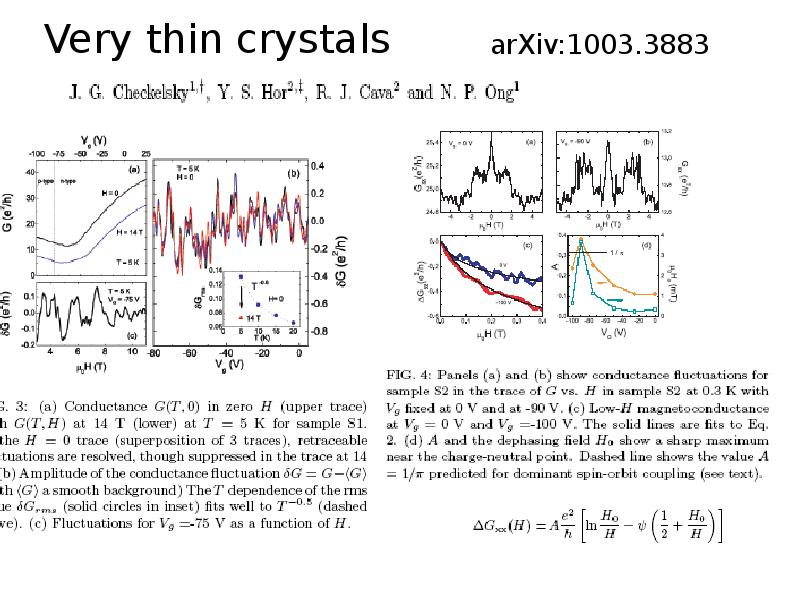
- 32. Very thin crystals
- 34. Лекция 2. Теория Топологические свойства зонных диэлектриков Общая классификация возможных топологических
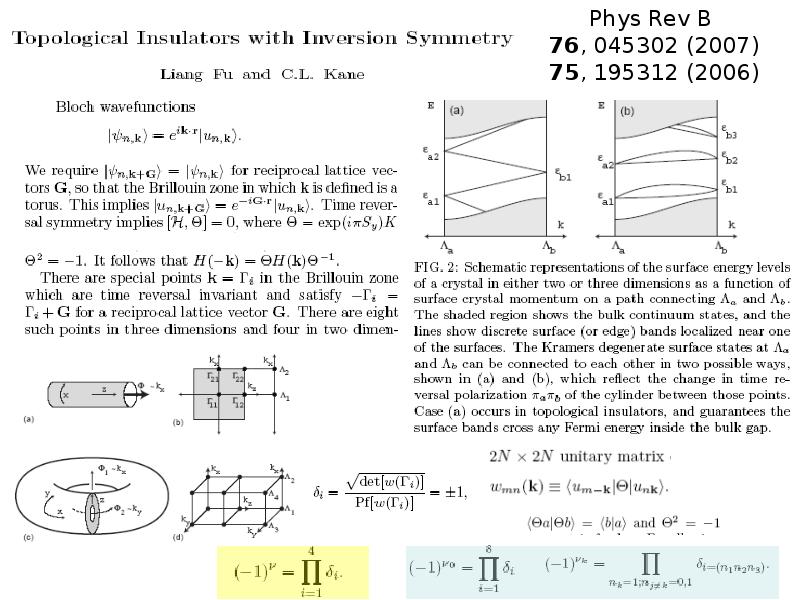
- 35. Теория зонных ТИ
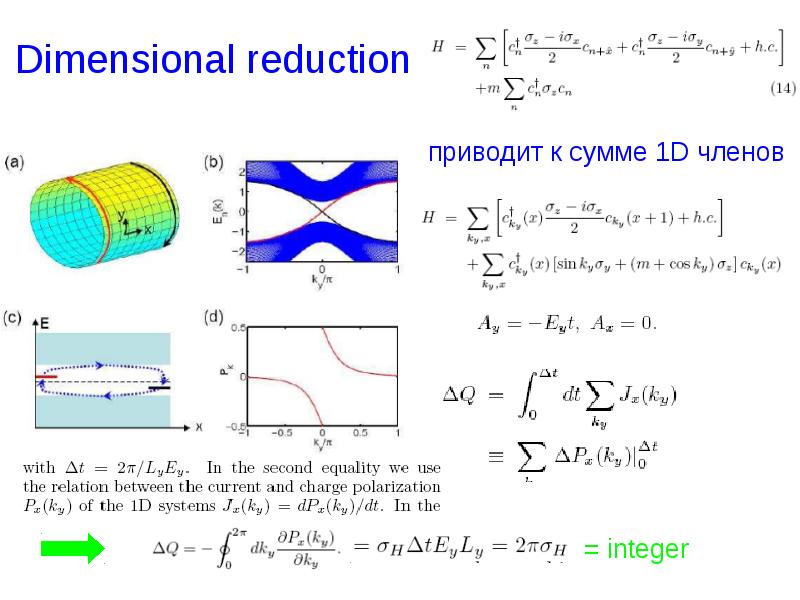
- 39. Dimensional reduction
- 42. Туннель для связи с антиподами Тонкая бесконечная пластинка ТИ На верхней
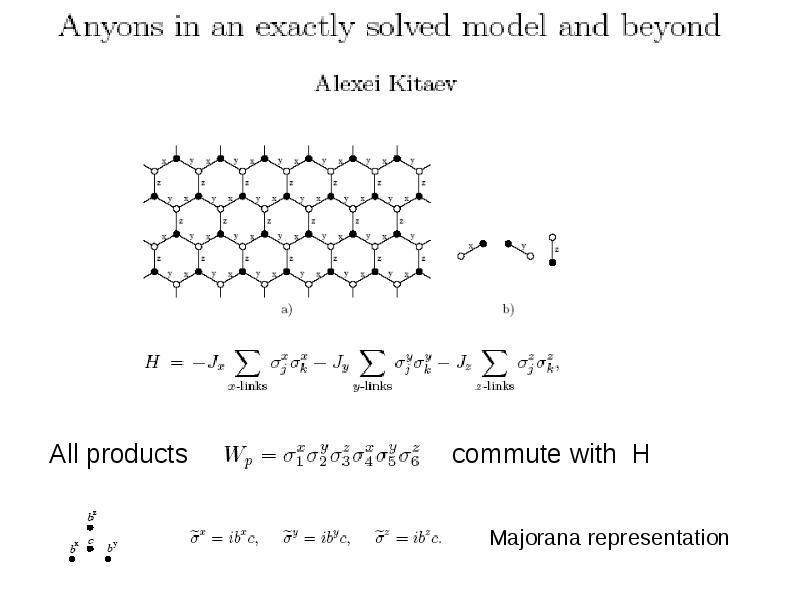
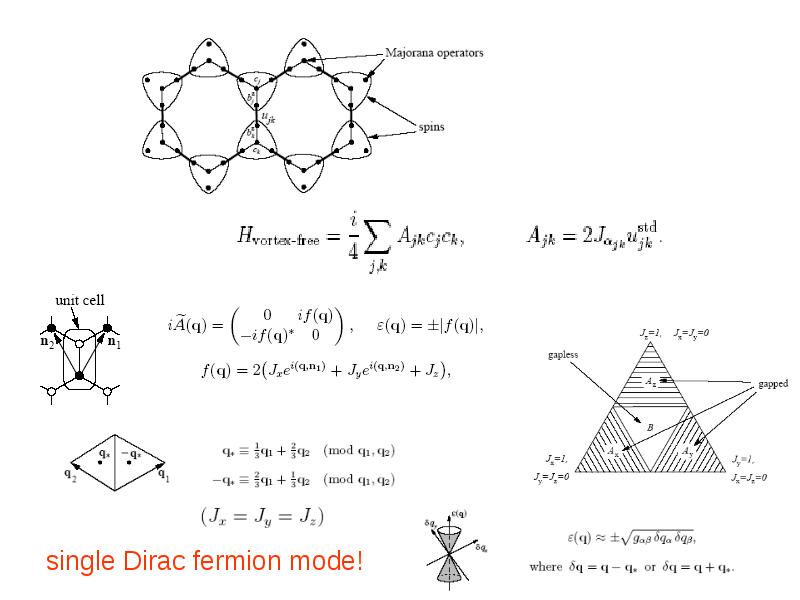
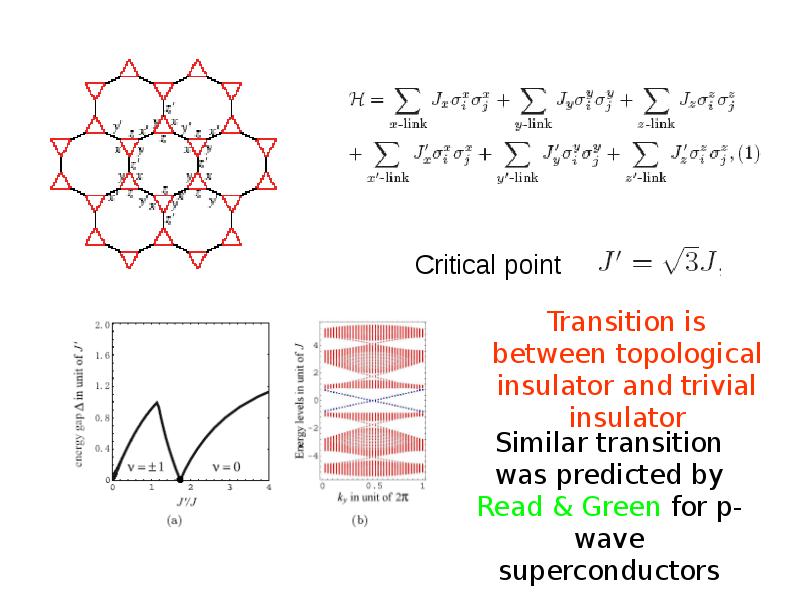
- 44. Connections to spin-liquids and p+ip superconductors Основы:
- 47. B-phase can be made gapful 1) Including of magnetic field, or
- 49. Майорановские состояния в центрах сверхпроводящих вихрей и неабелева обменная статистика
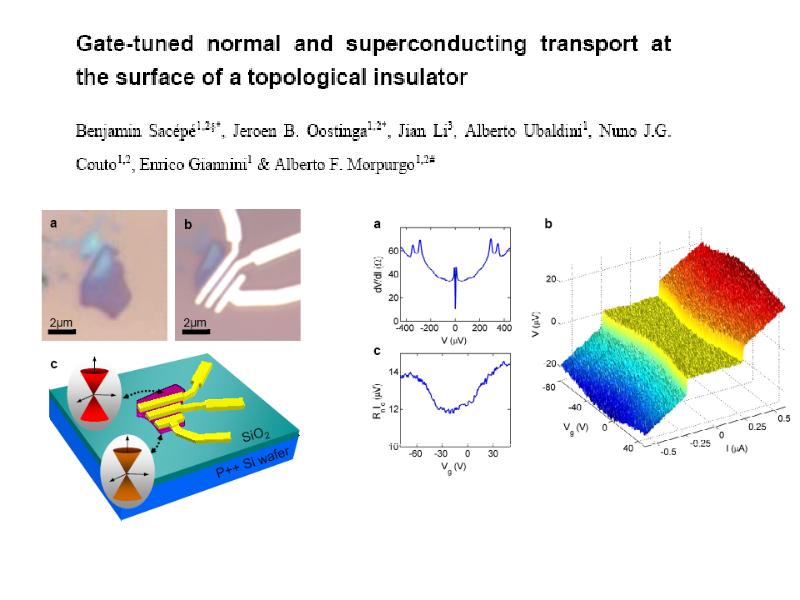
- 50. Superconducting Proximity Effect and Majorana Fermions at the Surface of a
- 51. Аналогия (неполная) с px+ipy сверхпроводником
- 52. Сверхпроводящий эффект близости на поверхности ТИ С учетом примесного рассеяния
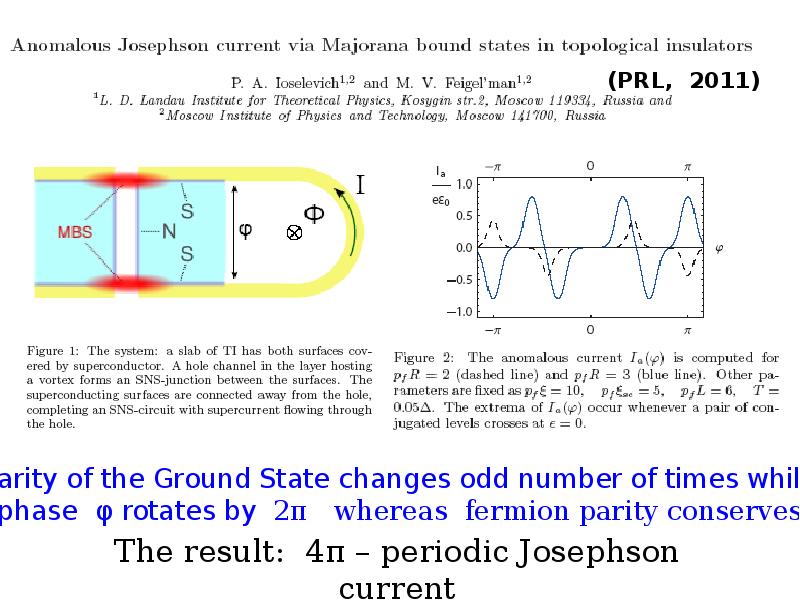
- 53. Индуцированная сверхпроводимость и майорановские состояния Superconducting Proximity Effect and Majorana Fermions
- 56. Скачать презентацию


















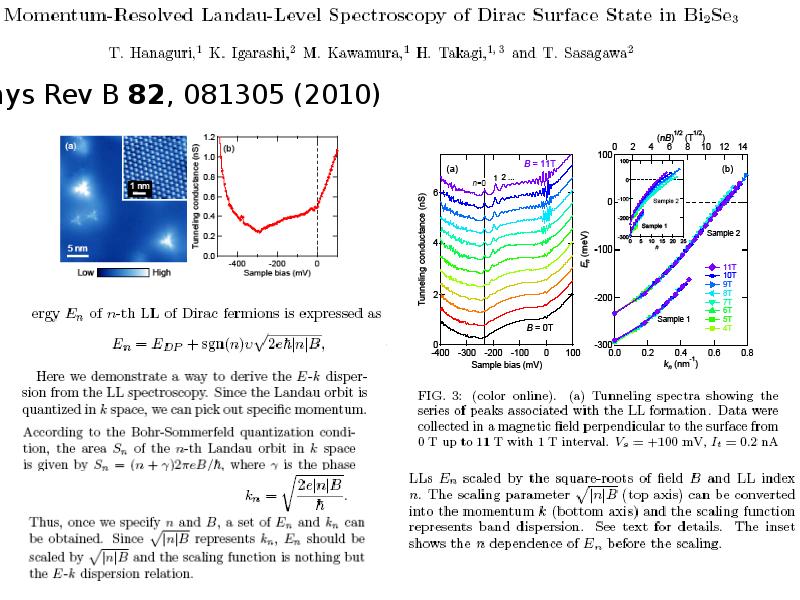

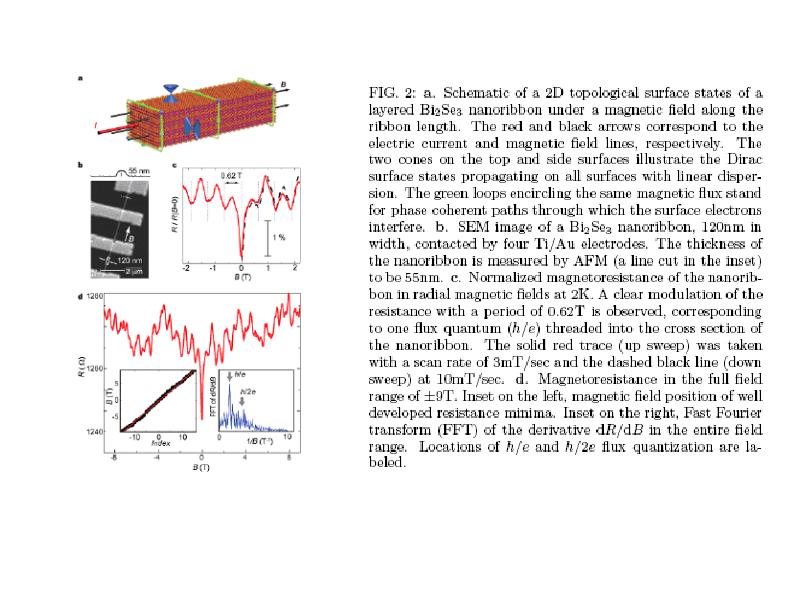
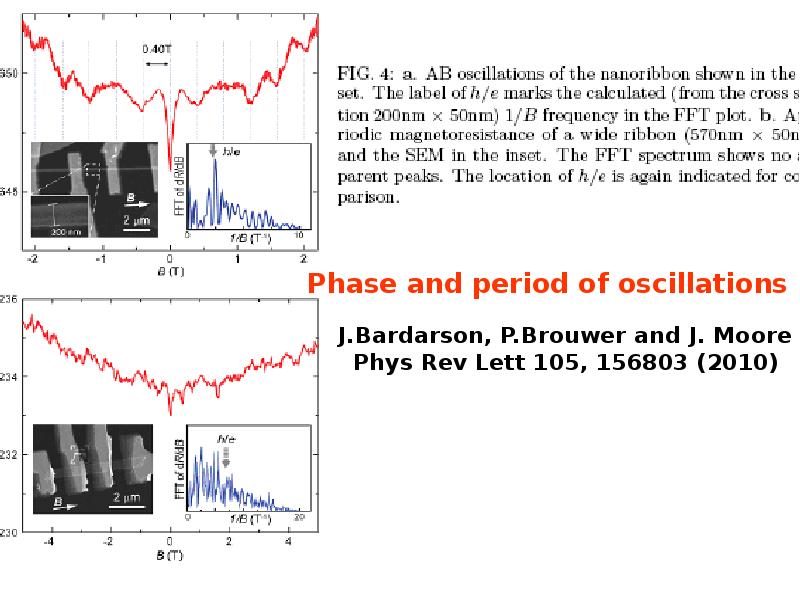
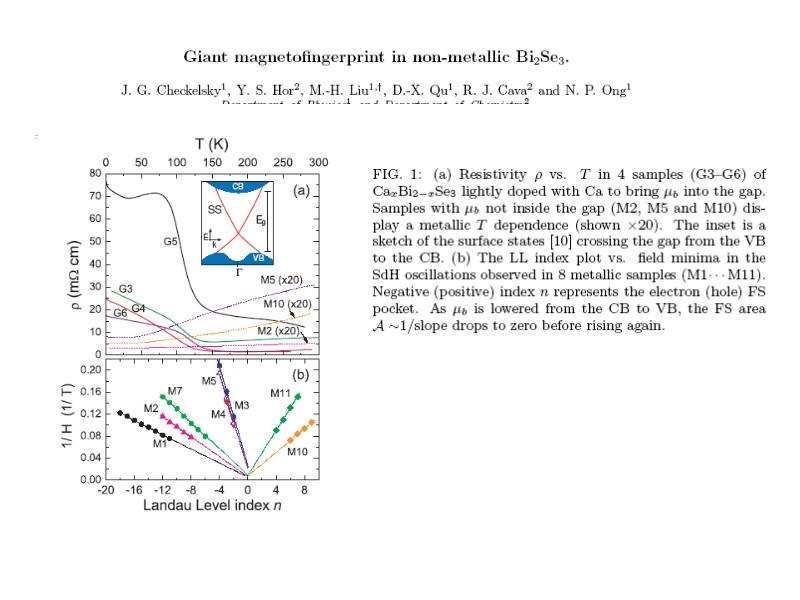
















Слайды и текст этой презентации
Скачать презентацию на тему Топологические изоляторы и смежные вопросы можно ниже:
Похожие презентации