Уравнение Шрёдингера, волновая функция презентация
Содержание
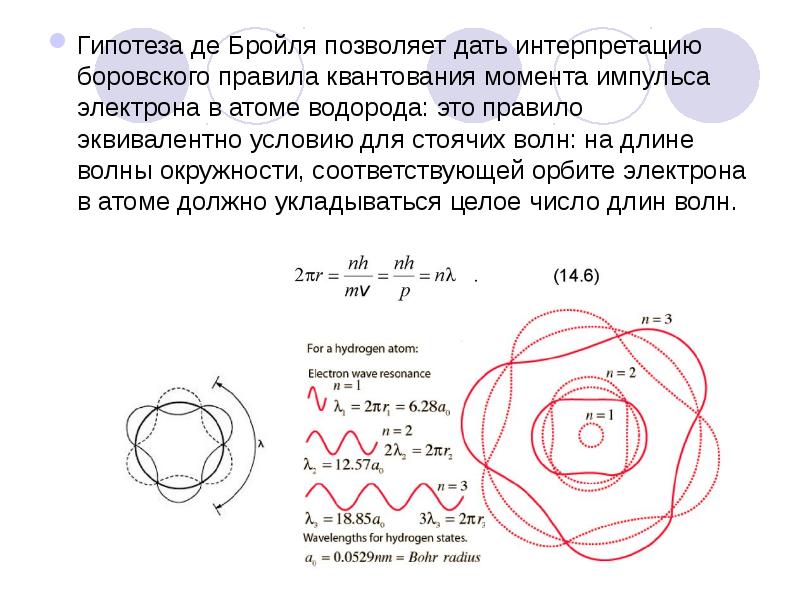
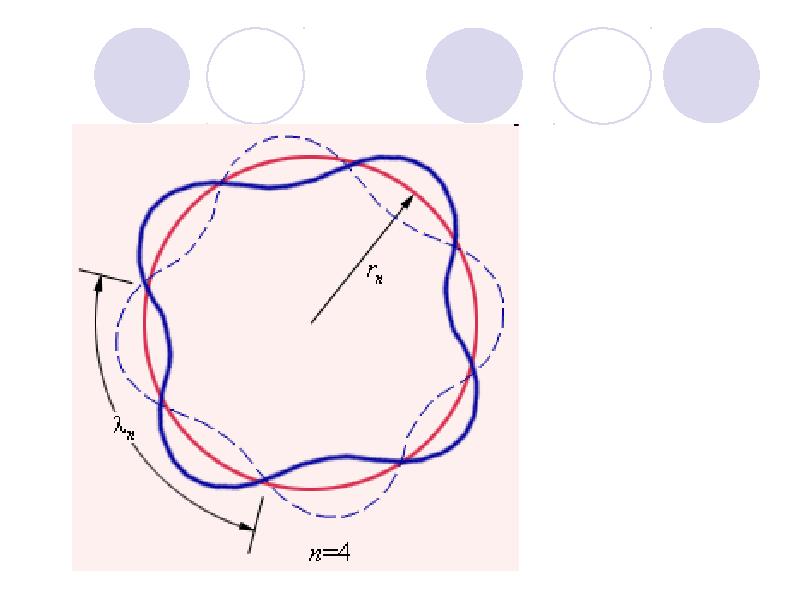
- 3. Гипотеза де Бройля позволяет дать интерпретацию боровского правила квантования момента импульса
- 7. Уравнение Шрерингера
- 8. Квантовые операторы − символические изображения математических операций преобразования величин в
- 9. Например: оператор может означать дифференцирование по какой-либо переменной Например: оператор
- 10. Примеры некоторых операторов Оператор координаты равен самой координате x,
- 11. Энергия частицы массой имеет две составляющие – кинетическую и потенциальную:
- 12. Свободная частица массы m0: Свободная частица массы m0:
- 13. Примеры некоторых гамильтонианов Частица в одномерной потенциальной яме U(x), 0 <
- 14. Кинетическая энергия Если заменить в правой части уравнения величину импульса
- 15. операторы проекций импульсов
- 16. уравнения для собственных функций и собственных значений операторов проекций импульсов
- 17. Решением первого уравнения системы является волновая функция
- 18. Уравнение Шредингера для свободной частицы Решения уравнения Шрёдингера существуют только для
- 19. Уравнение Шредингера для свободной частицы В стационарном случае Шредингер заметил, что
- 21. Учитывая потенциальную энергию электрона Учитывая потенциальную энергию электрона Это
- 24. Волновая функция
- 25. Решения в виде стоячей волны зависят от времени благодаря множителю
- 26. Волновая функция
- 27. Волновая функция
- 28. Как определить саму волновую функцию? в соответствии с соотношением неопределенностей
- 29. Ве́рнер Карл Ге́йзенберг Ве́рнер Карл Ге́йзенберг (нем. Werner Karl Heisenberg; 5 12 1901 — 1
- 32. Максимум, что можно сделать – это определить три координаты или три
- 33. Так что такое волновая функция? В 1926 г. немецкий физик
- 34. Макс Борн Макс Борн (нем. Max Born; 1112 1882 - 5 01 1970) — немецкий
- 35. Волновая функция Шредингеровская волновая функция (амплитуда волны де Бройля) определяет вероятность
- 36. Вероятность обнаружить данную частицу в объеме dV здесь
- 38. Для свободной частицы =0
- 39. Если взять волну де Бройля, идущую в сторону положительных значений оси
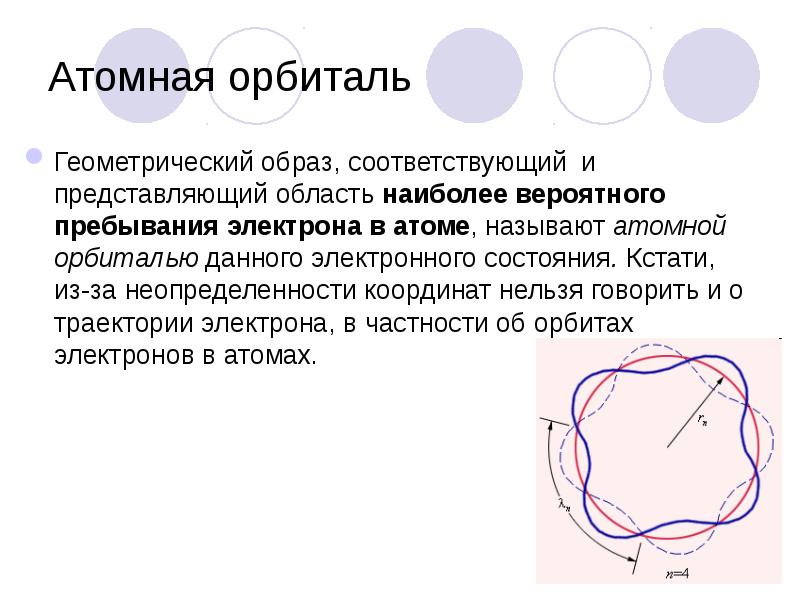
- 40. Атомная орбиталь Геометрический образ, соответствующий и представляющий область наиболее вероятного пребывания
- 41. При условии стационарности поля внешних сил (
- 42. После разделения переменных можно получить два уравнения для временной и координатной
- 43. Решение уравнения с точностью до множителя С будет иметь во всех
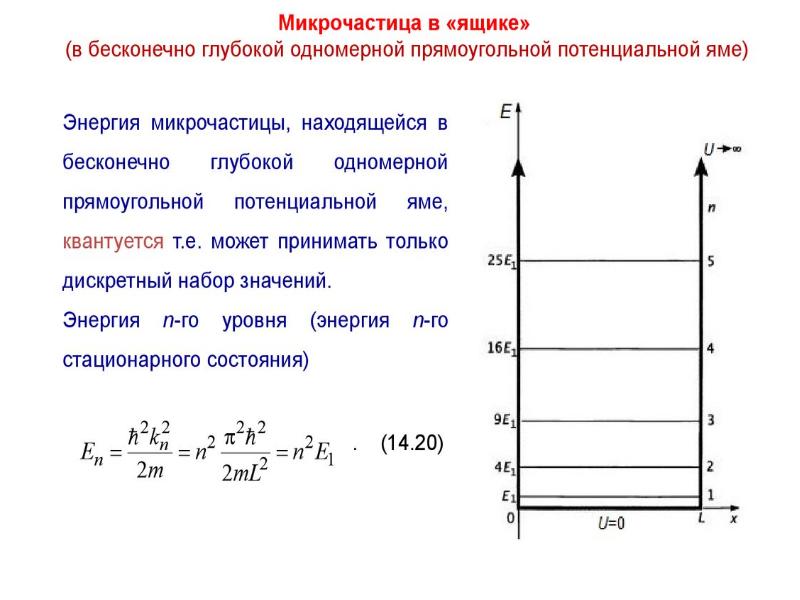
- 45. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Вводя обозначение
- 46. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Заметим, что условие
- 48. Решение уравнение Шредингера частицы, находящейся в потенциальной яме
- 49. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Случай п=0 следует
- 50. Решение уравнение Шредингера частицы, находящейся в потенциальной яме
- 51. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Как энергия состояния,
- 52. Решение уравнение Шредингера частицы, находящейся в потенциальной яме Каждому значению соответствует
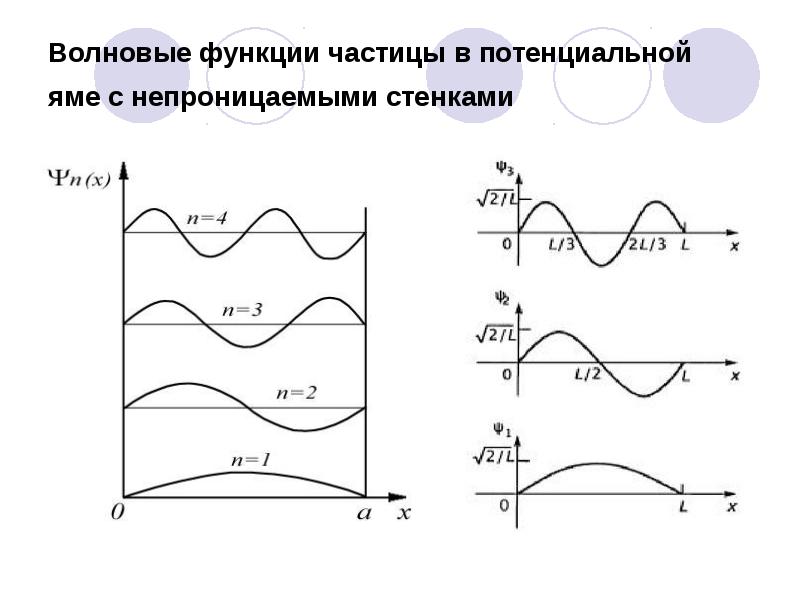
- 53. Волновые функции частицы в потенциальной яме с непроницаемыми стенками
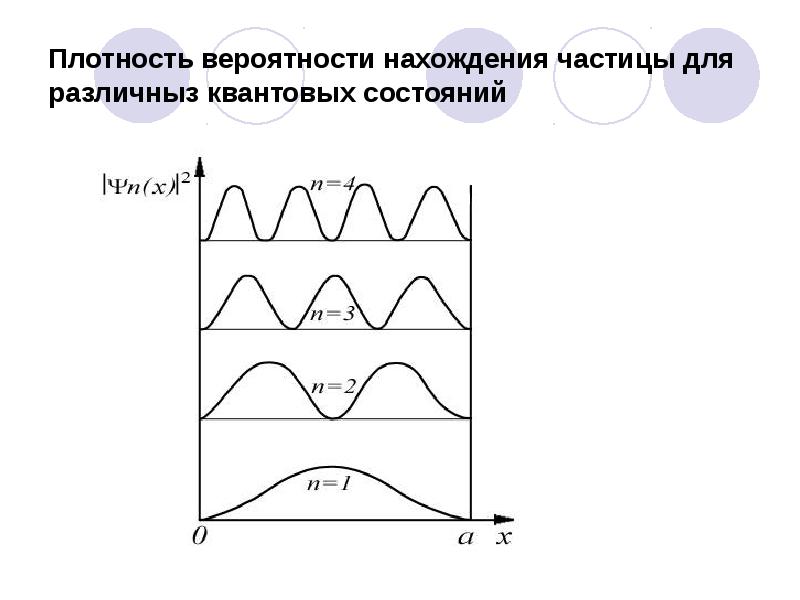
- 54. Плотность вероятности нахождения частицы для различныз квантовых состояний
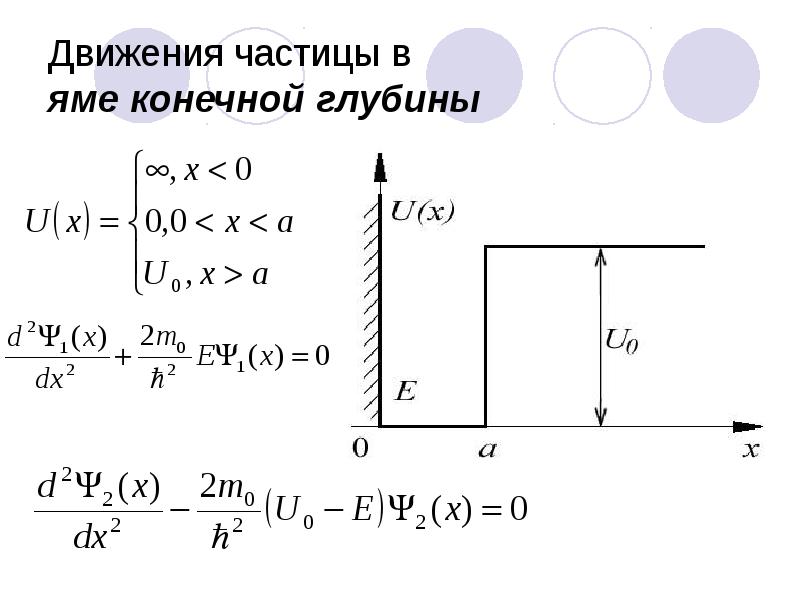
- 55. Движения частицы в яме конечной глубины
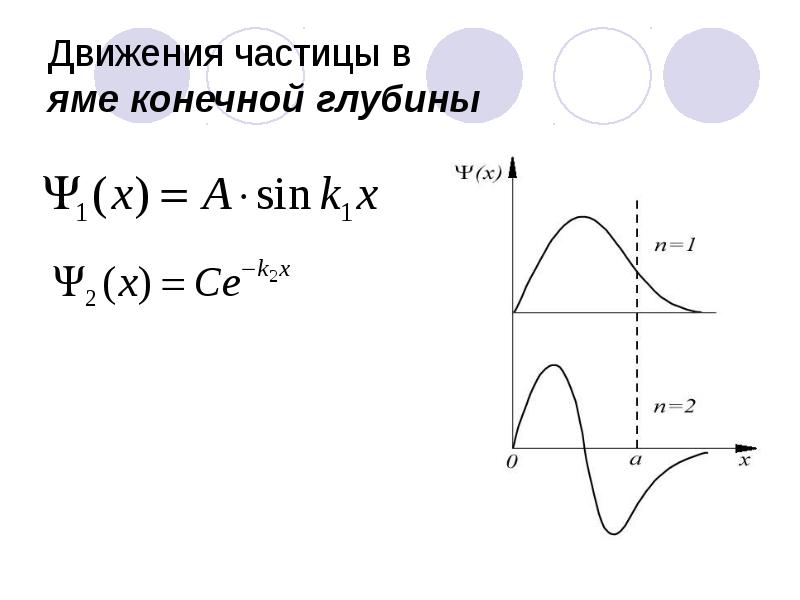
- 56. Движения частицы в яме конечной глубины
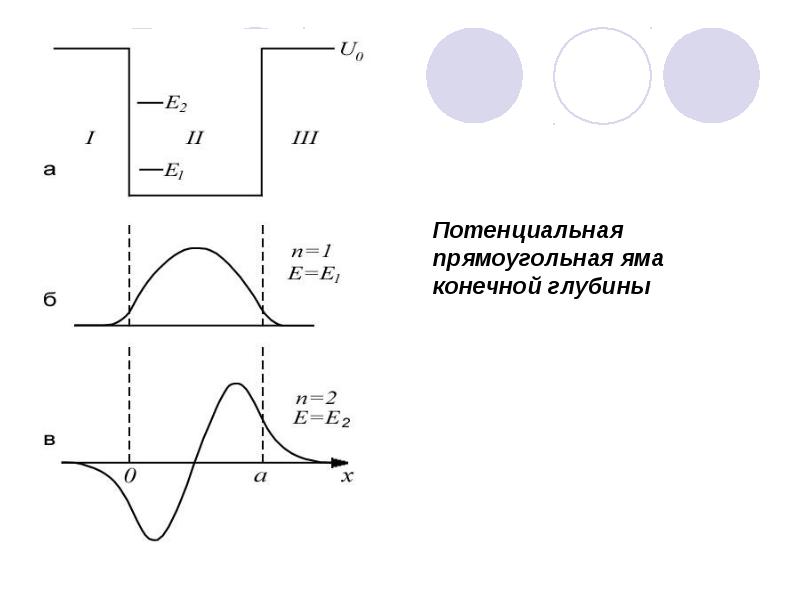
- 57. Потенциальная прямоугольная яма конечной глубины
- 58. Потенциальная прямоугольная яма конечной глубины
- 59. Туннельный эффект Как было показано, решение уравнения Шредингера для свободной
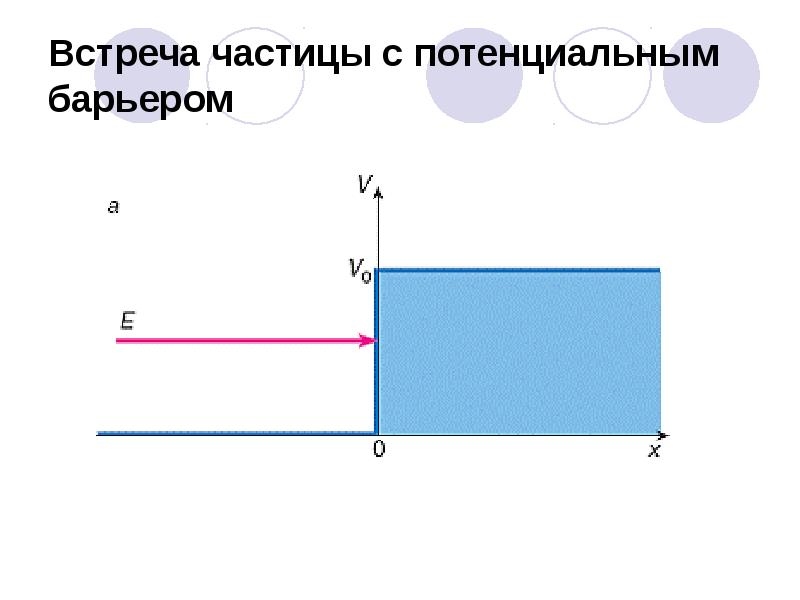
- 60. Встреча частицы с потенциальным барьером
- 61. Встреча частицы с потенциальным барьером В рамках классической механики априорно ясно,
- 62. Встреча частицы с потенциальным барьером Туннельный эффект является принципиально квантово-механическим эффектом,
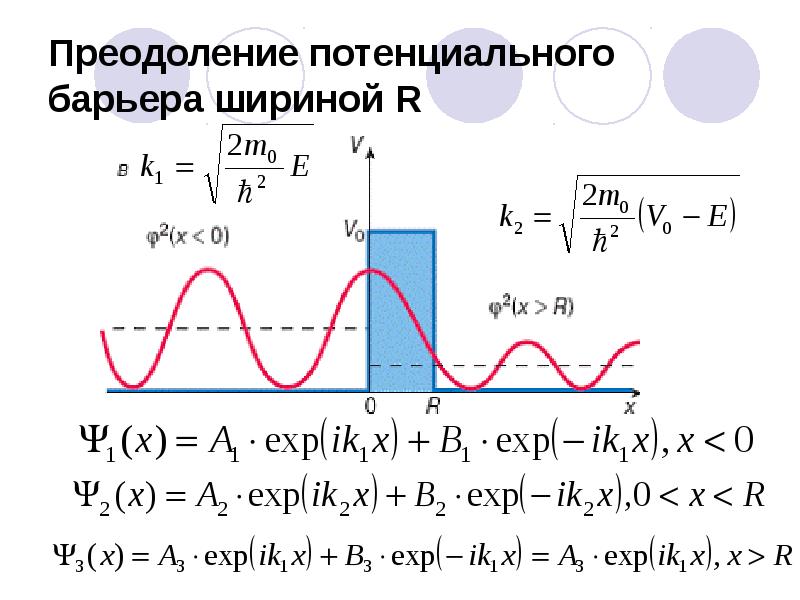
- 63. Преодоление потенциального барьера шириной R
- 64. Преодоление потенциального барьера шириной R Отношение квадратов модулей амплитуд отраженной и
- 65. Коэффициент прохождения D (коэффициент прозрачности), определяющий часть потока частиц, прошедшего
- 66. Встреча частицы с потенциальным барьером Рассмотрение случая высокого потенциального барьера (
- 67. Полагая В2=0 (отражением от второй границы барьера можно пренебречь при условии
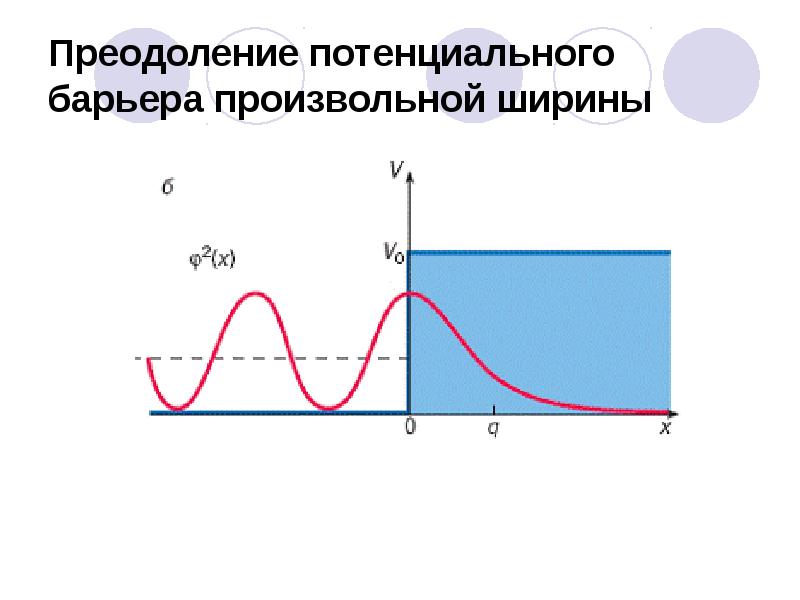
- 68. Преодоление потенциального барьера произвольной ширины
- 69. Можно показать, что для высокого потенциального барьера любой формы коэффициент прозрачности
- 70. Вероятность туннелирования уменьшается с ростом ширины барьера, его высоты (точнее, разности
- 71. Основы теории туннельных переходов заложены работами советских ученых Л.И. Мандельштама и
- 72. Квантовый осциллятор Известно, что гармонический осциллятор, то есть система, совершающая
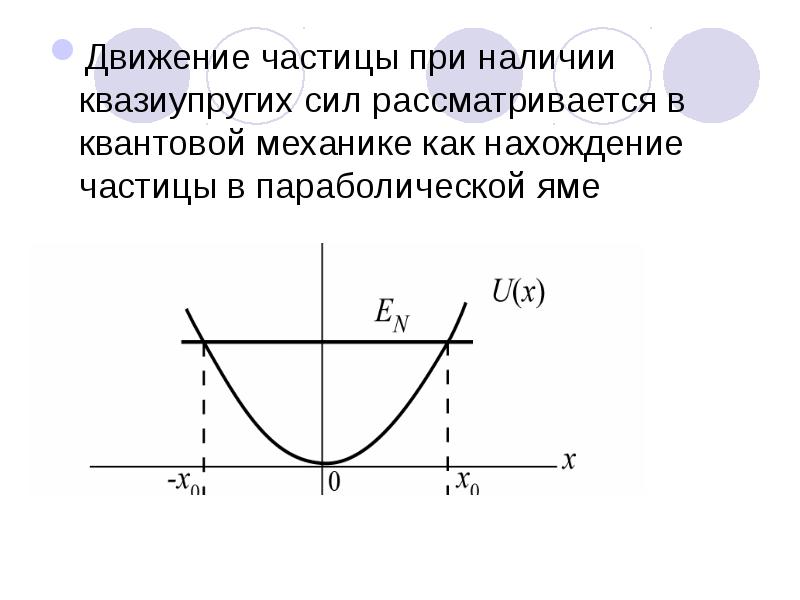
- 73. Движение частицы при наличии квазиупругих сил рассматривается в квантовой механике как
- 74. Гамильтониан для потенциальной Гамильтониан для потенциальной энергии
- 75. Вводя величины Вводя величины
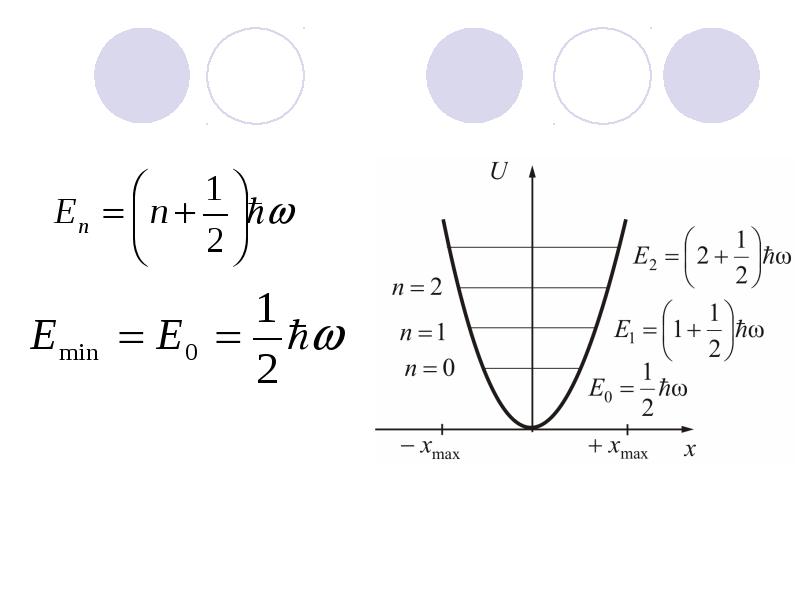
- 77. Отметим, что уровни гармонического квантового осциллятора, в отличие от случая прямоугольной
- 78. Приведем вид волновых функций для первых трех энергетических уровней гармонического осциллятора:
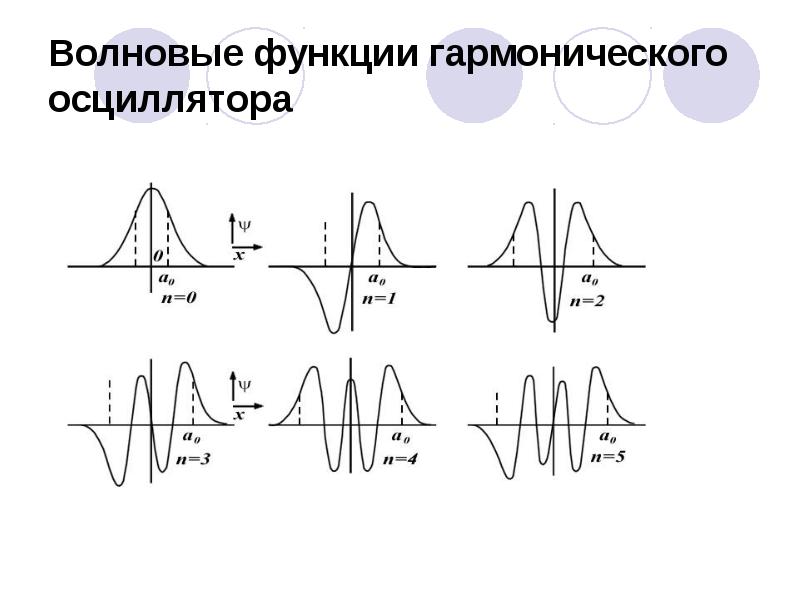
- 79. Волновые функции гармонического осциллятора
- 80. Отметим, что вне классической области Отметим, что вне классической области волновые
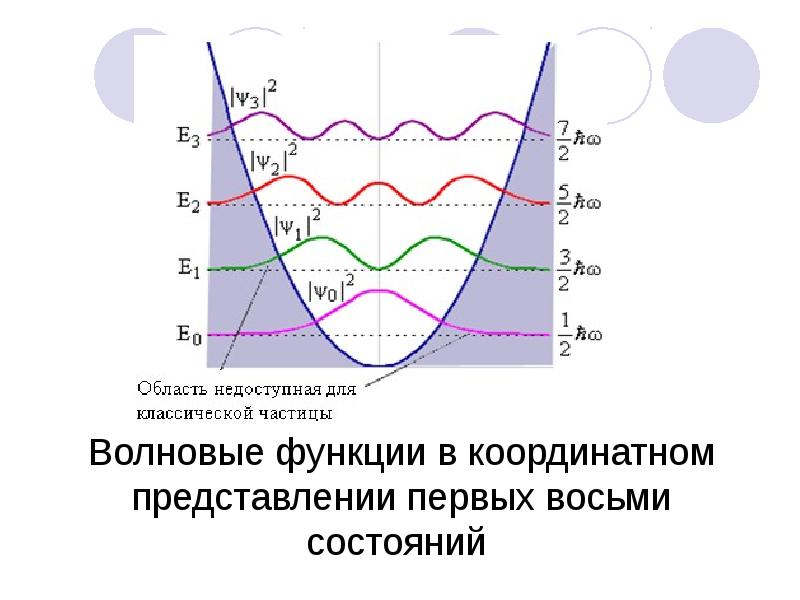
- 81. Волновые функции в координатном представлении первых восьми состояний
- 88. Скачать презентацию







































































Слайды и текст этой презентации
Скачать презентацию на тему Уравнение Шрёдингера, волновая функция можно ниже:
Похожие презентации