Введение в физику. (Лекция 1) презентация

Лекции по физике Второй семестр 2017-2018 годов

Лекции по физике Лектор – Леонид Константинович Попов Электронный адрес: lkpopov@ngs.ru Расписание: Аудитории 3113, 2120 Четверг - 9-00, Пятница (знаменатель)- 12-40 Семинары: 3 семинара в 2 недели

Катунь-Еландинский порог

Лекции по физике Программа Курса в текущем семестре: Основы классической механики – 12 лекций –февраль-март. 2. Термодинамика и молекулярная физика – 12 лекций апрель-май.

Лекции по физике Формы проверки знаний Одно семестровое задание, состоящее из двух частей. Две контрольных работы. Экзамен.

Литература - учебники Л.А. Лукьянчиков. Механика. Молекулярная физика. НГУ, 2007 г. Д.В. Сивухин. Курс общей физики. Т. 1. Механика. М., «Наука» 1989 г. Д.В. Сивухин. Курс общей физики. Т. 2. Термодинамика и молекулярная физика. 1990 г. И.Е. Иродов. Механика. Основные законы. М. Высшая школа. 1985 г.

Литература - задачники Задачи по общей физике для геологов. НГУ 2000 г. С.П. Стрелков, Д.В. Сивухин, В.А. Угаров, И.А. Яковлев. Сборник задач по общему курсу физики. М. 1977 г. Д.В.Сивухин. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика. М., «Наука» 1976 г. И.Е. Иродов. Задачи по общей физике. М., «Наука» 1979 г. В.С. Волькенштейн. Сборник задач по общему курсу физики. М., «Наука» 1985 г.

Линия старта

Лекция 1. Введение Слово «физика» (φύσις ) в греческом языке означает «природа». Этот термин впервые ввел Аристотель (384-322 гг. до н.э). Его учение пользовалось незыблемым авторитетом более 1500 лет. Предметом физики и является материя (в виде вещества и полей) и наиболее общие формы её движения, а также фундаментальные взаимодействия, управляющие движением материи.

Физика и математика Математика предоставляет аппарат, с помощью которого физические законы могут быть точно сформулированы. Физические теории почти всегда формулируются в виде математических выражений. Развитие математики стимулировалось потребностями физических теорий.

Физика и геология Проблемы геологии, теснейшим образом связанные с физикой: происхождение Земли и других планет; строение и состав различных геосфер; возраст Земли и датирование этапов её развития; термическая история Земли; разработка теории разрушения горных пород; прогноз геодинамических процессов (землетрясения, горные удары, внезапные выбросы газов и др.).

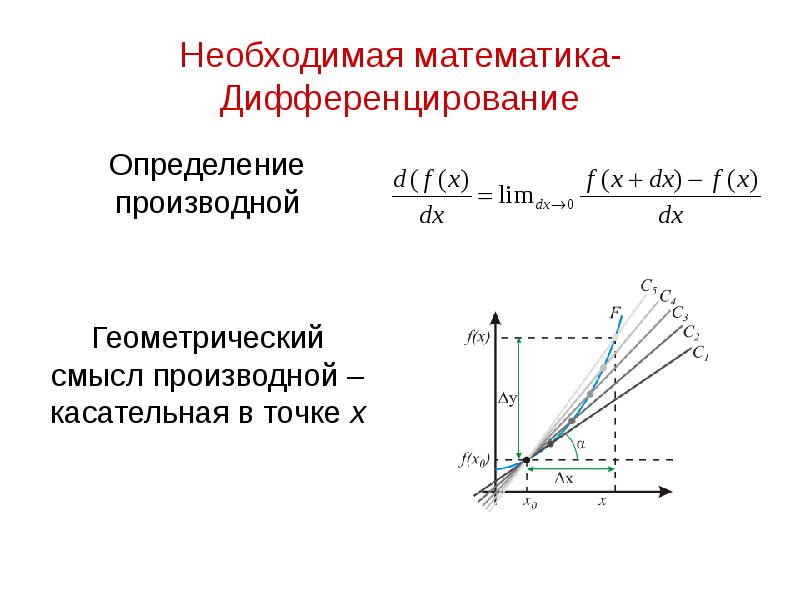
Необходимая математика-Дифференцирование Определение производной Геометрический смысл производной – касательная в точке x

Необходимая математика-Дифференцирование Правила Дифференцирования

Необходимая математика-Дифференцирование Примеры производных

Необходимая математика-Интегрирование Определение интеграла Определенный интеграл как площадь под кривой

Необходимая математика-Интегрирование Вычисление определенного интеграла Таблица неопределенных интегралов

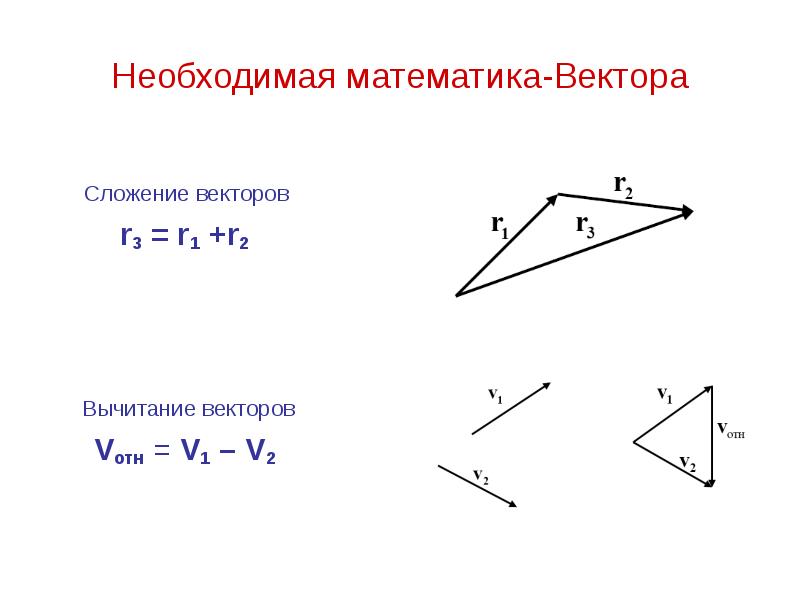
Необходимая математика-Вектора Сложение векторов r3 = r1 +r2 Вычитание векторов Vотн = V1 – V2

Необходимая математика-Вектора Для векторов создана векторная алгебра. b = c a- умножение на число c = a+b – сложение; с =a -b – вычитание; c =(ab)= |a||b|cos - скалярное умножение (с - скаляр, т.е. число,  - угол между направлениями векторов). С=[ab]=a×b = - векторное умножение С=absin()

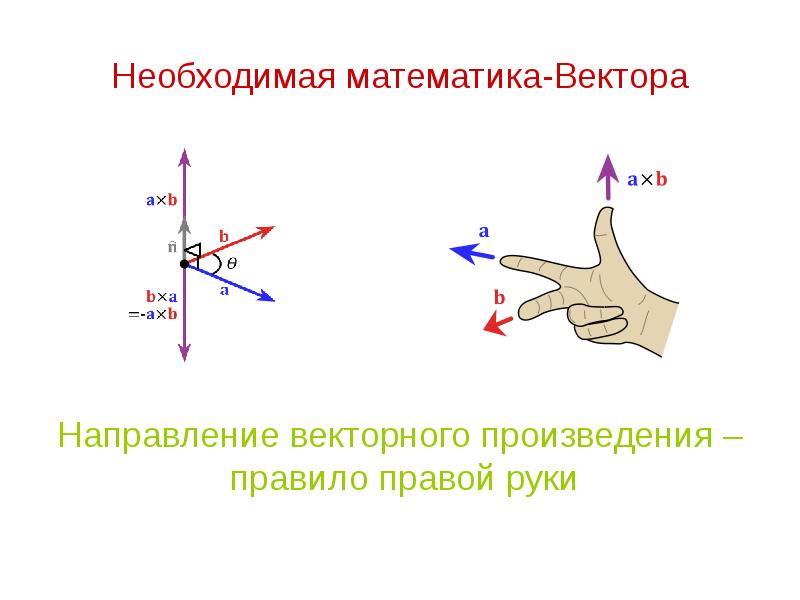
Необходимая математика-Вектора Направление векторного произведения – правило правой руки

Механика как раздел физики Механика есть наука о движении и равновесии тел и частиц.

Исаак Ньютон – основоположник механики Принципы классической механики впервые были сформулированы Ньютоном (1642-1727) в его основном сочинении «Математические начала натуральной философии», первое издание которого вышло 1687 году. До начала двадцатого века эти принципы практически не изменялись.

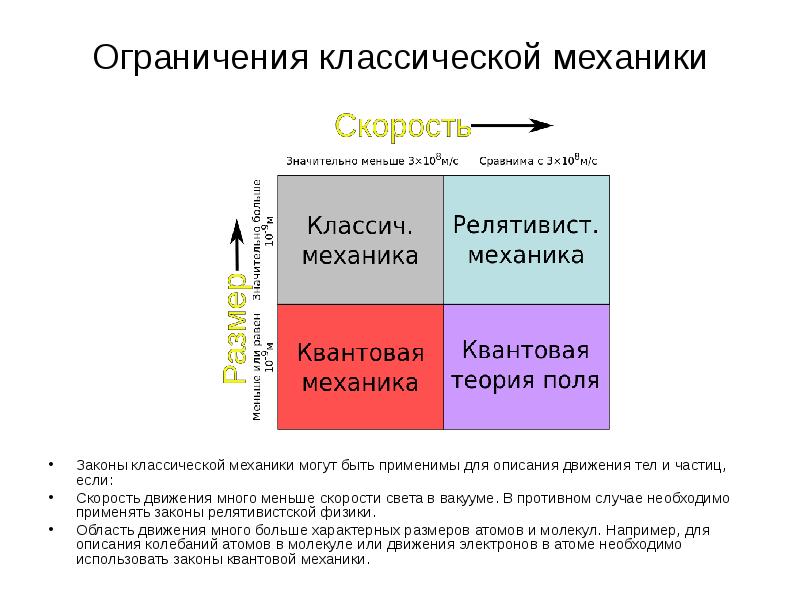
Ограничения классической механики Законы классической механики могут быть применимы для описания движения тел и частиц, если: Скорость движения много меньше скорости света в вакууме. В противном случае необходимо применять законы релятивистской физики. Область движения много больше характерных размеров атомов и молекул. Например, для описания колебаний атомов в молекуле или движения электронов в атоме необходимо использовать законы квантовой механики.

Кинематика Кинема́тика - раздел механики, изучающий математическое описание движения идеализированных объектов без рассмотрения причин движения. Исходные понятия кинематики - пространство и время.

Свойства пространства Пространство однородно. Все точки в нем равноправны

Свойства пространства Пространство изотропно. Все направления в нем равноправны

Свойства пространства Пространство Евклидово. Параллельные прямые не пересекаются, сумма углов всегда треугольника равна 

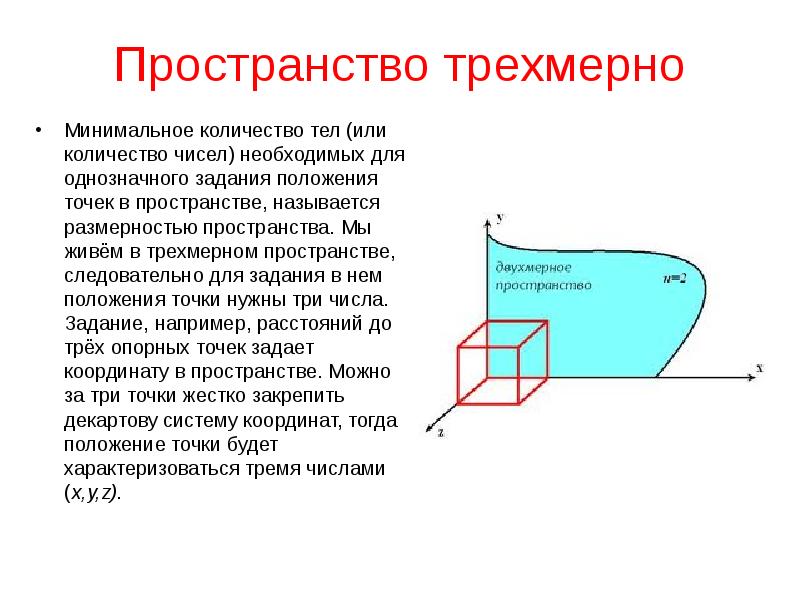
Пространство трехмерно Минимальное количество тел (или количество чисел) необходимых для однозначного задания положения точек в пространстве, называется размерностью пространства. Мы живём в трехмерном пространстве, следовательно для задания в нем положения точки нужны три числа. Задание, например, расстояний до трёх опорных точек задает координату в пространстве. Можно за три точки жестко закрепить декартову систему координат, тогда положение точки будет характеризоваться тремя числами (x,y,z).

Экспериментальная геометрия В 19 веке Гаусс и Лобачевский усомнились в справедливости постулатов Евклида превратив геометрию из аксиоматической в экспериментальную науку.

Свойства Времени Во всем пространстве можно ввести единое время, текущее равномерно и одинаково

Эталоны времени и длины Секунда – 1/86164 доля земных суток. Длина – изначально одна сорокамиллионная парижского меридиана. В настоящее время- длина пути, которую свет проходит за 1/2999792458 сек.

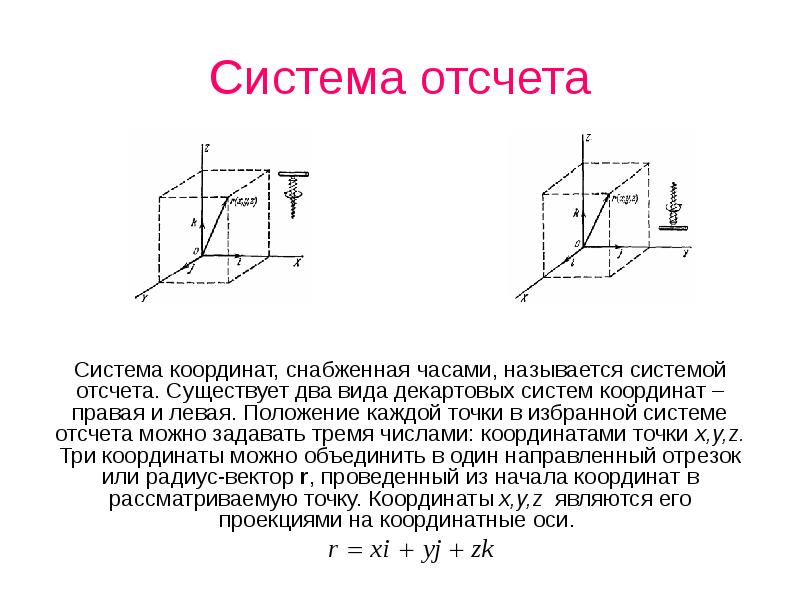
Система отсчета Система координат, снабженная часами, называется системой отсчета. Существует два вида декартовых систем координат – правая и левая. Положение каждой точки в избранной системе отсчета можно задавать тремя числами: координатами точки x,y,z. Три координаты можно объединить в один направленный отрезок или радиус-вектор r, проведенный из начала координат в рассматриваемую точку. Координаты x,y,z являются его проекциями на координатные оси.

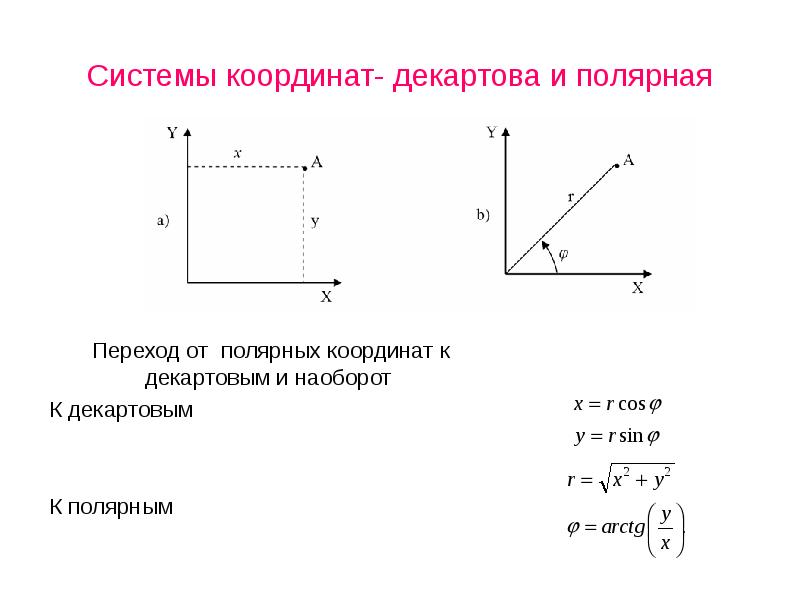
Системы координат- декартова и полярная Переход от полярных координат к декартовым и наоборот К декартовым К полярным

Сферическая система координат Положение точки задается радиусом r , Аксиальным углом , Полярным углом 

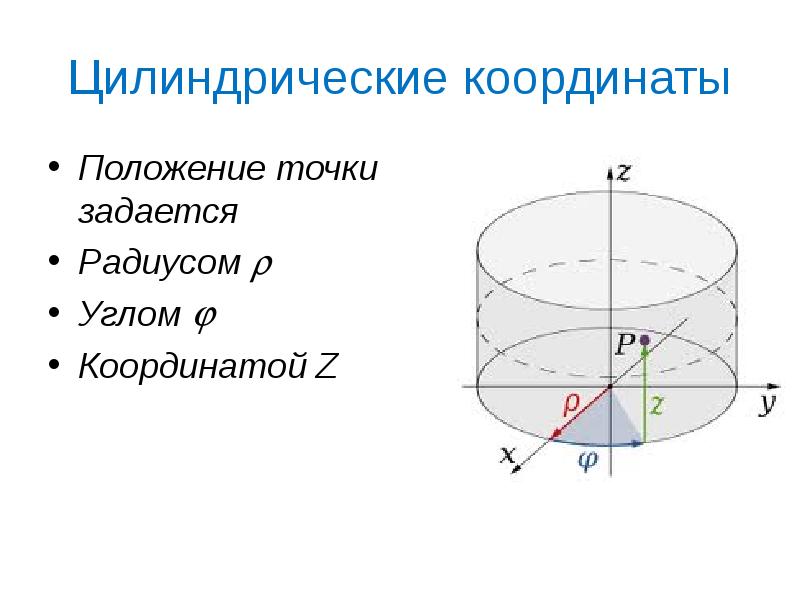
Цилиндрические координаты Положение точки задается Радиусом  Углом  Координатой Z

Скорость и ускорение Средняя скорость за время Δt Мгновенная скорость Ускорение

Примеры расчета скорости и ускорения

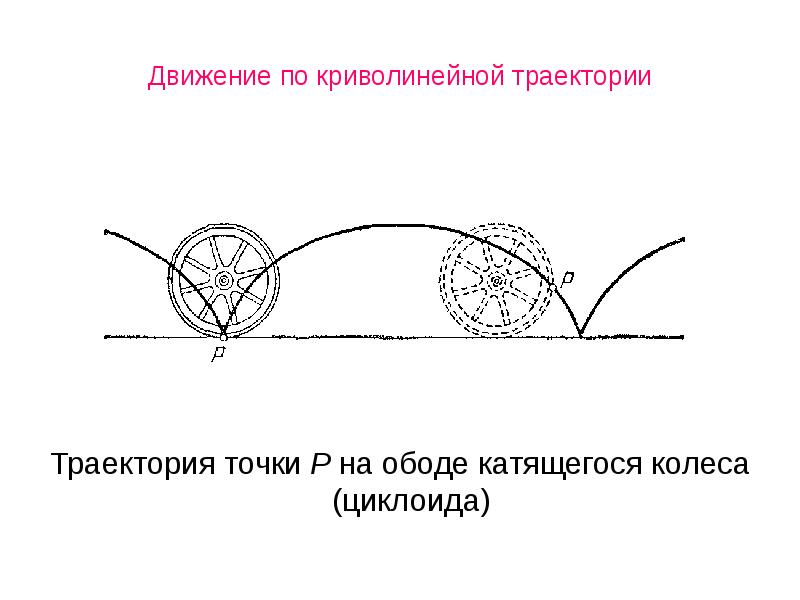
Движение по криволинейной траектории Траекторией Материальной точки называется линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчета.

Движение по криволинейной траектории Траектория точки Р на ободе катящегося колеса (циклоида)

Скорость и ускорение при криволинейном движении Средняя скорость Скорость Ускорение

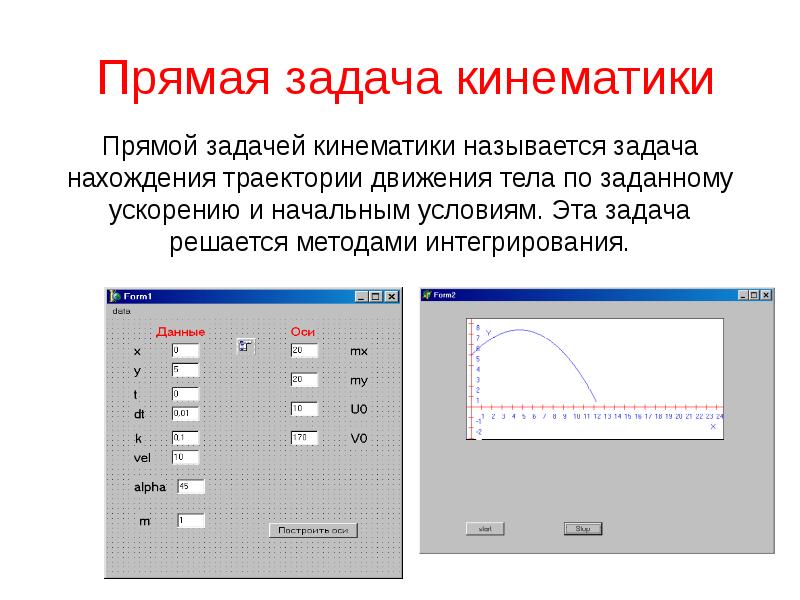
Прямая задача кинематики Прямой задачей кинематики называется задача нахождения траектории движения тела по заданному ускорению и начальным условиям. Эта задача решается методами интегрирования.

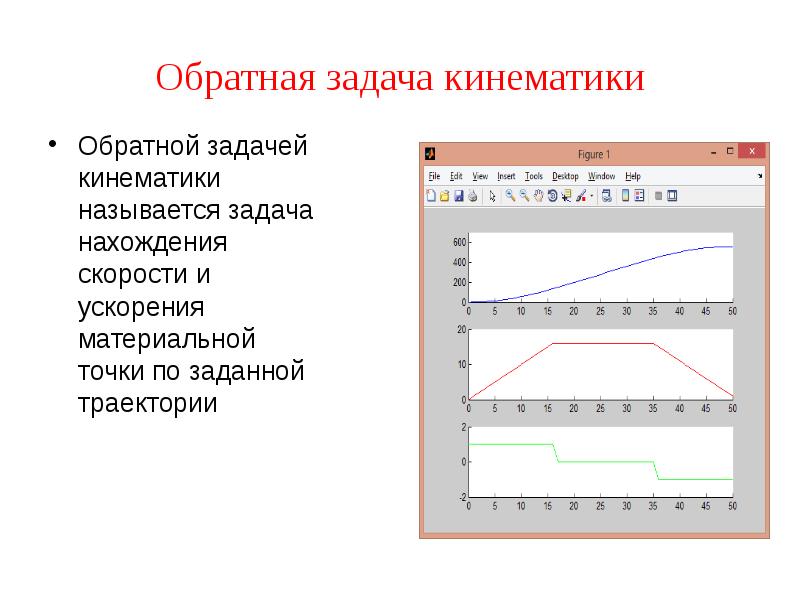
Обратная задача кинематики Обратной задачей кинематики называется задача нахождения скорости и ускорения материальной точки по заданной траектории

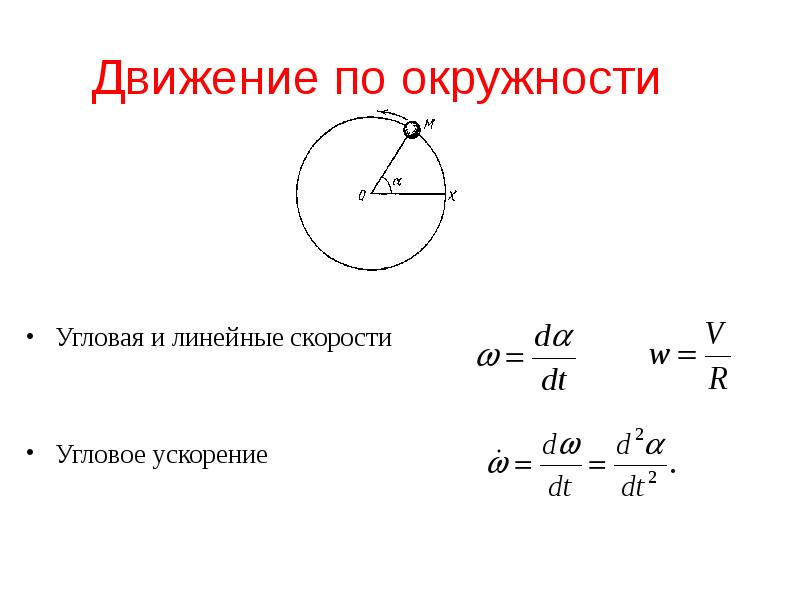
Движение по окружности Угловая и линейные скорости Угловое ускорение

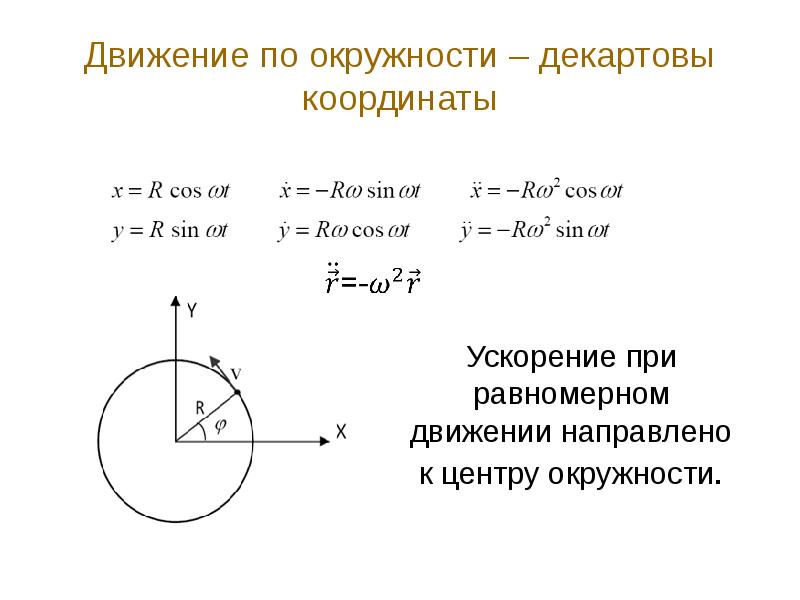
Движение по окружности – декартовы координаты Ускорение при равномерном движении направлено к центру окружности.

Движение по окружности – полярные координаты

Тангенциальное и нормальное ускорения при движении по окружности

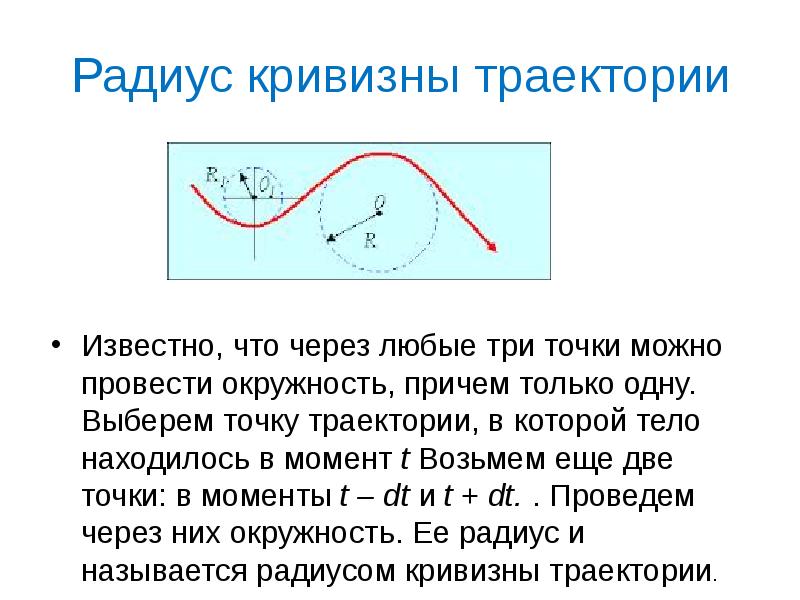
Радиус кривизны траектории Известно, что через любые три точки можно провести окружность, причем только одну. Выберем точку траектории, в которой тело находилось в момент t Возьмем еще две точки: в моменты t – dt и t + dt. . Проведем через них окружность. Ее радиус и называется радиусом кривизны траектории.

Радиус кривизны траектории

Радиус кривизны траектории

Пример: тело брошенное горизонтально

Пример: тело брошенное горизонтально

До встречи через неделю! Республика Алтай. Катунь. Ильгуменский порог.