Закон Ома для участка цепи. (Лекция 11) презентация
Содержание
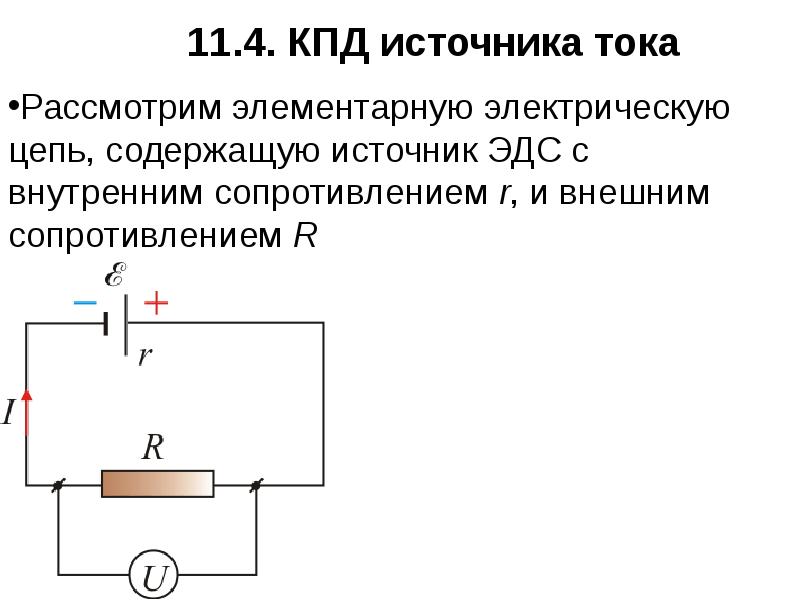
- 2. 11.1. Закон Ома для неоднородного участка цепи Один из
- 3. Георг Симон Ом (1787 – 1854) – немецкий физик. Георг
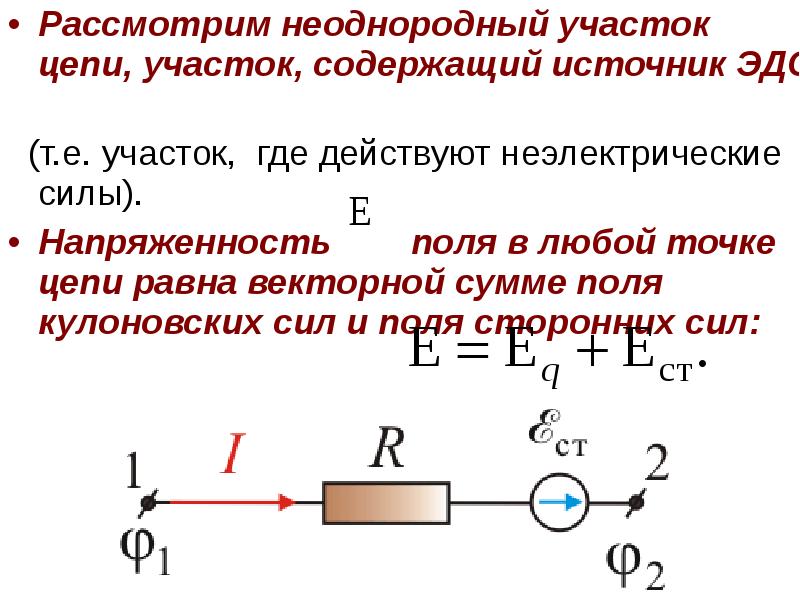
- 4. Рассмотрим неоднородный участок цепи, участок, содержащий источник ЭДС Рассмотрим неоднородный
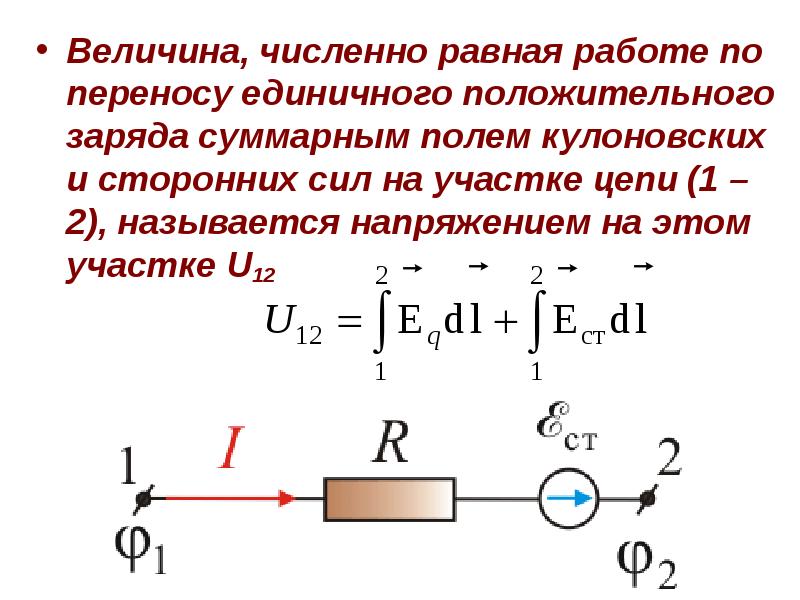
- 5. Величина, численно равная работе по переносу единичного положительного заряда суммарным полем
- 6. т.к. , или
- 7. Напряжение на концах участка цепи совпадает с разностью потенциалов только в
- 8. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи
- 9. В электротехнике часто используют термин падение напряжения – изменение напряжения вследствие
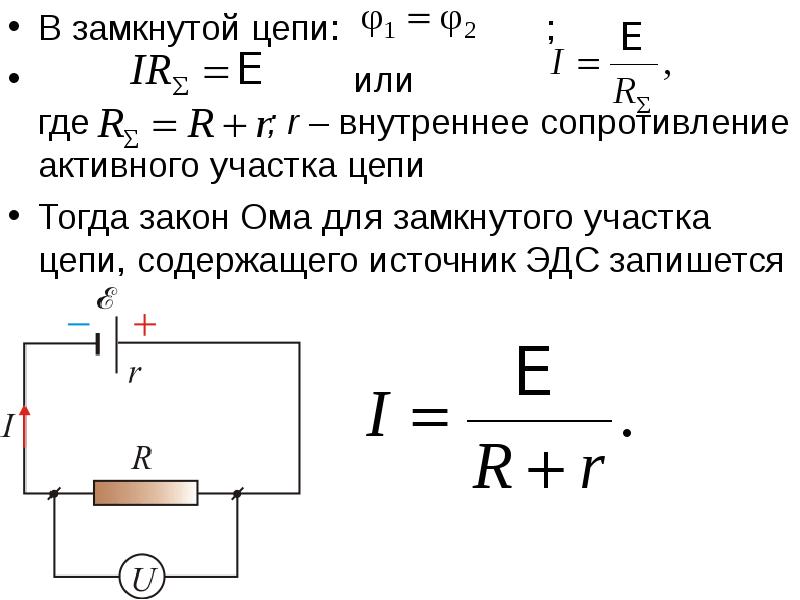
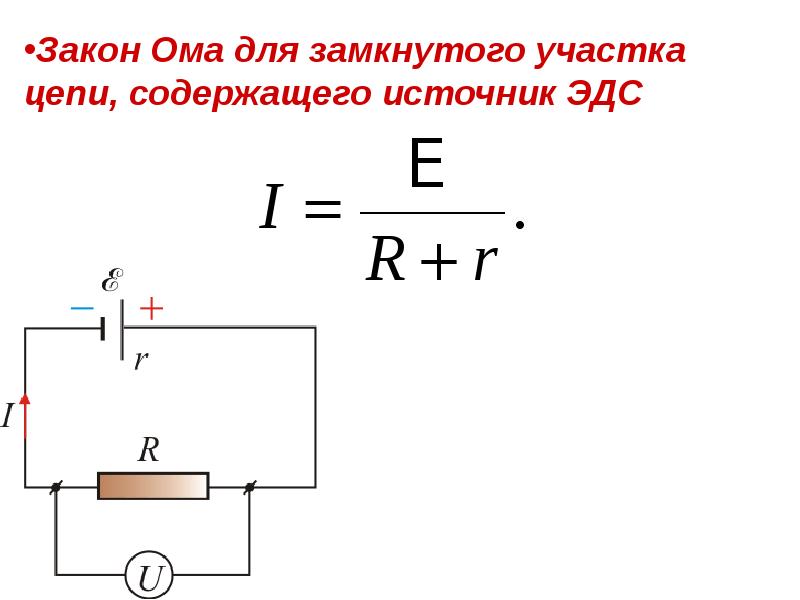
- 10. В замкнутой цепи: ; В замкнутой
- 12. 11.2. Закон Ома в дифференциальной форме Закон Ома в интегральной
- 13. Найдем связь между и в бесконечно малом объеме проводника
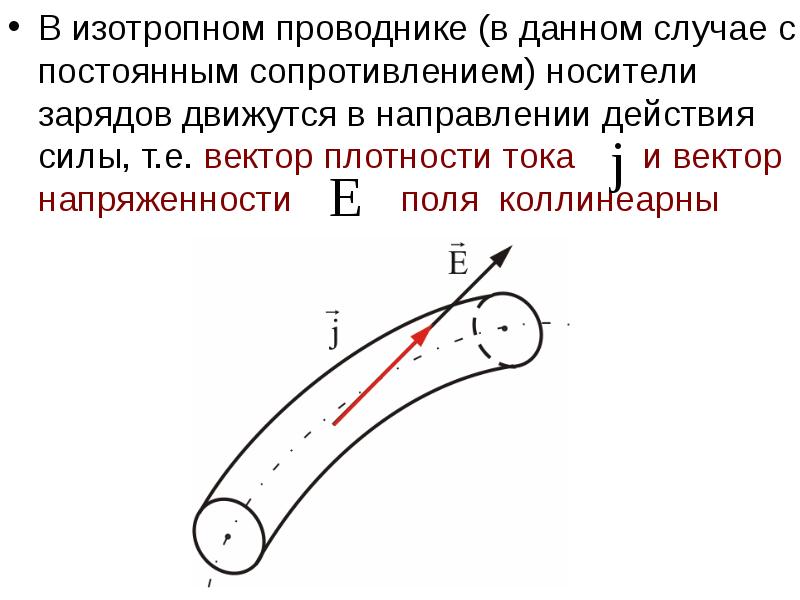
- 14. В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов
- 15. Исходя из закона Ома (11.2.1), имеем: Исходя из закона Ома (11.2.1),
- 16. Плотность тока можно выразить через заряд электрона е, количество зарядов n
- 17. Теперь, если удельную электропроводность σ выразить через е, n и b:
- 18. 11.3. Работа и мощность тока. Закон Джоуля – Ленца Рассмотрим
- 19. Разделив работу на время, получим выражение для мощности: Разделив работу на
- 20. Джоуль Джеймс Пресскотт (1818 – 1889) – английский физик, один из
- 21. При протекании тока, в проводнике выделяется количество теплоты: При протекании тока,
- 22. Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля
- 23. Тепловая мощность тока в элементе проводника Δl, сечением ΔS, объемом
- 24. Согласно закону Ома в дифференциальной форме
- 25. Мощность, выделенная в единице объема проводника . Мощность, выделенная в единице
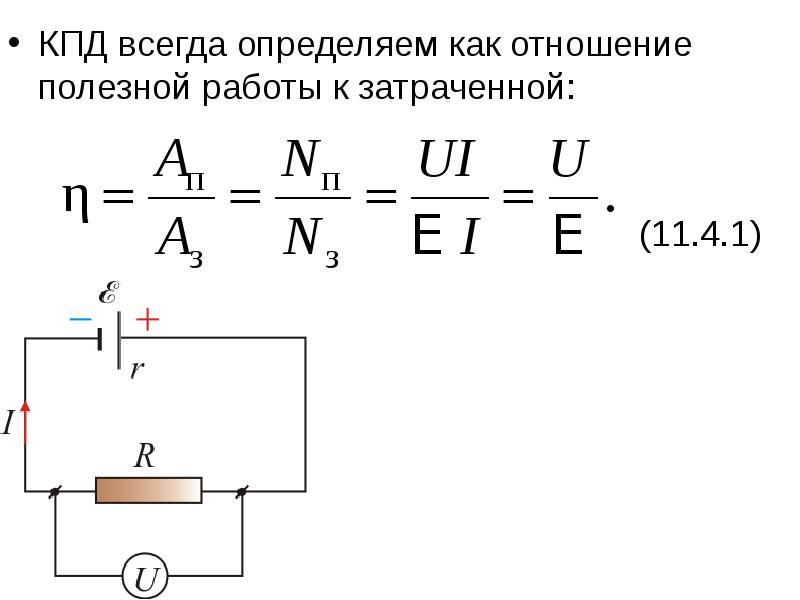
- 27. КПД всегда определяем как отношение полезной работы к затраченной: КПД всегда
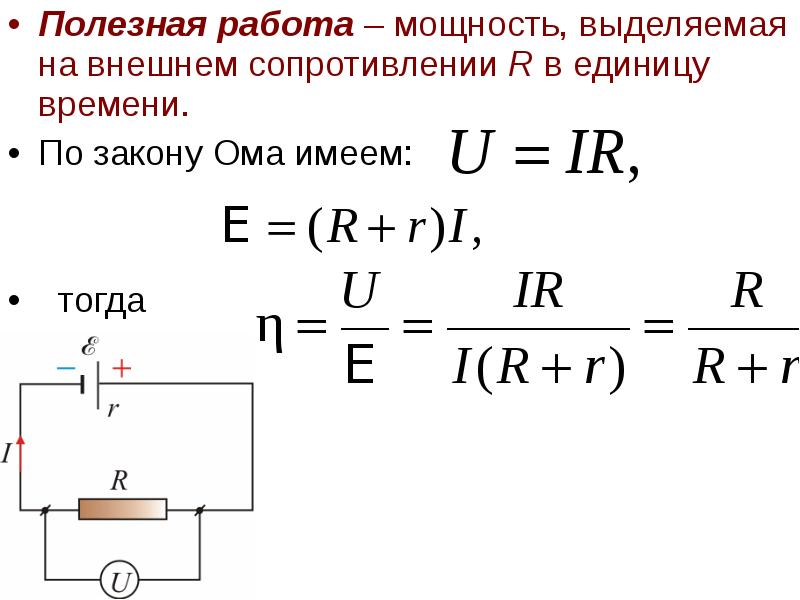
- 28. Полезная работа – мощность, выделяемая на внешнем сопротивлении R в единицу
- 29. Таким образом, имеем, что при Таким образом, имеем, что при
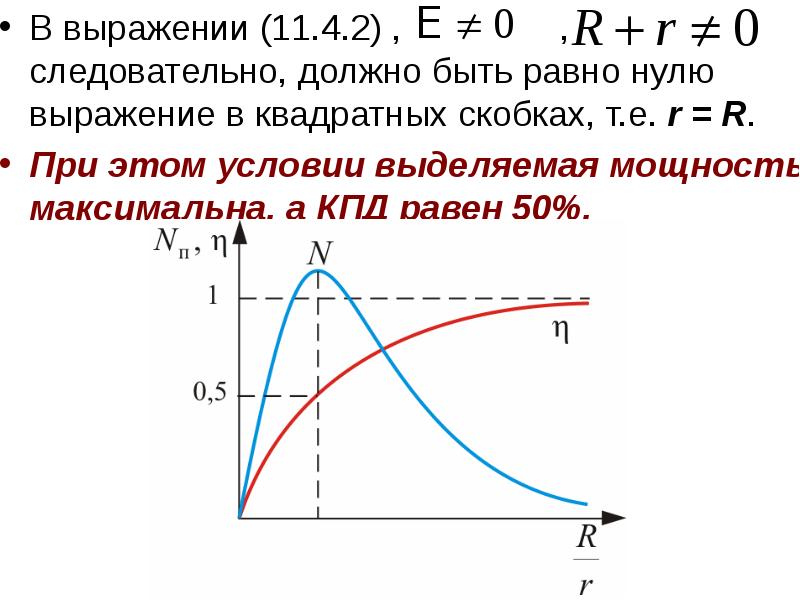
- 30. Это возможно при R = r
- 31. В выражении (11.4.2) , , следовательно, должно быть
- 32. 11.5. Правила Кирхгофа для разветвленных цепей Расчет разветвленных цепей с
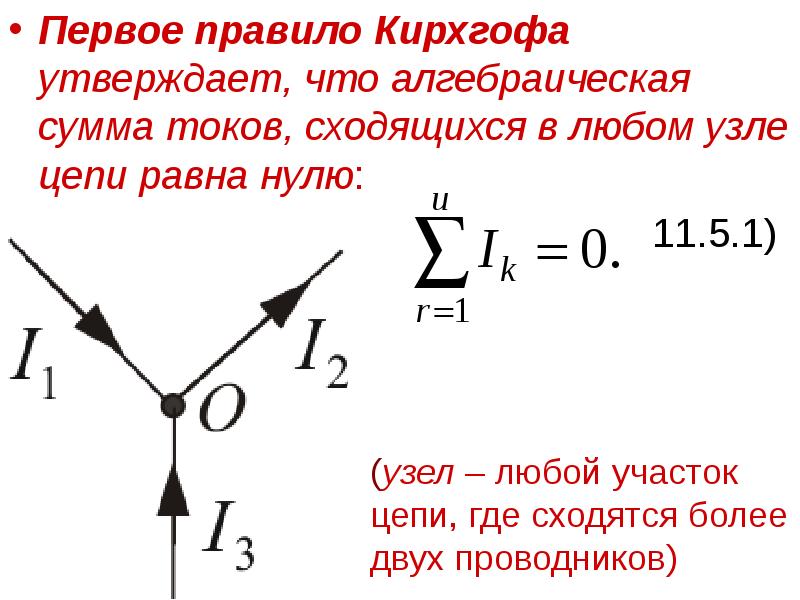
- 33. Первое правило Кирхгофа утверждает, что алгебраическая сумма токов, сходящихся в любом
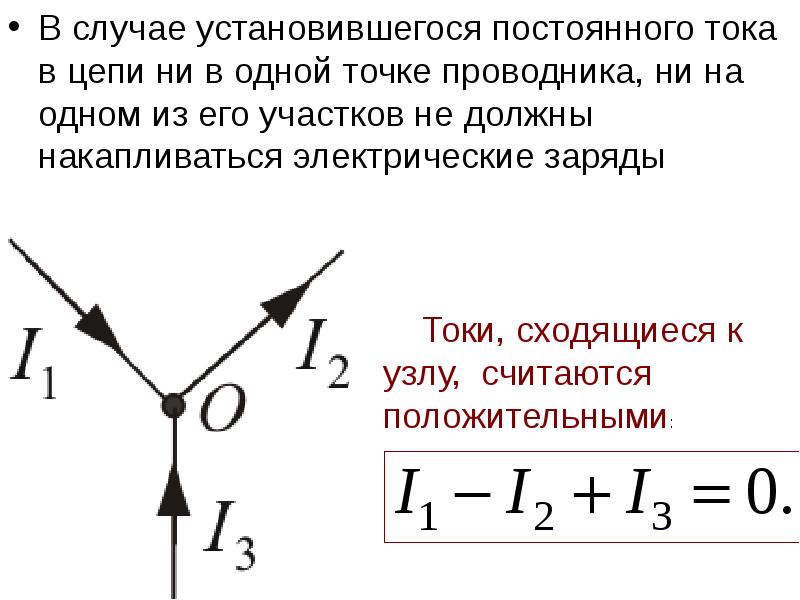
- 34. В случае установившегося постоянного тока в цепи ни в одной точке
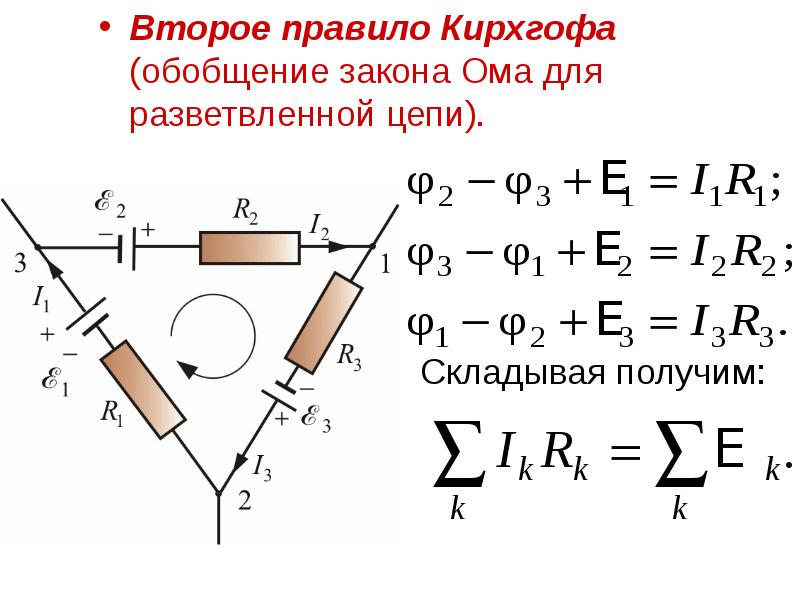
- 35. Второе правило Кирхгофа (обобщение закона Ома для разветвленной цепи). Второе правило
- 36. В любом замкнутом контуре электрической цепи алгебраическая сумма произведения тока на
- 37. ВОТ И ЛЕКЦИИ КОНЕЦ, ВОТ И ЛЕКЦИИ КОНЕЦ, А
- 38. Скачать презентацию



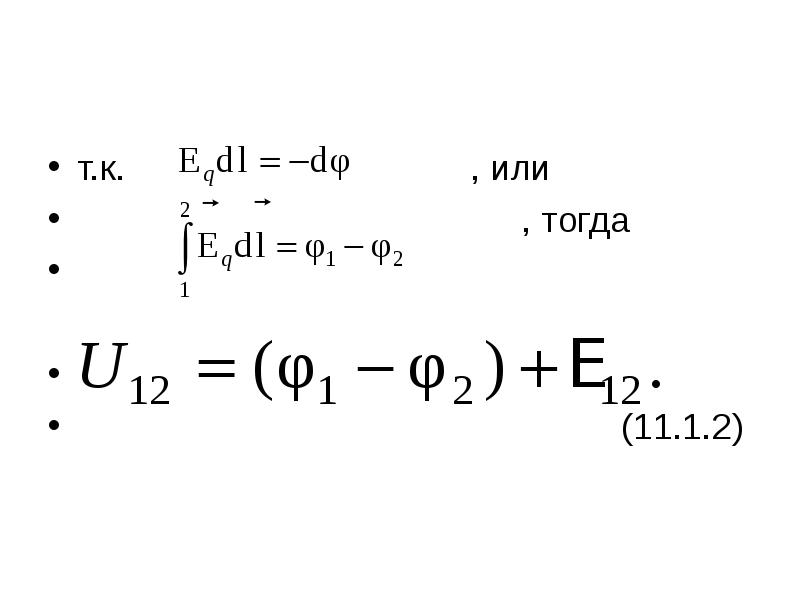





















Слайды и текст этой презентации
Скачать презентацию на тему Закон Ома для участка цепи. (Лекция 11) можно ниже:
Похожие презентации