Тела Архимеда Король А. 10-12 презентация
Содержание
- 2. Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все
- 3. Архимедовы тела названы по имени Архимеда, обсуждавшего их в ныне потерянной работе. Папп ссылается
- 4. Полуправильные многогранники в отличие от правильных (платоновых тел) состоят из двух
- 5. Выпуклый многогранник лежит с одной стороны от плоскости любой из своих
- 6. Усечённый тетраэдр
- 7. Число вершин равно 720°, делённому на дефектe угла вершины. Число вершин равно 720°,
- 8. Различные архимедовы и платоновы тела могут быть получены друг из друга
- 9. Расширение или скашивание осуществляется путём движения граней (в направлении) от центра (на одно
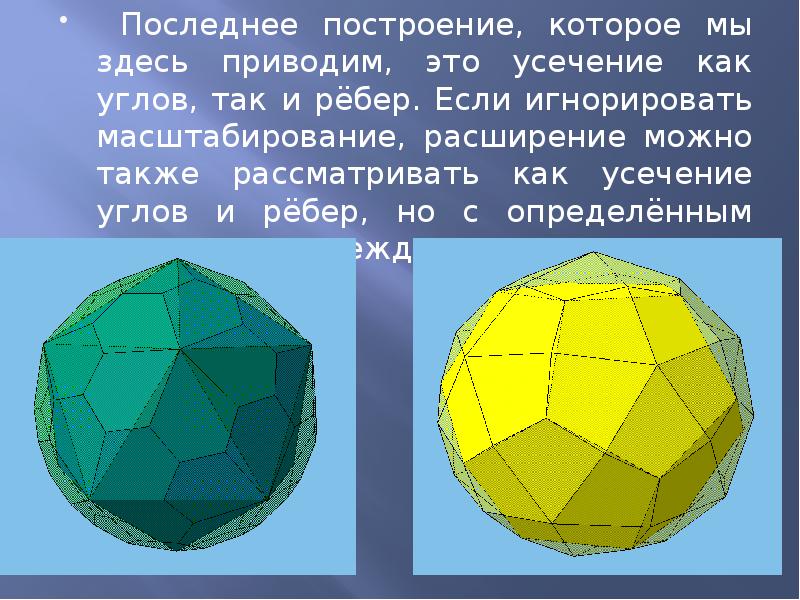
- 10. Последнее построение, которое мы здесь приводим, это усечение как углов, так
- 11. Ссылки на эту работу имеются в трудах математика Паппа. Теорией этих тел
- 13. Скачать презентацию











Слайды и текст этой презентации
Похожие презентации





























