Тема №8 Теория графов презентация

Тема №8 Теория графов Цель темы: рассмотреть основные понятия теории графов; применение графов для формализации задач

Основные понятия Многие задачи сводятся к рассмотрению совокупности объектов, существенные свойства которых описываются связями между ними. НАПРИМЕР – Электрическая схема. - Карта дорог. - Описание конструкции. - Работа цифрового автомата.

Понятие графа В подобных случаях удобно рассматриваемые объекты изображать точками, называемыми вершинами, а связи между ними задавать линиями, называемыми ребрами. Множество вершин V, связи между которыми определены множеством ребер E, называют графом и обозначают G={V;E}

Определения Вершины и рёбра графа называются  элементами графа, число вершин в графе   — порядком, число рёбер   — размером графа. Вершины  U и  V называются концевыми вершинами (или просто концами) ребра e={U,V}  . Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними. Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы совпадают, то есть e={U,U}  .

Типы графов Ориентированный и неориентированный. Смешанный. Конечный и бесконечный. Полный граф. Мультиграф и псевдограф. Двудольный граф или биграф.

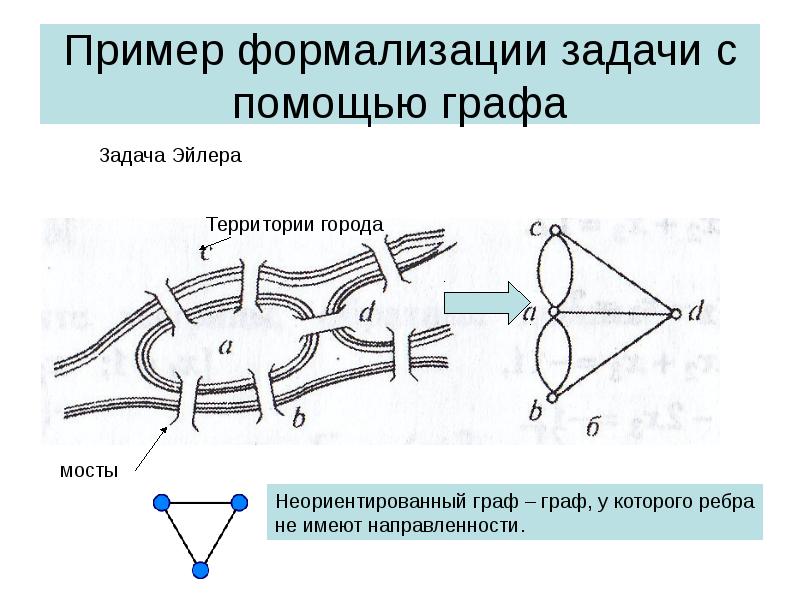
Пример формализации задачи с помощью графа

Ориентированные графы Часто связи между объектами характеризуются определенной ориентацией – направлением. НАПРИМЕР - течение тока, направление передачи сигнала, направление движения автомобилей, причинная связь. Для указания направления ребро графа отмечается стрелкой и называется дугой, а граф с ориентированными ребрами называется орграфом.

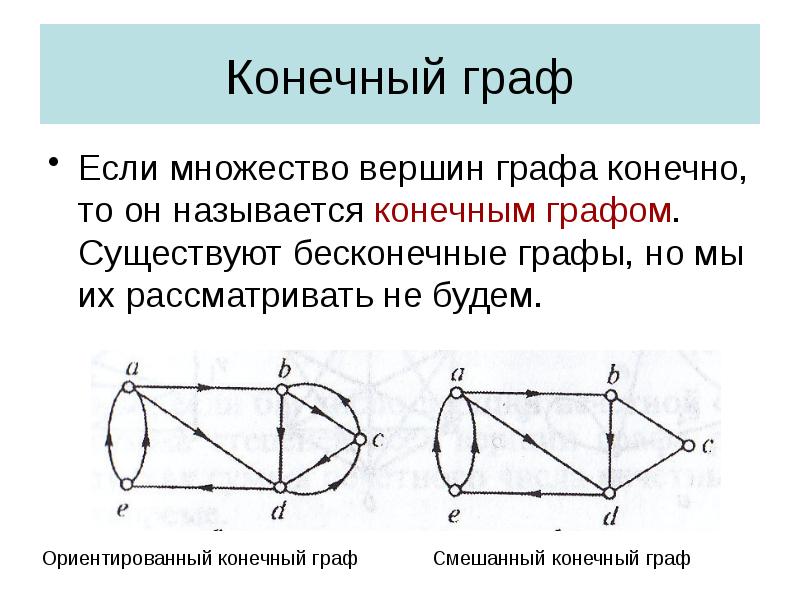
Конечный граф Если множество вершин графа конечно, то он называется конечным графом. Существуют бесконечные графы, но мы их рассматривать не будем.

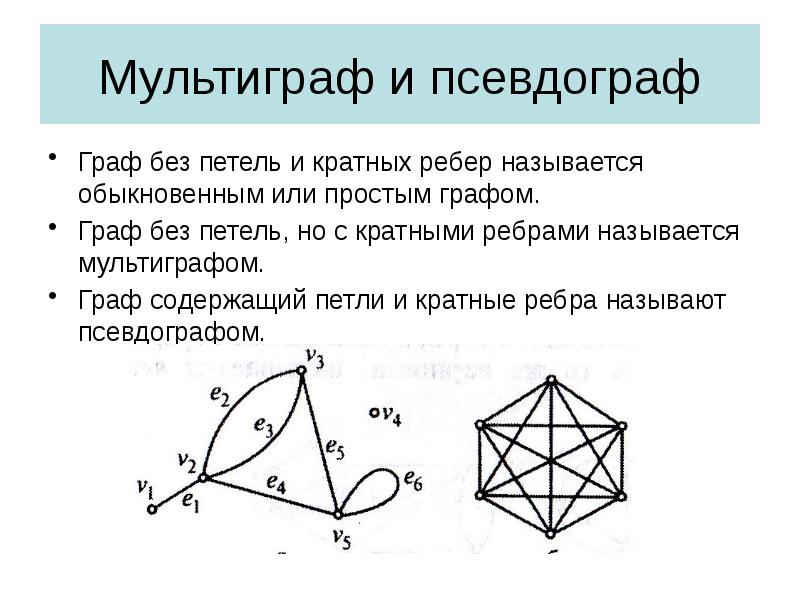
Мультиграф и псевдограф Граф без петель и кратных ребер называется обыкновенным или простым графом. Граф без петель, но с кратными ребрами называется мультиграфом. Граф содержащий петли и кратные ребра называют псевдографом.

Биграф Простой граф, у которого любые две вершины соединены называется полным. Если граф не имеет ребер, то все его вершины изолированы и он называется пустым или нульграфом. Если множество вершин V простого графа допускает такое разбиение на два непересекающихся подмножества V1 и V2, что не существует ребер, соединяющие вершины одного и того же подмножества, то он называется биграфом.

Смежность, инцидентность, степени Две вершины Vi и Vj графа G={V,E} называют смежными. Если они являются вершинами ребра Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин.

Инцидентность, степень Если вершина Vi является началом или концом ребра Ek, то говорят что они инцидентны. Инцидентность определяет отношение разнородных объектов вершин и ребер графа. В орграфах различают положительную и отрицательную инцидентность. Число ребер, инцидентных вершине называют степенью вершины. Петля учитывается дважды.

Теорема 1 Для любого псевдографа сумма степеней всех его вершин – число четное равное удвоенному числу ребер графа. ДОКАЗАТЕЛЬСТВО: Заключение этой теоремы следует из того, что каждое ребро имеет два конца, а каждая петля учитывается два раза. СЛЕДСТВИЕ: В любом конечном графе число вершин нечетной степени четно.

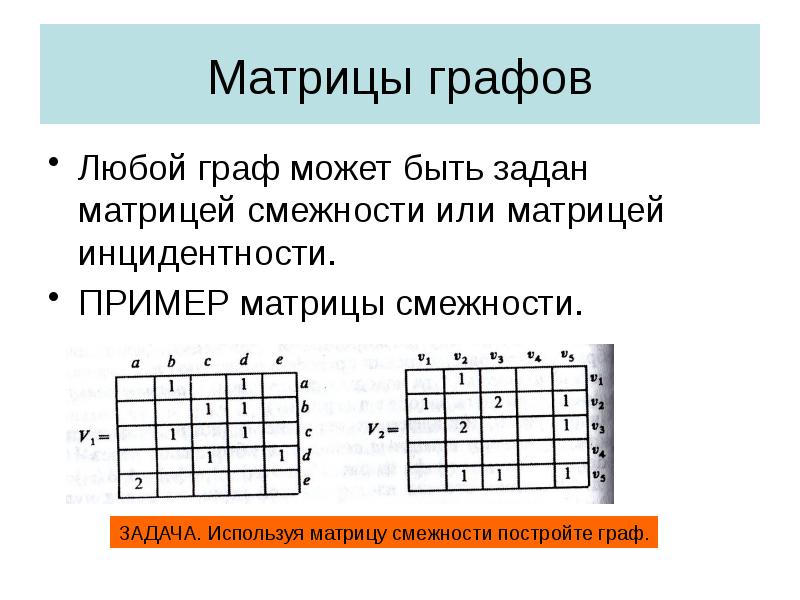
Матрицы графов Любой граф может быть задан матрицей смежности или матрицей инцидентности. ПРИМЕР матрицы смежности.

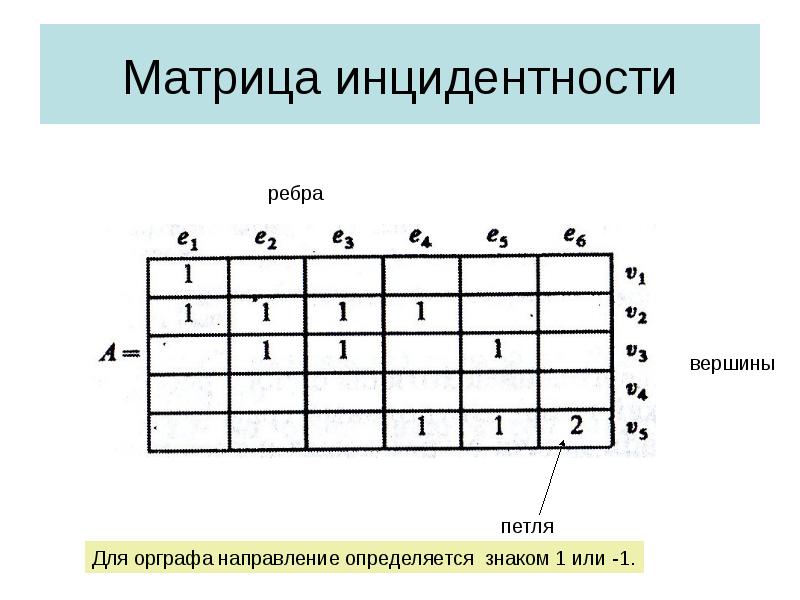
Матрица инцидентности

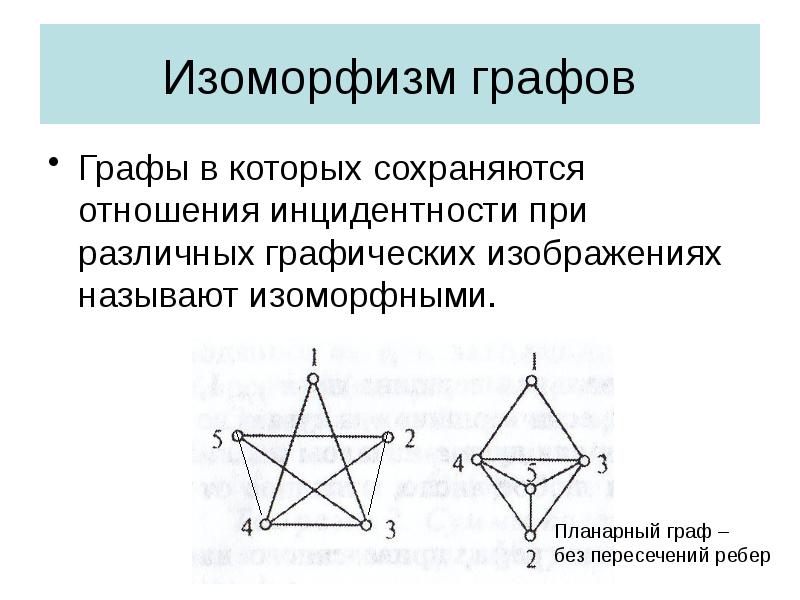
Изоморфизм графов Графы в которых сохраняются отношения инцидентности при различных графических изображениях называют изоморфными.

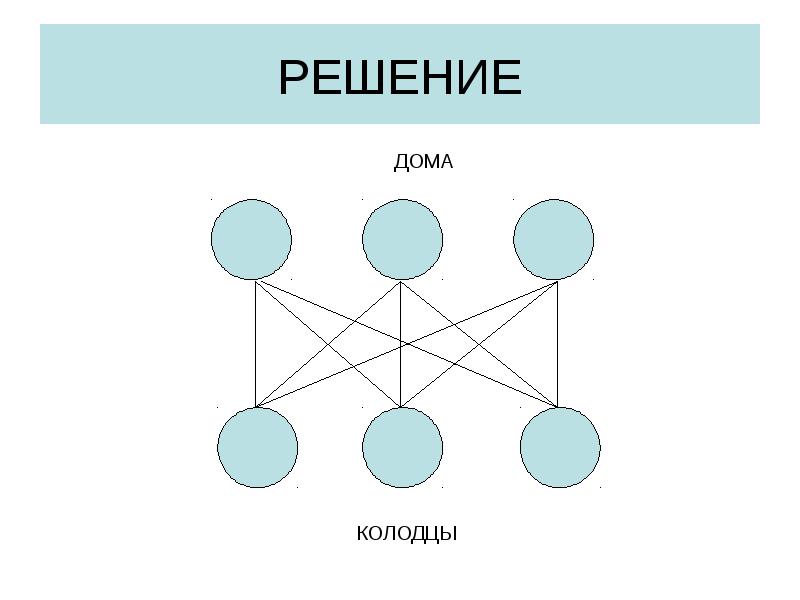
ЗАДАЧА Три дома с враждующими соседями и три колодца. ВОПРОС Можно ли проложить дороги от домов к колодцам так, что бы соседи идя к колодцу не встречались друг с другом?

РЕШЕНИЕ

Особенность планарных графов У планарных графов существует закономерность между количеством вершин В ребер Р и граней Г. В – Р + Г = 2

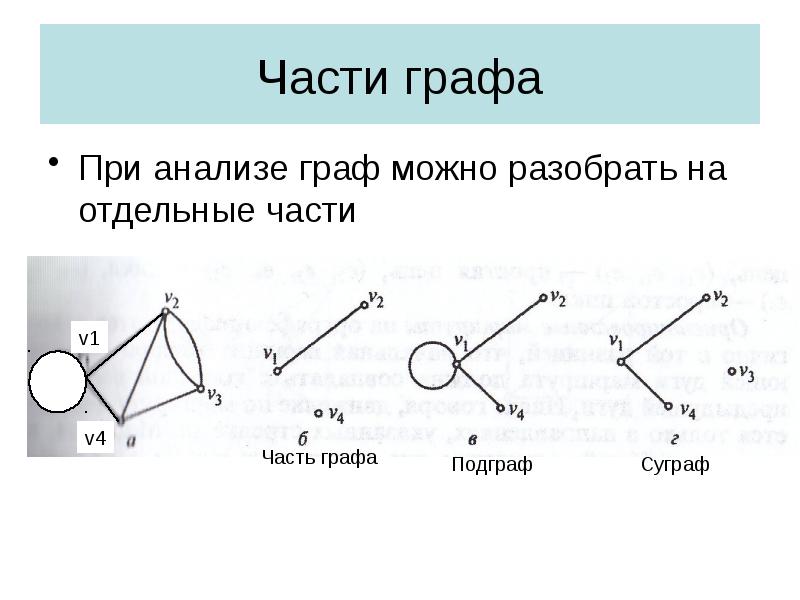
Части графа При анализе граф можно разобрать на отдельные части

Маршруты, цепи, циклы, пути Пусть G неориентированный граф. Маршрутом в G называется такая последовательность ребер, в которой каждые два ребра имеют инцидентную вершину. В маршруте одно и тоже ребро может встречаться несколько раз. В маршруте существует понятие начала и конца маршрута.

Коммутация абонентов через сеть транзитных узлов

Цепь и путь Маршрут, все ребра которого различны называется цепью. Маршрут у которого различны все вершины называется простой цепью. Замкнутая цепь называется циклом. Понятие ориентированный маршрут используется на орграфе. Число ребер маршрута называется длиной пути.

Связность Две вершины графа называются связанными если существует маршрут соединяющий эти вершины. Граф, у которого любая пара вершин связана называется связным графом. В противном случае граф называется несвязным.

Расстояние Расстоянием между вершинами неориентированного связного графа называют минимальную длину простой цепи связывающую эти вершины. Центром графа называется вершина, от которой максимальное расстояние до других вершин являлось бы минимальным. Максимальное расстояние от центра графа до его вершин называется радиусом графа.

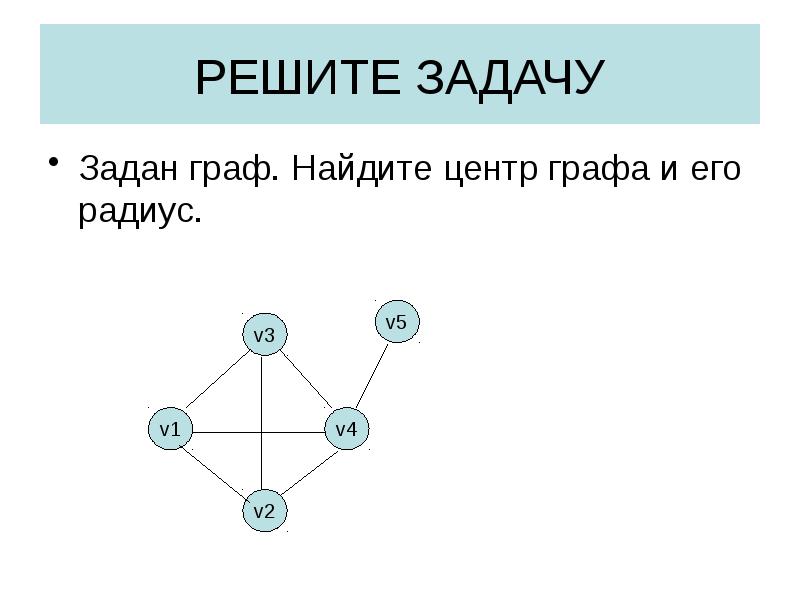
РЕШИТЕ ЗАДАЧУ Задан граф. Найдите центр графа и его радиус.

Эйлеровы циклы и цепи Эйлеров цикл – цикл графа, содержащий все ребра графа. Эйлеров граф - граф, имеющий эйлеров цикл (Эйлеров цикл можно считать следом пера, вычерчивающего граф без отрыва от бумаги). ОПРЕДЕЛИТЕ ЭЛЕРОВ ЦИКЛ НА ГРАФАХ

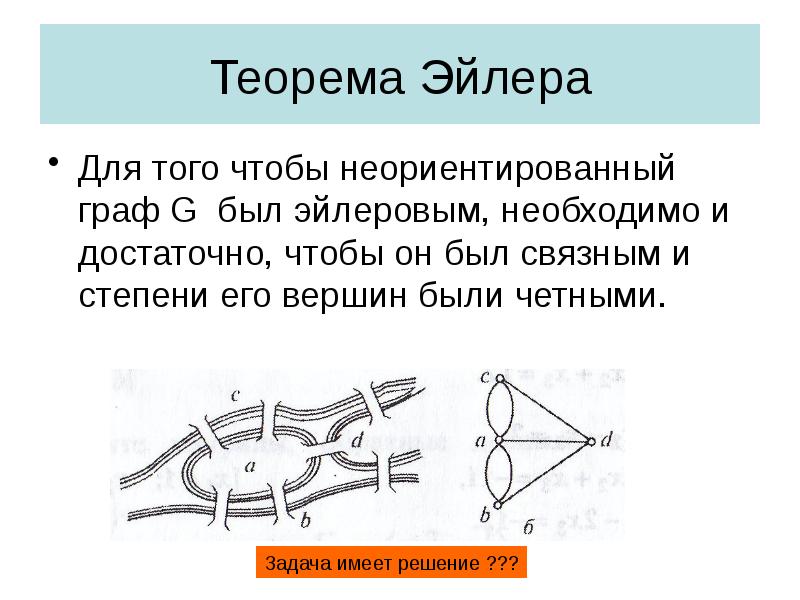
Теорема Эйлера Для того чтобы неориентированный граф G был эйлеровым, необходимо и достаточно, чтобы он был связным и степени его вершин были четными.

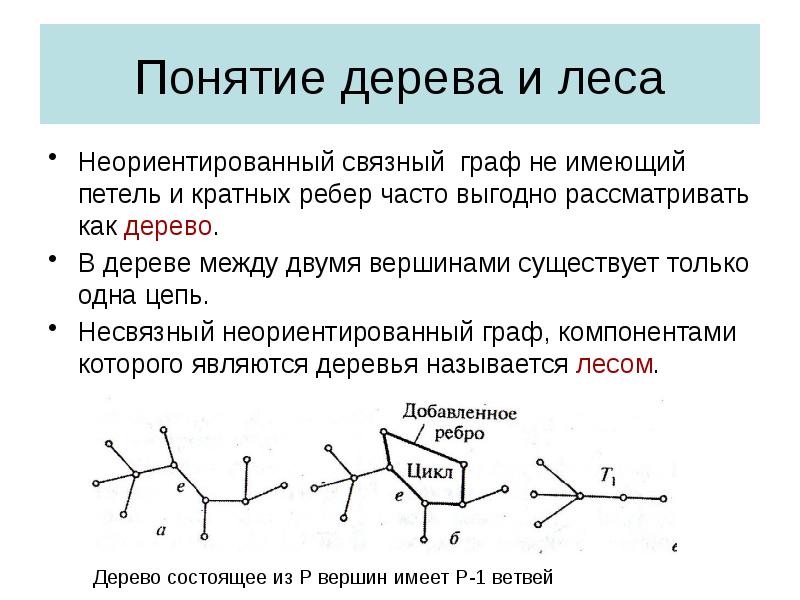
Понятие дерева и леса Неориентированный связный граф не имеющий петель и кратных ребер часто выгодно рассматривать как дерево. В дереве между двумя вершинами существует только одна цепь. Несвязный неориентированный граф, компонентами которого являются деревья называется лесом.

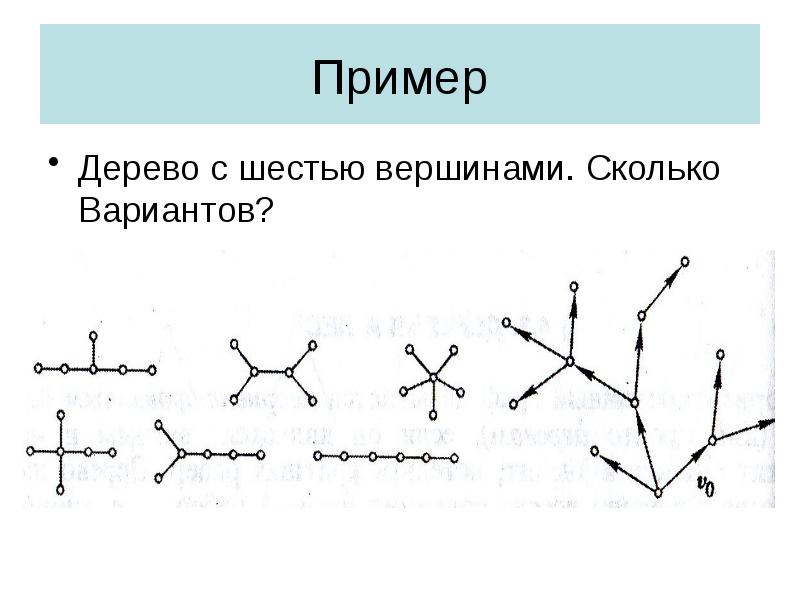
Пример Дерево с шестью вершинами. Сколько Вариантов?

Операции над графами 1. Объединением графов G1(V1, E1) и G2(V2, E2)  называется граф G(V, E) =  , где  V =  , E =  .

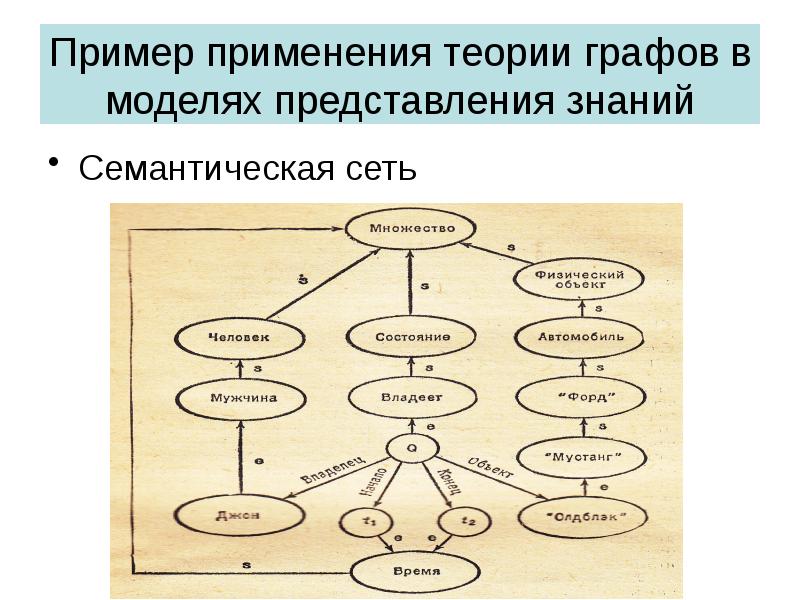
Пример применения теории графов в моделях представления знаний Семантическая сеть

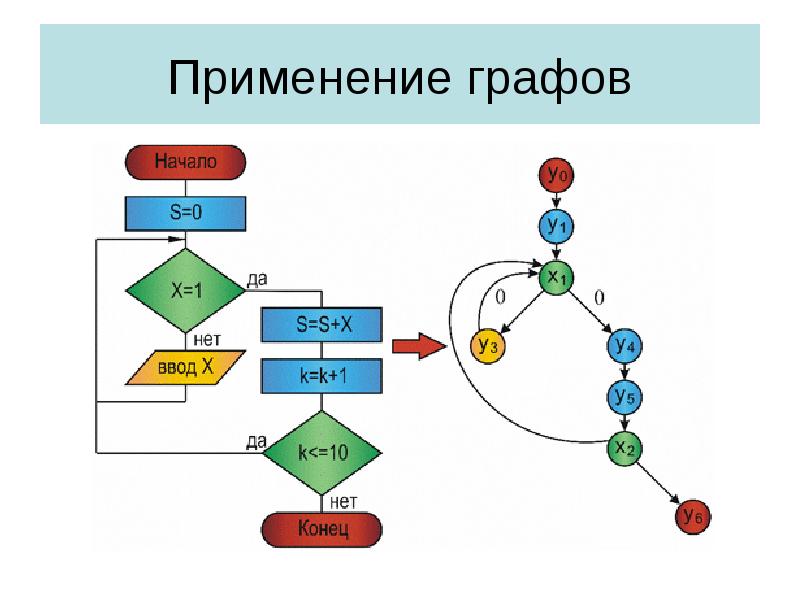
Применение графов

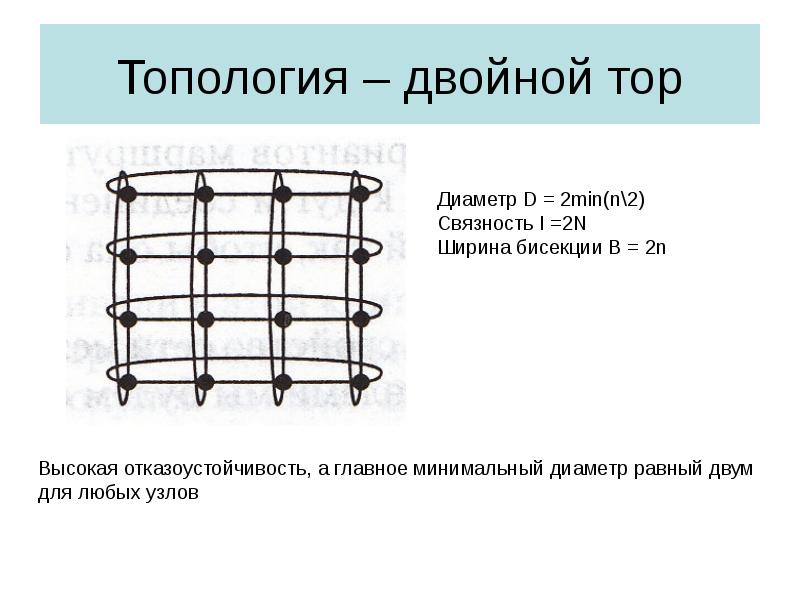
Топология – двойной тор

Области применения теории графов Биология Химия. Экономика. Транспорт. Логистика.