Тема урока: «Сфера и шар.» Цели : ввести понятие сферы, шара и их элементов; презентация
Содержание
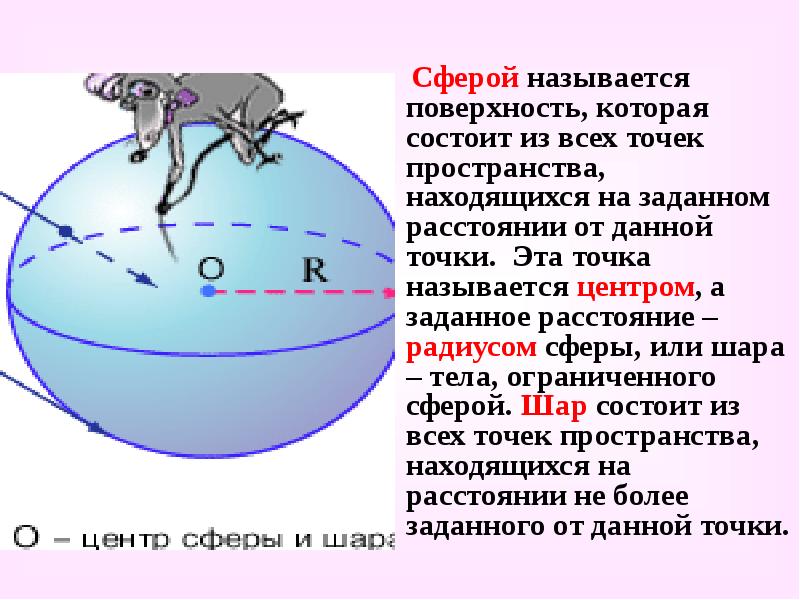
- 2. Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на
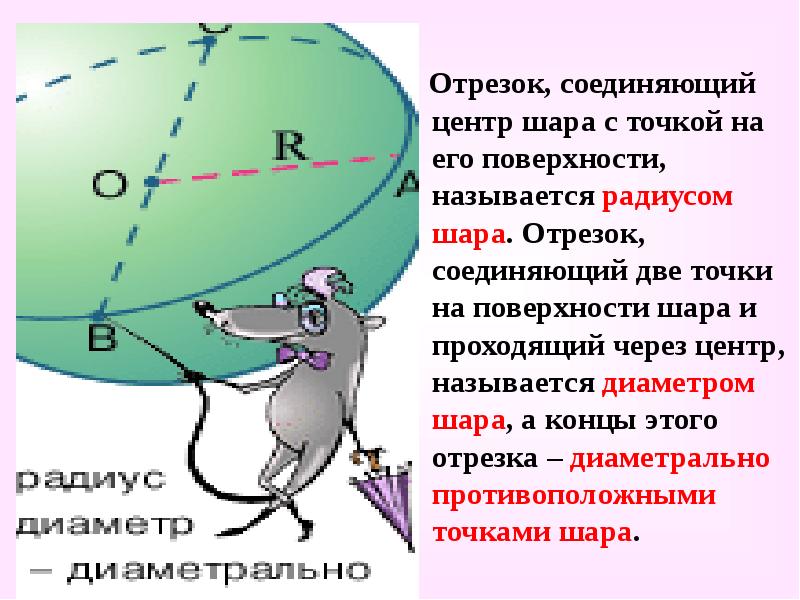
- 3. Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом
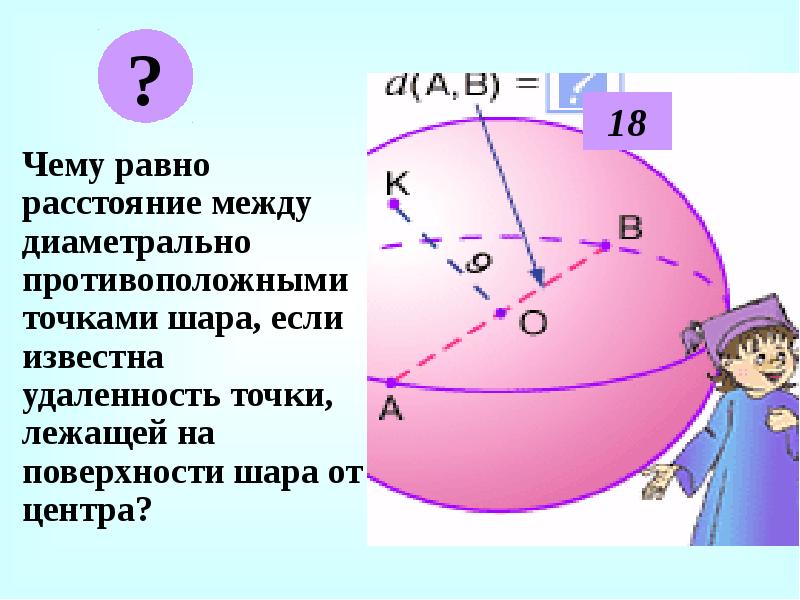
- 4. Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность
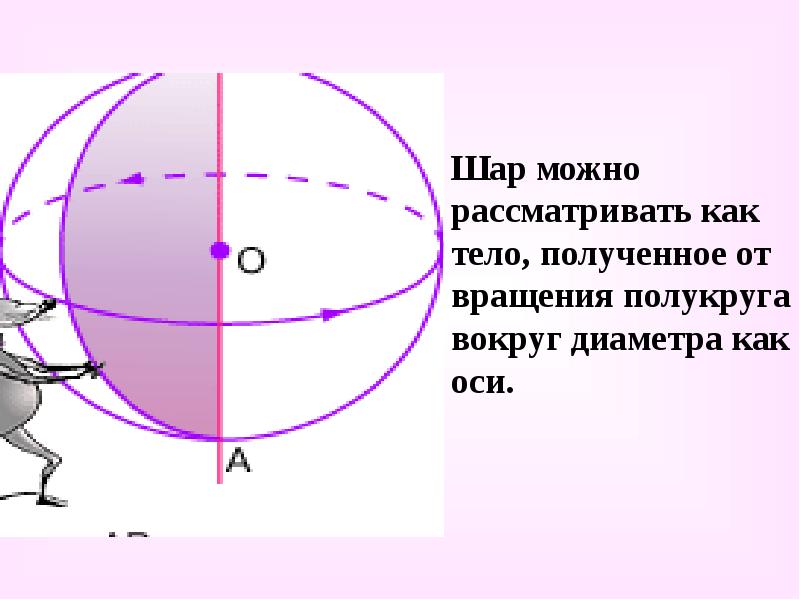
- 5. Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра
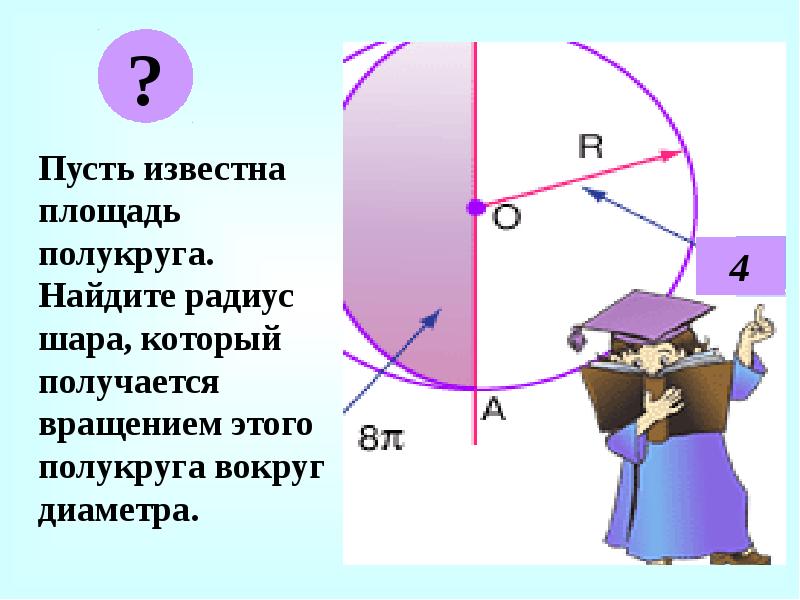
- 6. Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого
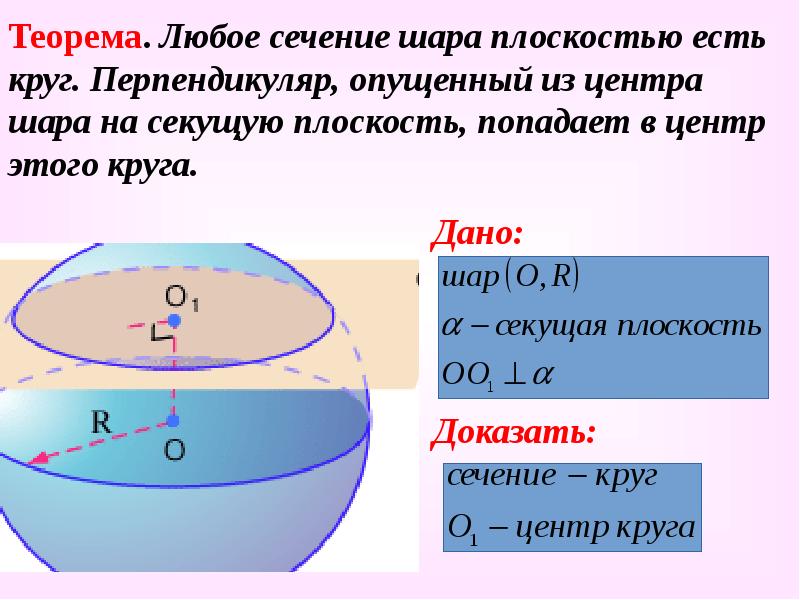
- 7. Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра
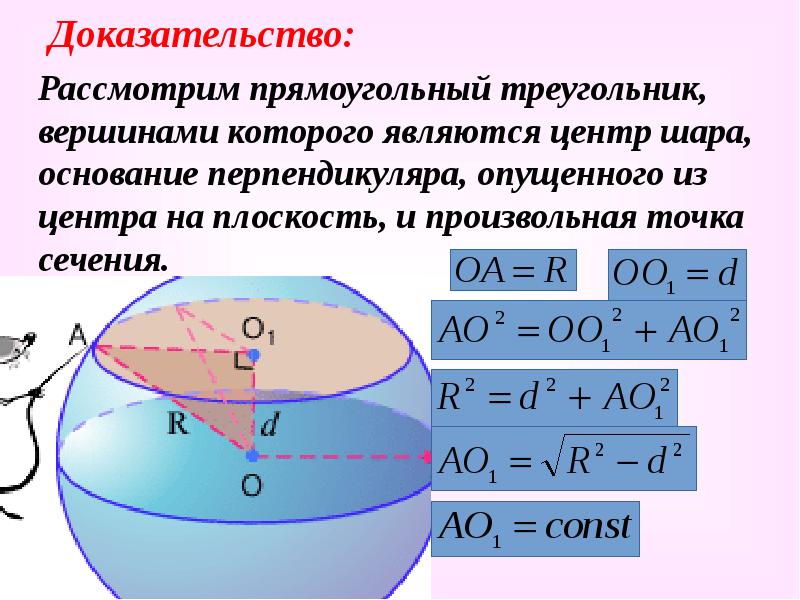
- 8. Доказательство: Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание
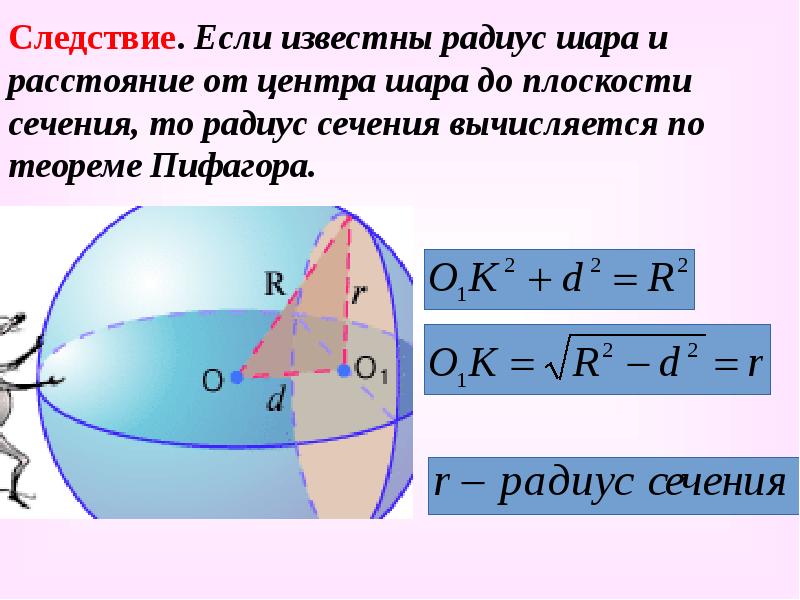
- 9. Следствие. Если известны радиус шара и расстояние от центра шара до
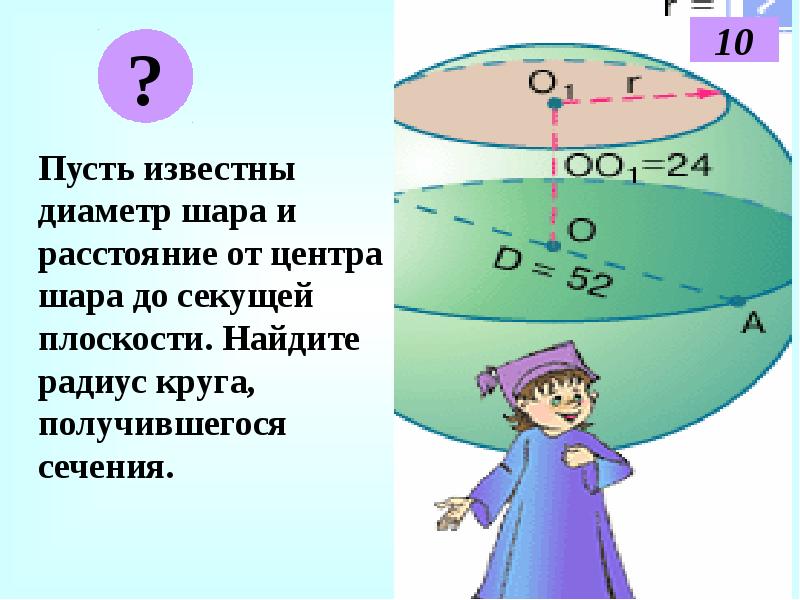
- 10. Пусть известны диаметр шара и расстояние от центра шара до секущей
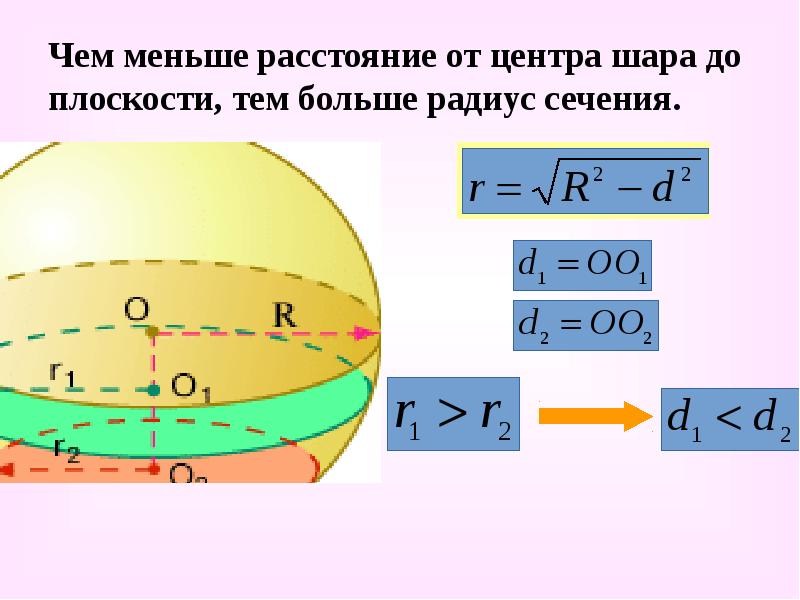
- 11. Чем меньше расстояние от центра шара до плоскости, тем больше радиус
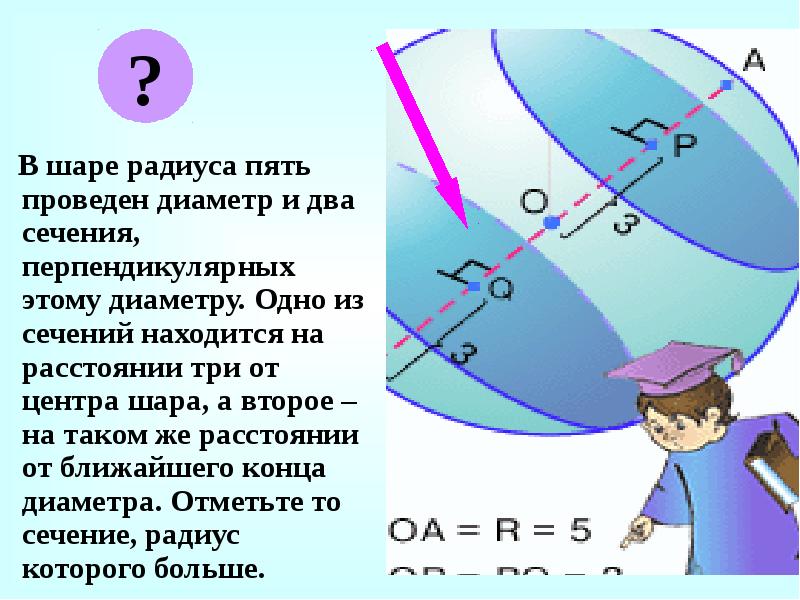
- 12. В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому
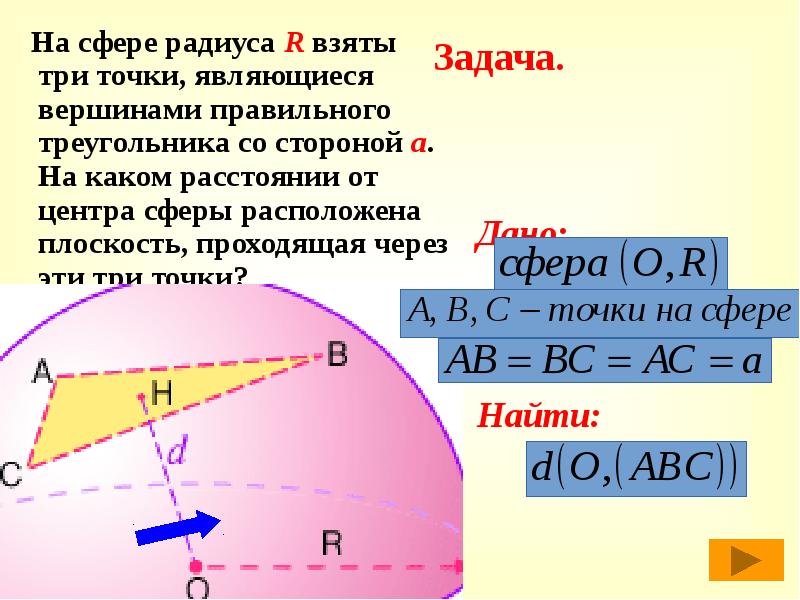
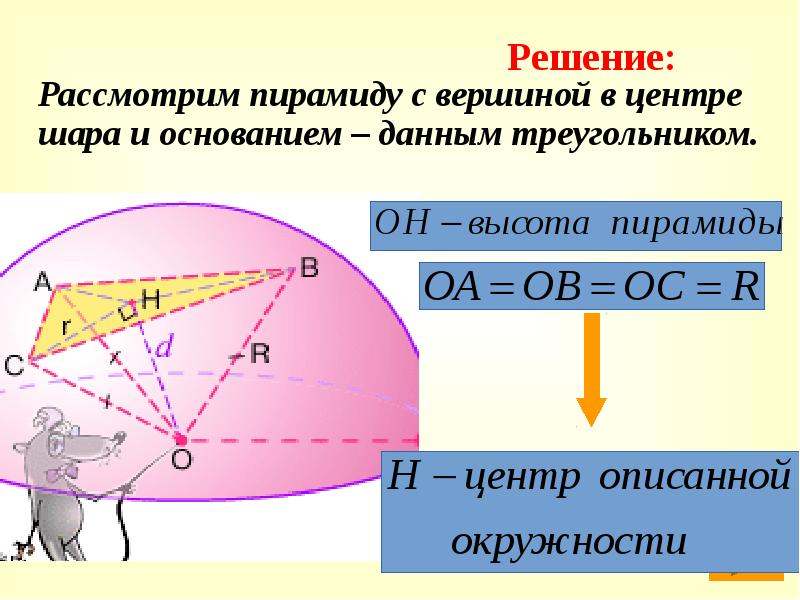
- 13. Задача. На сфере радиуса R взяты три точки, являющиеся вершинами
- 14. Рассмотрим пирамиду с вершиной в центре шара и основанием – данным
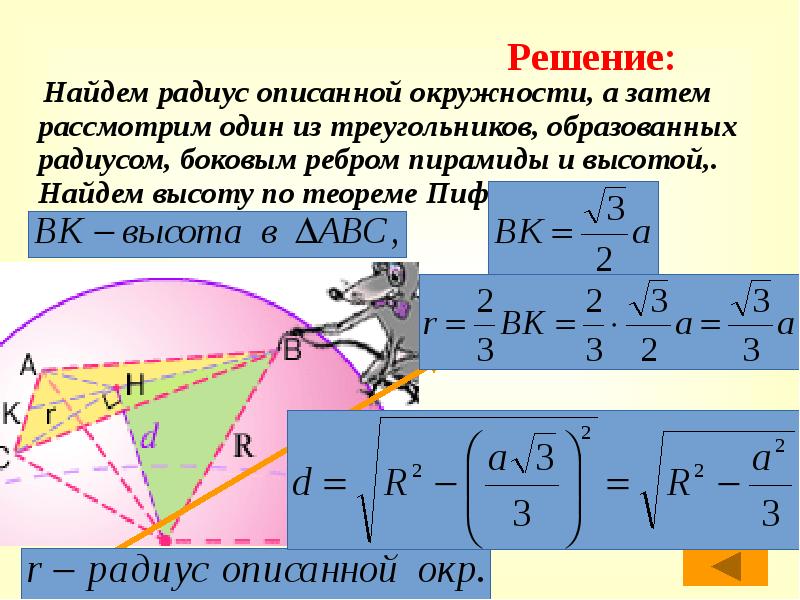
- 15. Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных
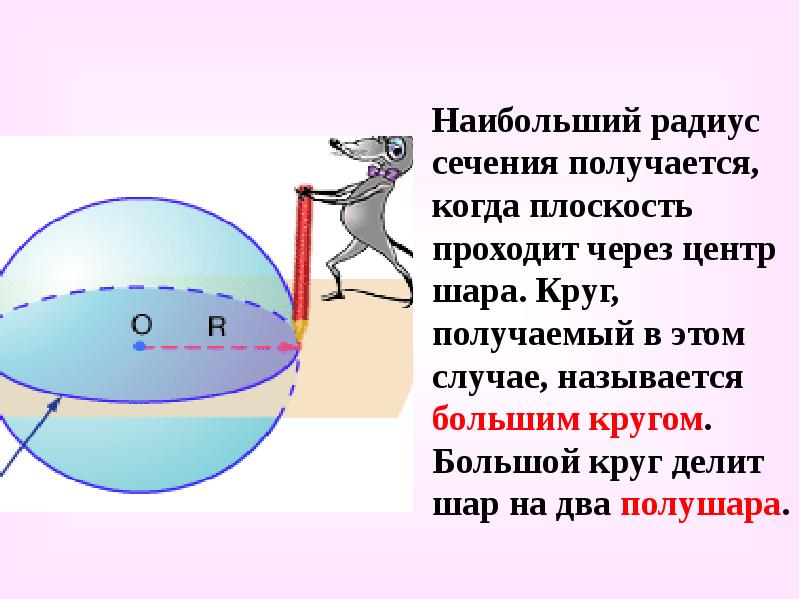
- 16. Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг,
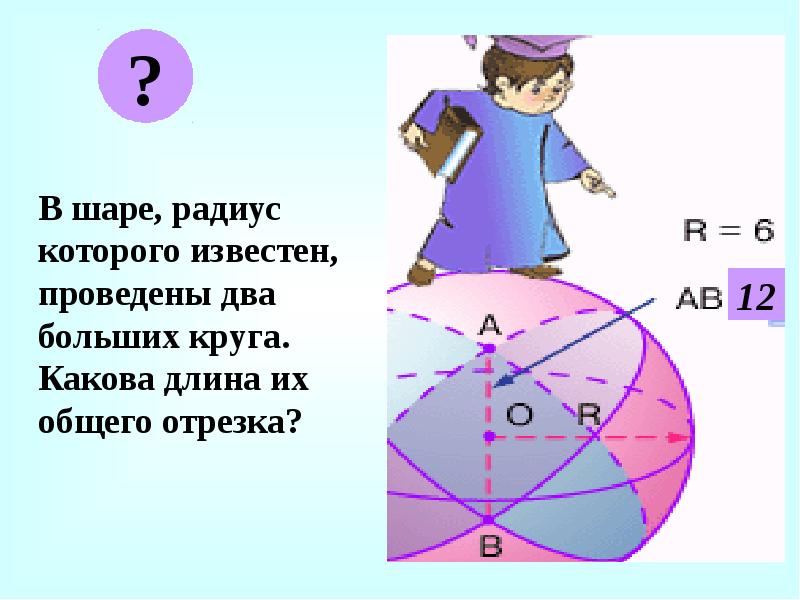
- 17. В шаре, радиус которого известен, проведены два больших круга. Какова длина
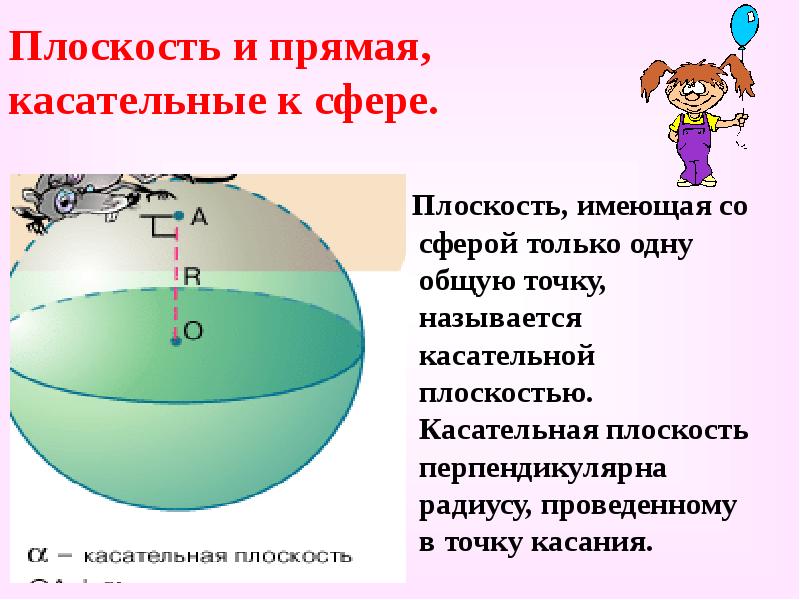
- 18. Плоскость и прямая, касательные к сфере. Плоскость, имеющая со сферой
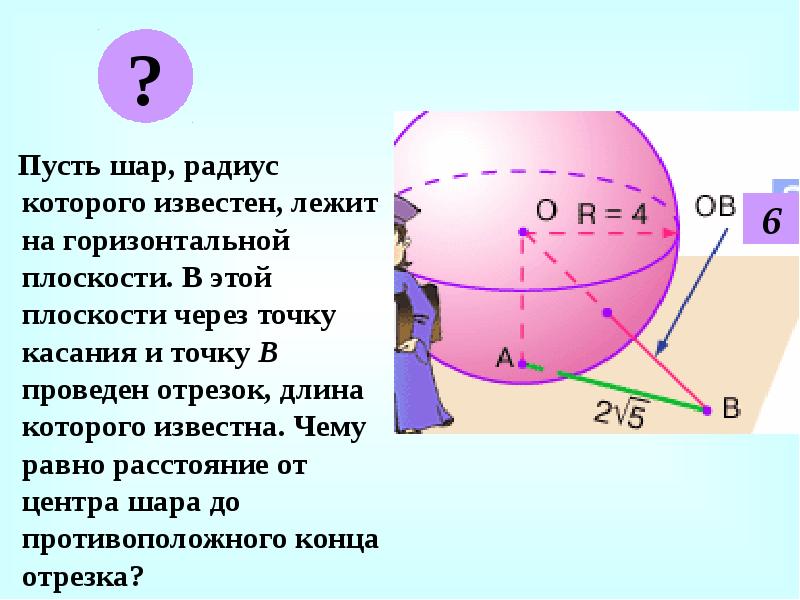
- 19. Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой
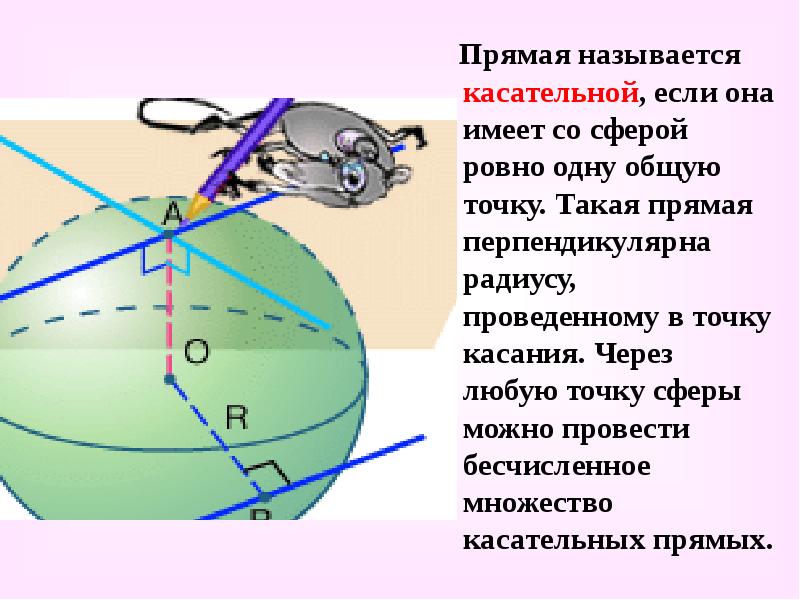
- 20. Прямая называется касательной, если она имеет со сферой ровно одну общую
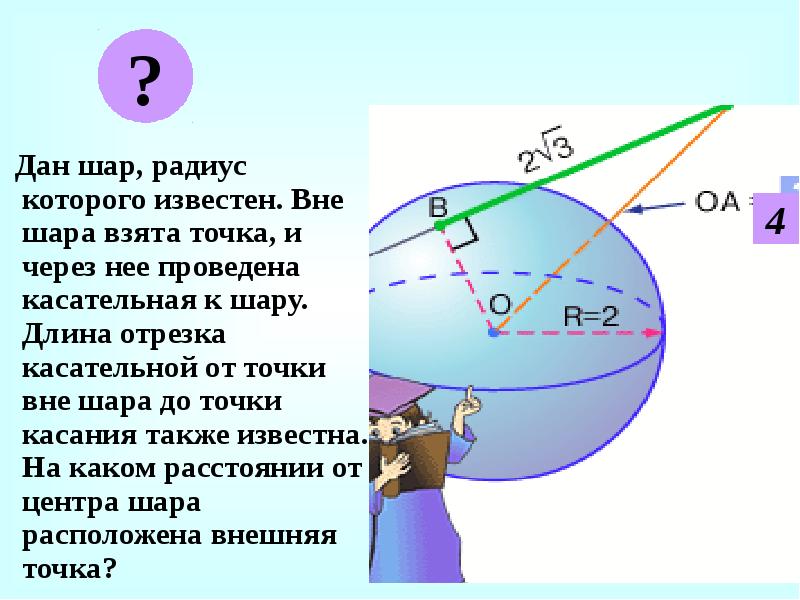
- 21. Дан шар, радиус которого известен. Вне шара взята точка, и через
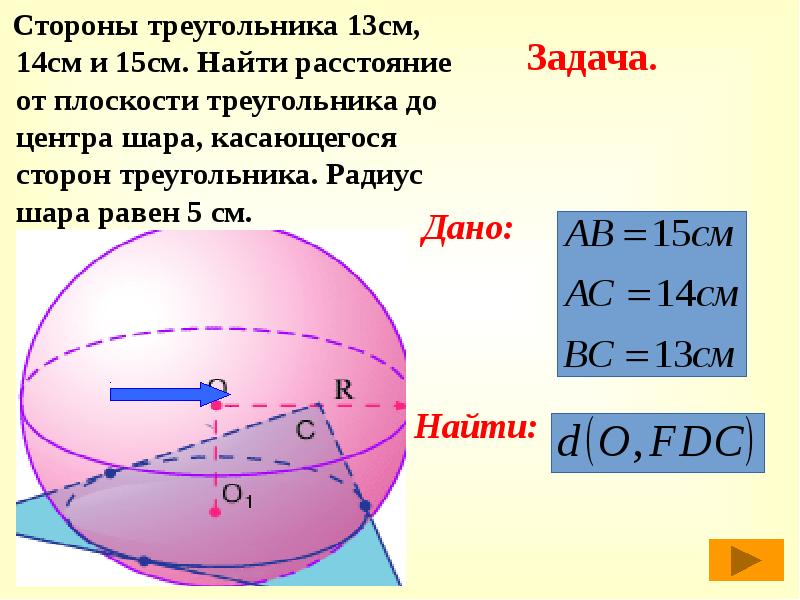
- 22. Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника
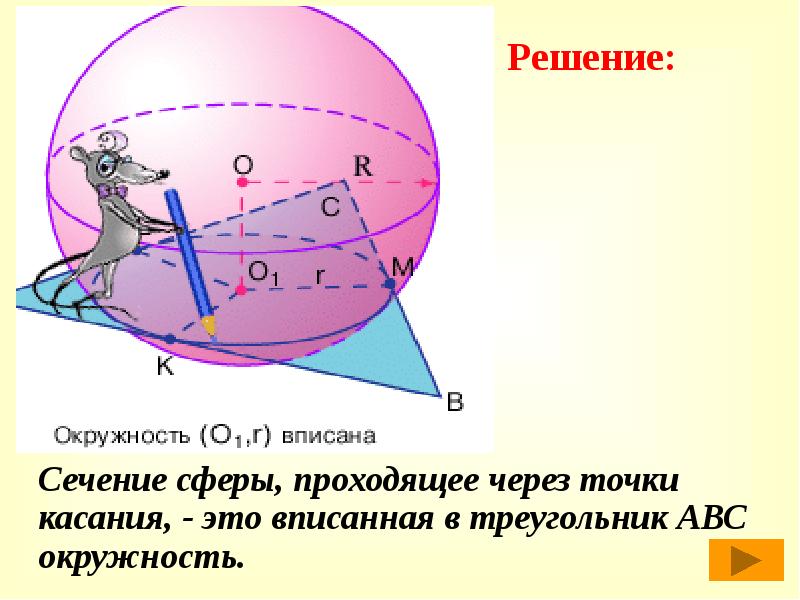
- 23. Сечение сферы, проходящее через точки касания, - это вписанная в треугольник
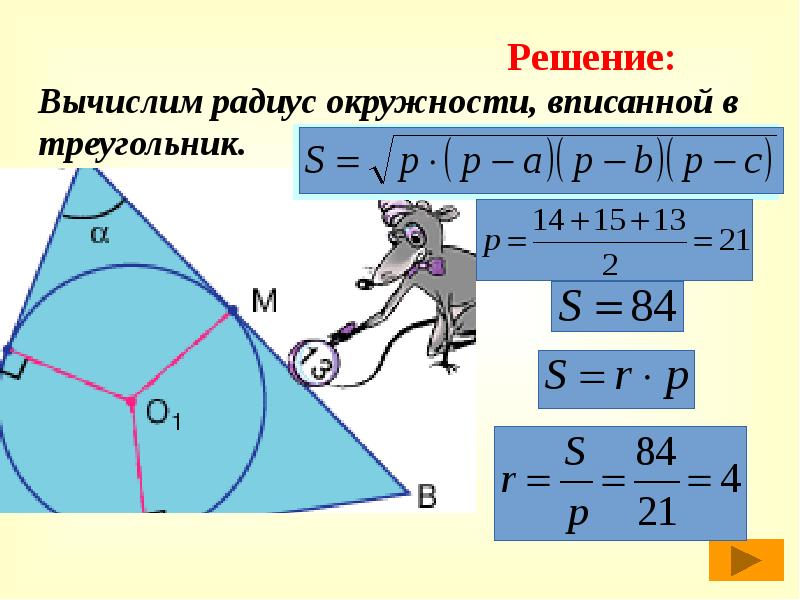
- 24. Вычислим радиус окружности, вписанной в треугольник. Вычислим радиус окружности, вписанной
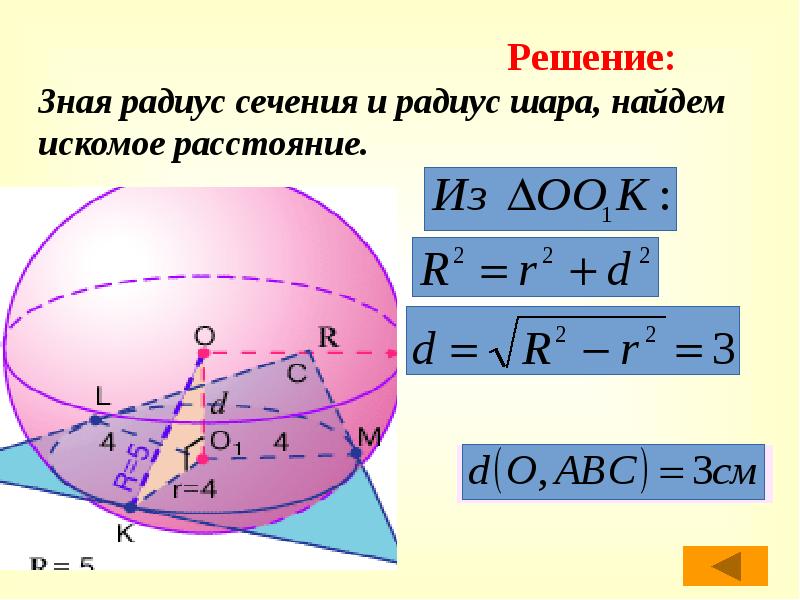
- 25. Зная радиус сечения и радиус шара, найдем искомое расстояние. Зная
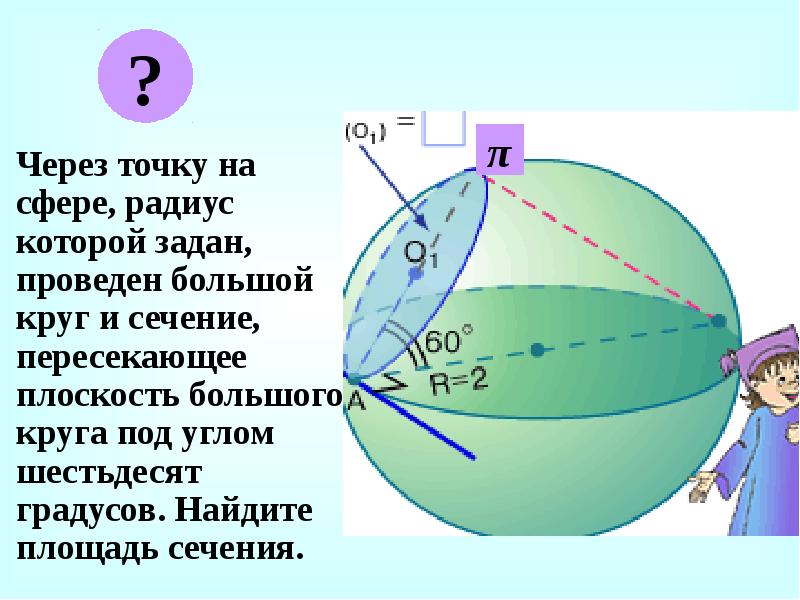
- 26. Через точку на сфере, радиус которой задан, проведен большой круг и
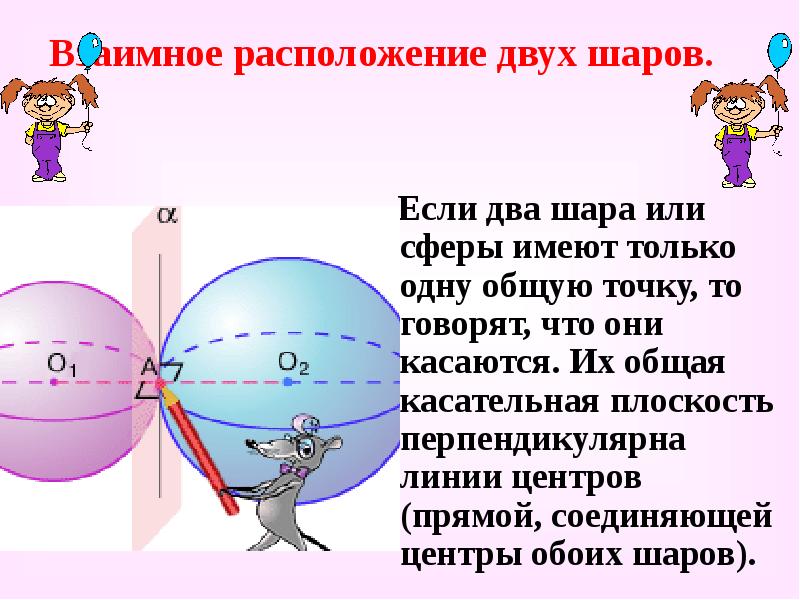
- 27. Взаимное расположение двух шаров. Если два шара или сферы имеют
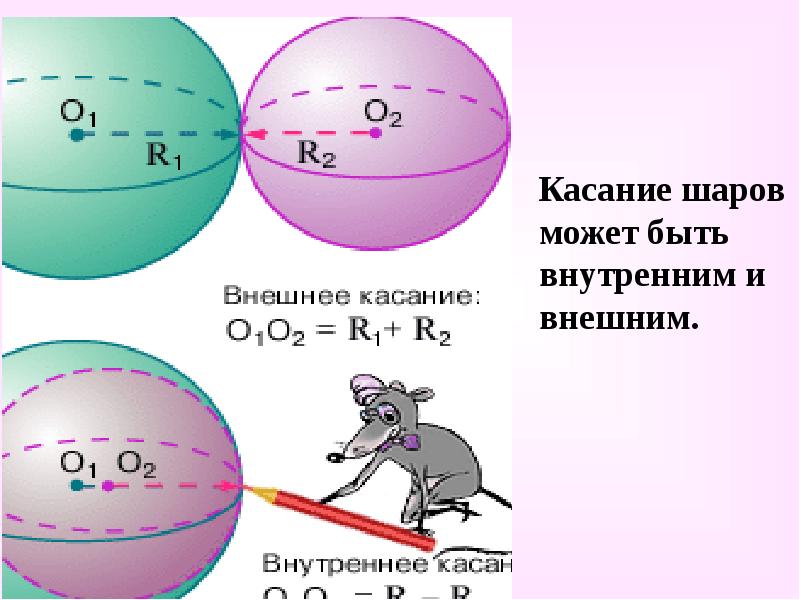
- 28. Касание шаров может быть внутренним и внешним. Касание шаров может
- 29. Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного
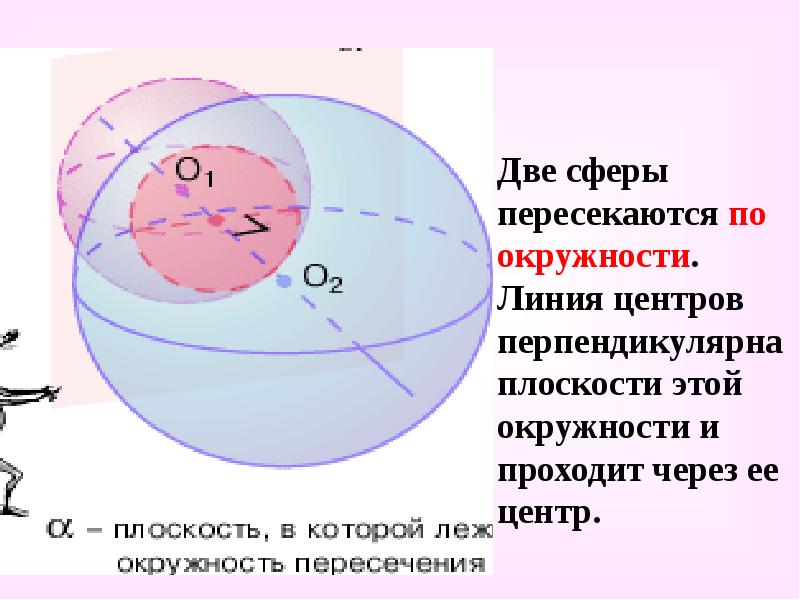
- 30. Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности
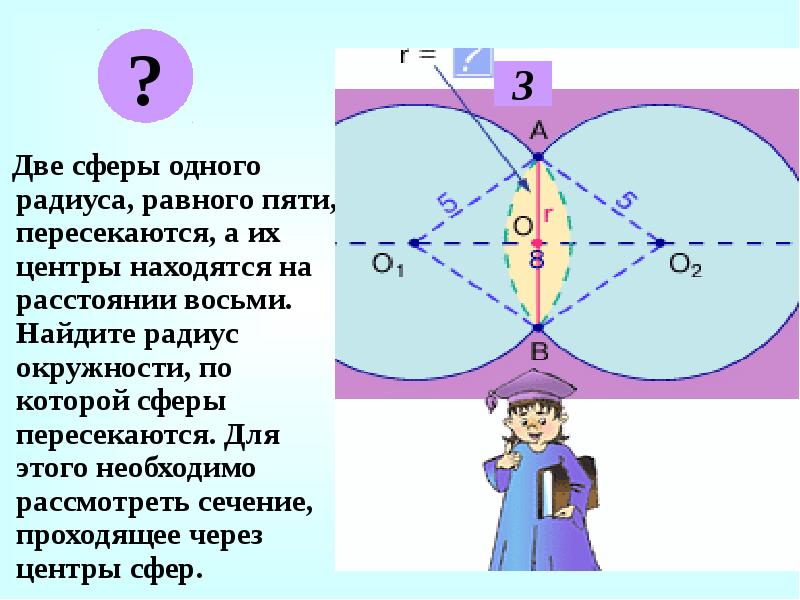
- 31. Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся
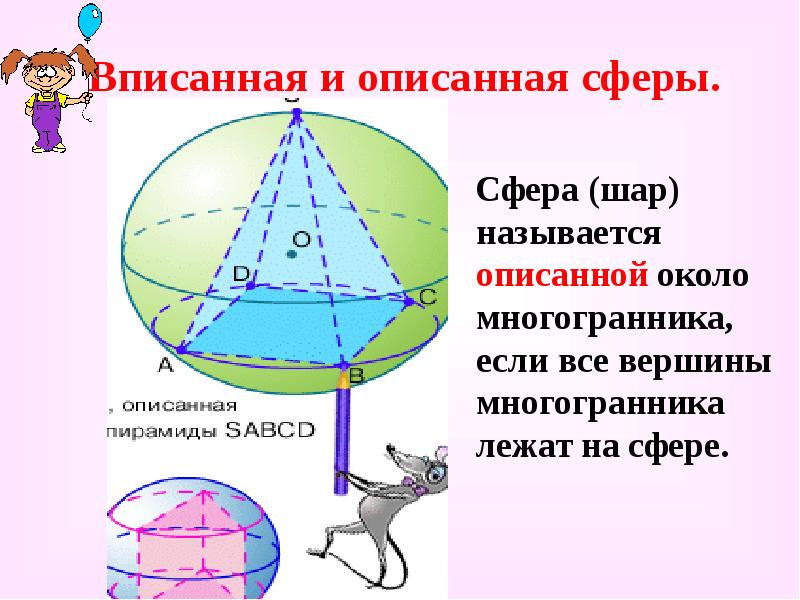
- 32. Вписанная и описанная сферы. Сфера (шар) называется описанной около многогранника,
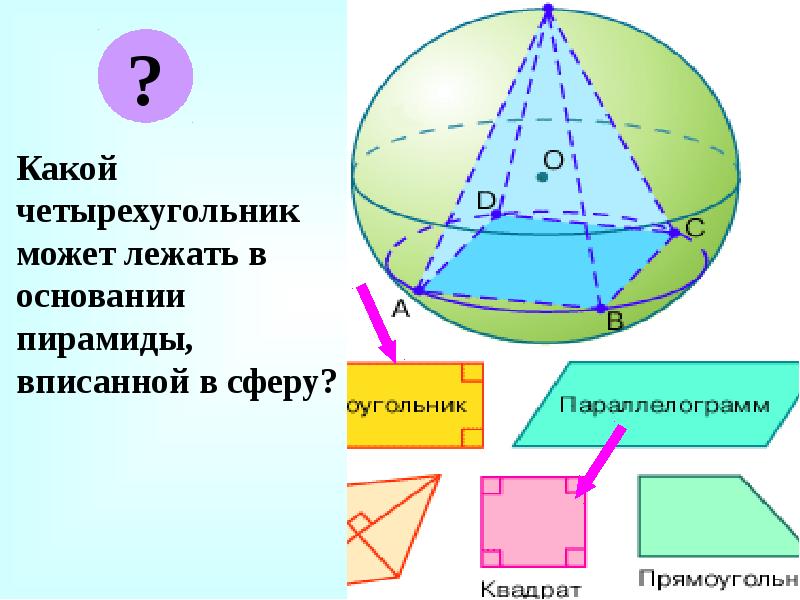
- 33. Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?
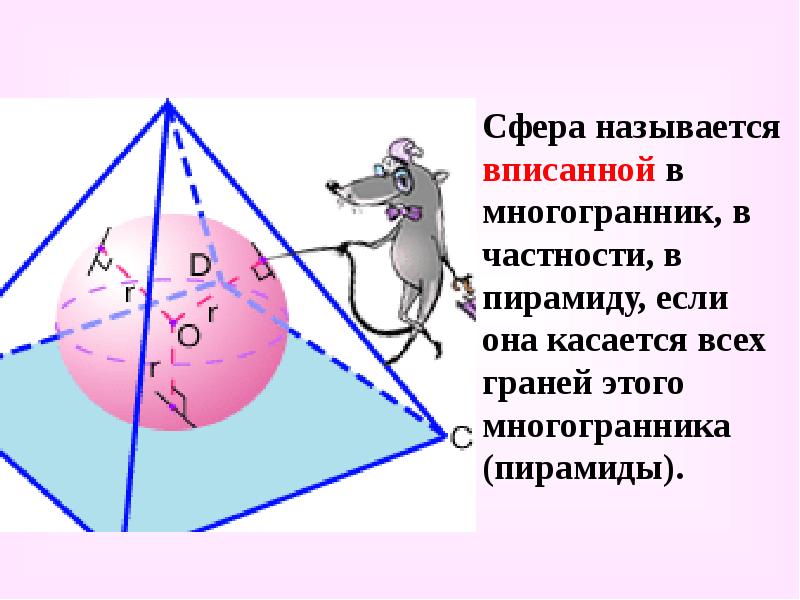
- 34. Сфера называется вписанной в многогранник, в частности, в пирамиду, если она
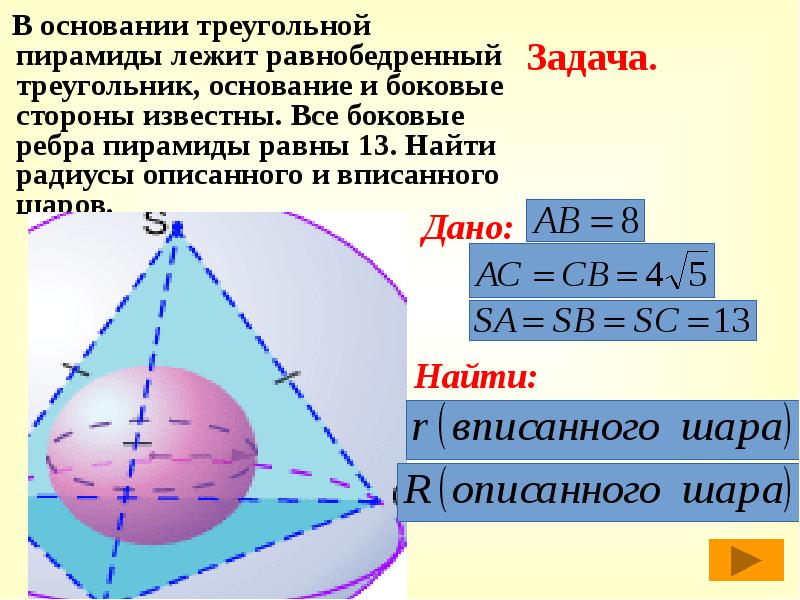
- 35. В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны
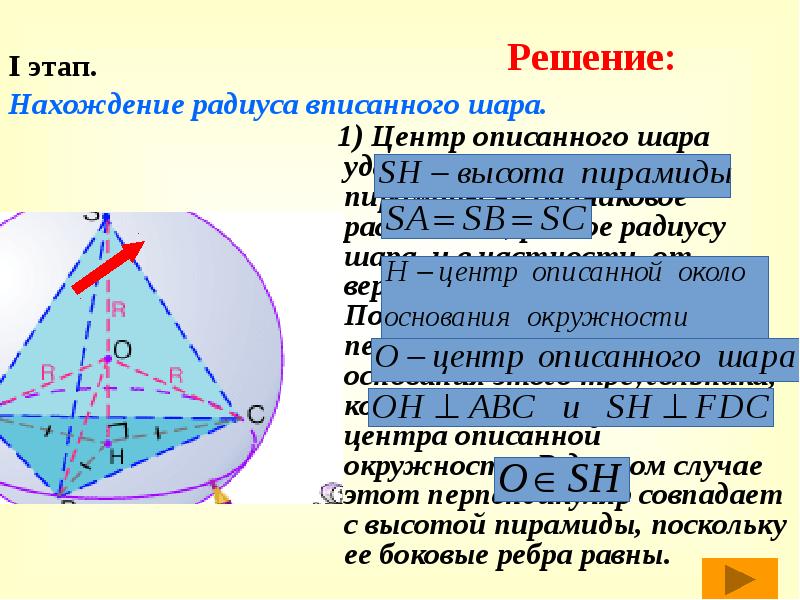
- 36. I этап. Нахождение радиуса вписанного шара. 1) Центр описанного шара
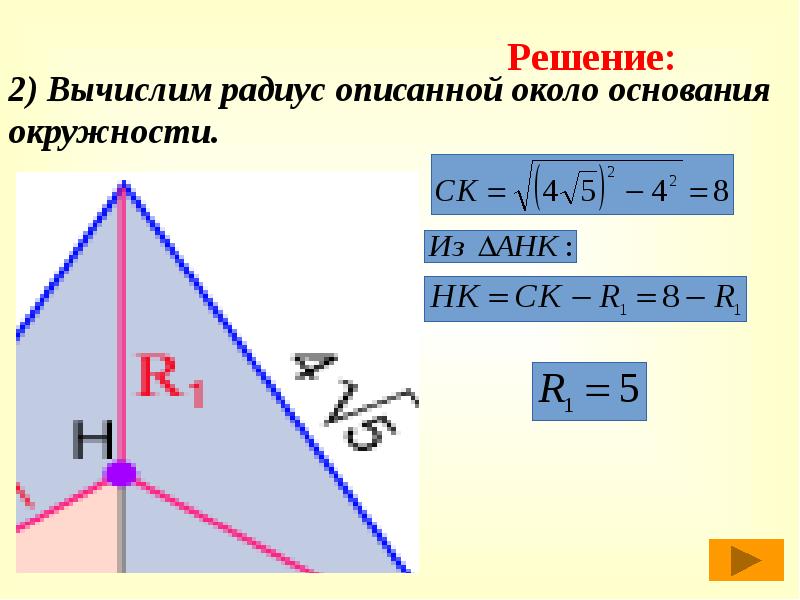
- 37. 2) Вычислим радиус описанной около основания окружности.
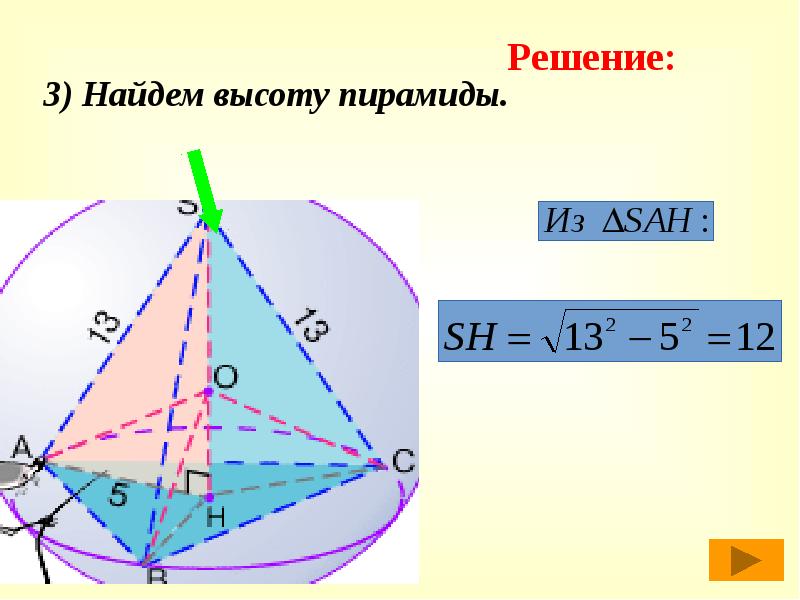
- 38. 3) Найдем высоту пирамиды.
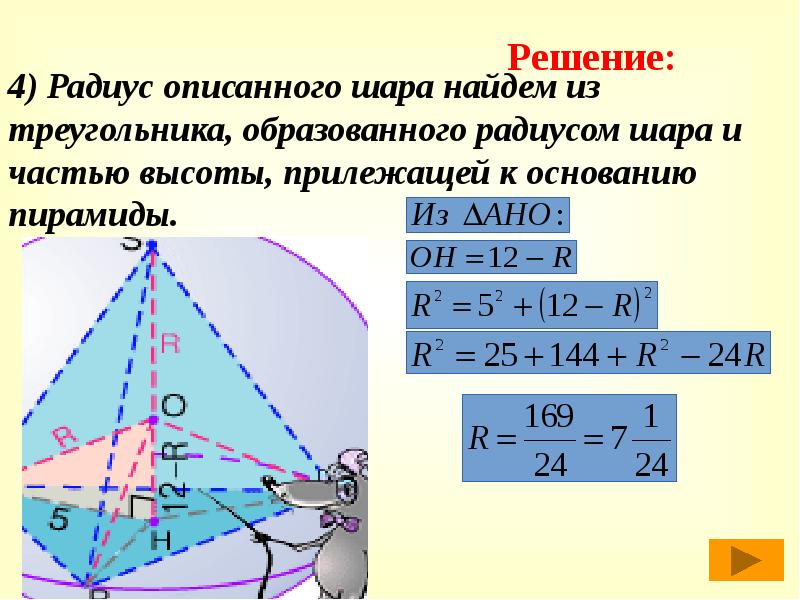
- 39. 4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и
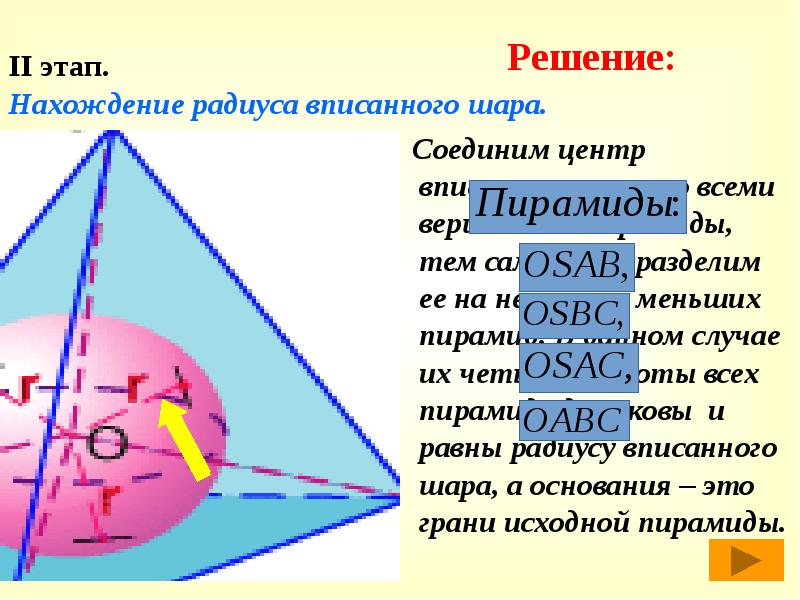
- 40. Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы
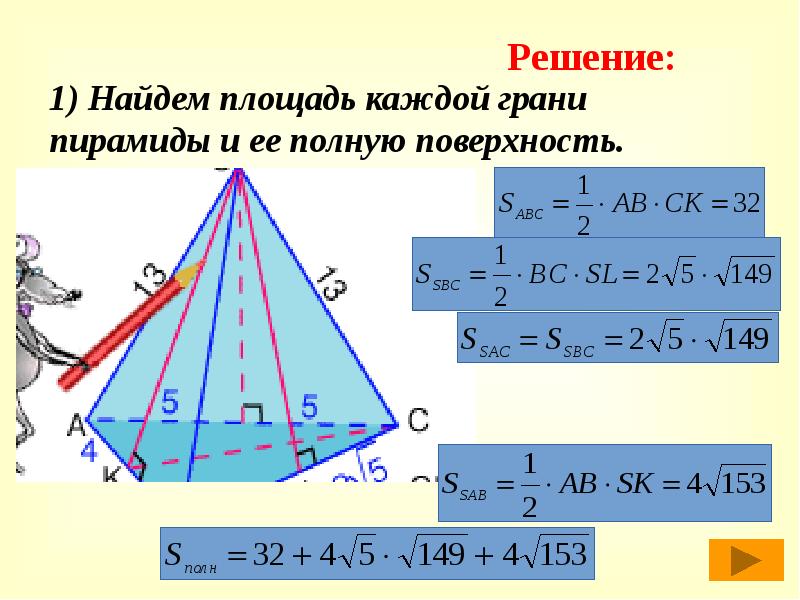
- 41. 1) Найдем площадь каждой грани пирамиды и ее полную поверхность.
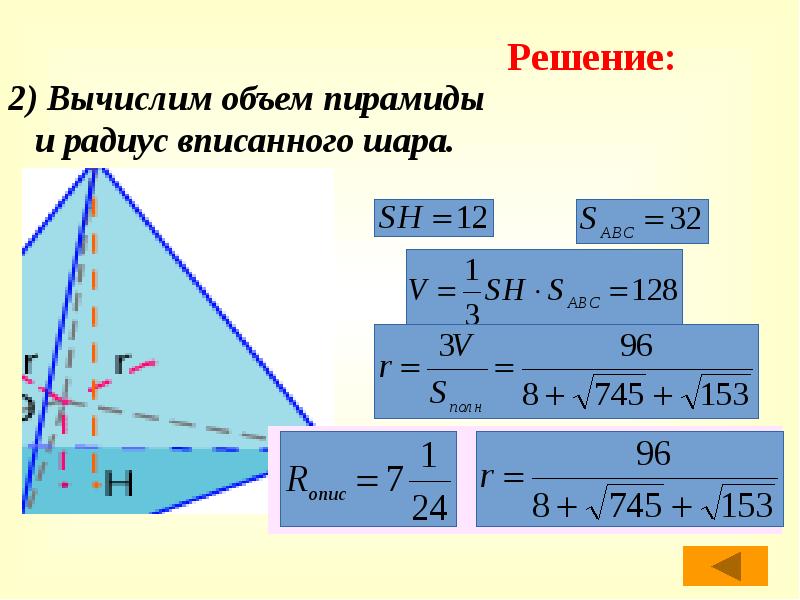
- 42. 2) Вычислим объем пирамиды и радиус вписанного шара.
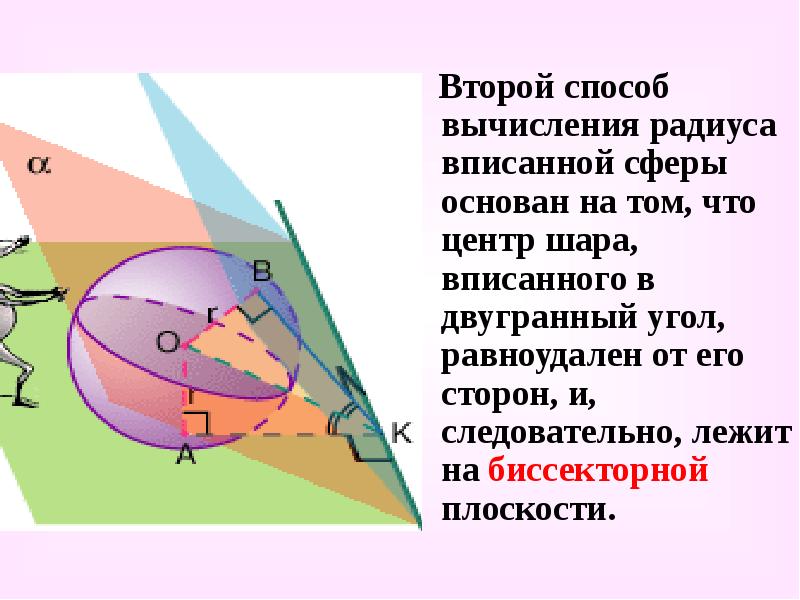
- 43. Второй способ вычисления радиуса вписанной сферы основан на том, что центр
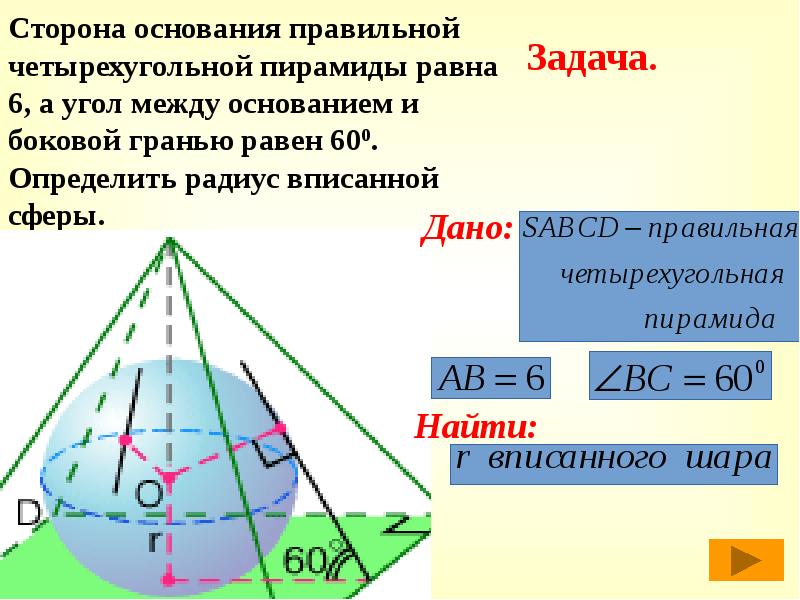
- 44. Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием
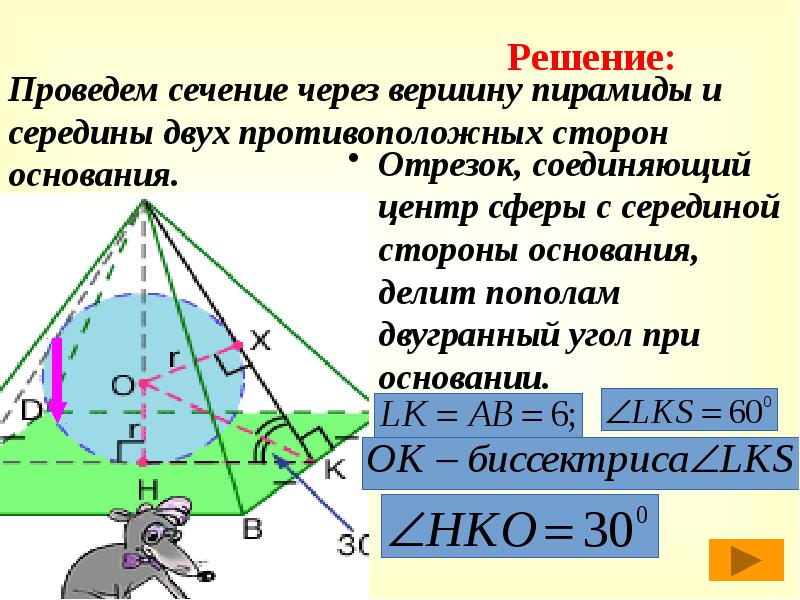
- 45. Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания.
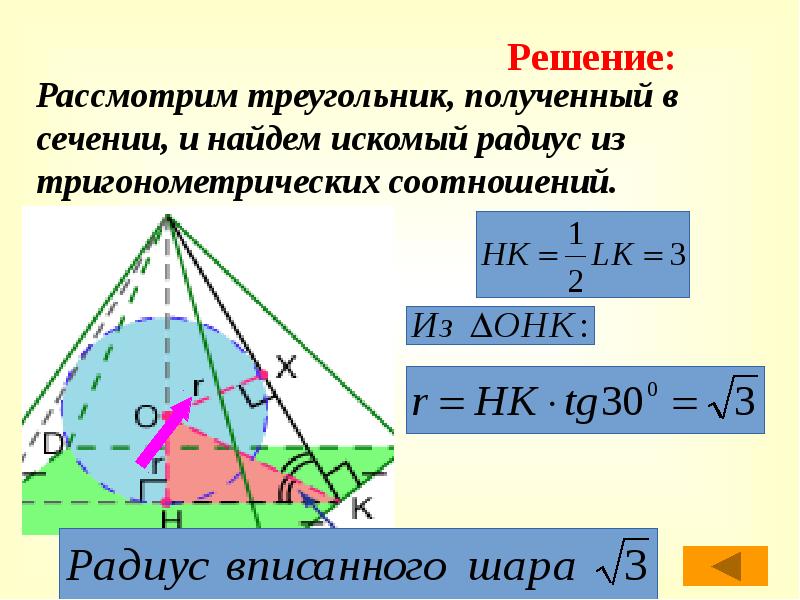
- 46. Рассмотрим треугольник, полученный в сечении, и найдем искомый радиус из тригонометрических
- 47. Итог урока Сегодня вы познакомились с: определением сферы, шара; взаимным
- 48. Заключение На этом наш урок закончен Спасибо за работу
- 49. Скачать презентацию




Слайды и текст этой презентации
Скачать презентацию на тему Тема урока: «Сфера и шар.» Цели : ввести понятие сферы, шара и их элементов; можно ниже:
Похожие презентации





























