Теоремы сложения и умножения вероятностей. Формула полной вероятности презентация
Содержание
- 2. Вероятность суммы событий Теорема сложения вероятностей двух событий. Вероятность суммы двух
- 3. Условные вероятности Пусть A и B – два события, рассматриваемые в
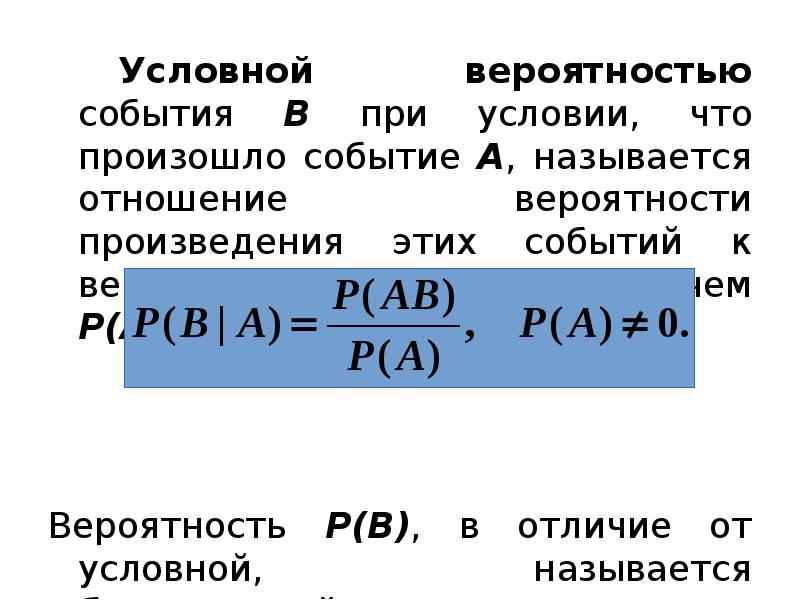
- 4. Условной вероятностью события B при условии, что произошло событие A, называется
- 5. Вероятность произведения событий Теорема умножения вероятностей Вероятность произведения двух событий равна
- 6. Событие A называется независимым от события B, если его условная вероятность
- 7. Пример Вероятность попадания в мишень для первого спортсмена равна 0,85, для
- 8. Решение Опыт: по мишени стреляют два спотртсмена. Пусть событие
- 9. а) Составим событие В={в мишень попадут оба спортсмена}= а) Составим событие
- 10. Так как а события независимы, то
- 11. Формула полной вероятности Рассмотрим n попарно несовместных событий для которых
- 12. Теорема. Пусть события Теорема. Пусть события образуют полную группу.
- 13. События обычно называют гипотезами, они исчерпывают все возможные предположения (гипотезы)
- 14. Пример В сборочный цех завода поступает 60% деталей из цеха
- 15. Решение. Опыт: в сборочный цех поступают детали из цеха №1 и
- 17. Схема Бернулли. Формула Бернулли. С понятием «независимых событий» связано понятие «независимых
- 18. Схема Бернулли Схема Бернулли Последовательность n независимых испытаний, в каждом из
- 19. Формула Бернулли Простейшая задача, относящаяся к схеме Бернулли, состоит в определении
- 20. Теорема. Теорема. Если производится n независимых испытаний, в каждом
- 21. Вероятность того, что в n опытах схемы Бернулли событие A появится
- 22. Предельные теоремы в схеме Бернулли Использование формулы Бернулли при больших значениях
- 23. Теорема Пуассона Теорема. Если число испытаний неограниченно увеличивается и вероятность p
- 24. Из предельного равенства (1) при больших n и малых p вытекает
- 25. Пример Вероятность изготовления нестандартной детали p=0,004. Найти вероятность того, что среди
- 26. Решение.
- 27. Локальная и интегральная теоремы Муавра-Лапласа В тех случаях, когда число испытаний
- 28. Теорема (Локальная теорема Муавра-Лапласа). Если вероятность p наступления события A в
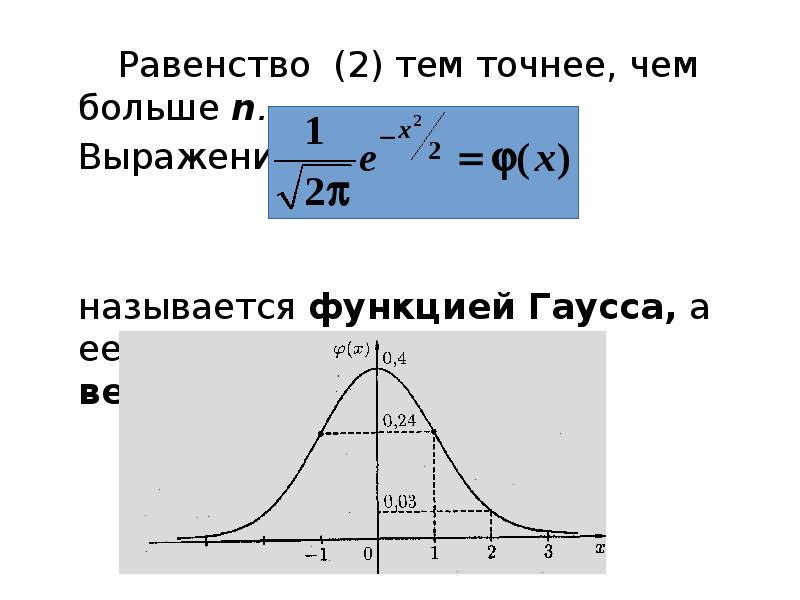
- 29. Равенство (2) тем точнее, чем больше n. Равенство (2) тем точнее,
- 30. Для функции составлены таблицы значений (они находятся, как правило, в
- 31. Пример Вероятность изделия детали первого сорта на данном станке равна 0,8.
- 32. По таблице Тогда
- 33. Теорема (Интегральная теорема Муавра—Лапласа). Теорема (Интегральная теорема Муавра—Лапласа). Если
- 34. Пример Производство дает 1% брака. Какова вероятность того, что из взятых
- 35. По таблице значений функции - функции Лапласа, получаем:
- 36. Скачать презентацию

































Слайды и текст этой презентации
Скачать презентацию на тему Теоремы сложения и умножения вероятностей. Формула полной вероятности можно ниже:
Похожие презентации





























