Тригонометрические формулы Обобщающий урок презентация

Тригонометрические формулы Обобщающий урок

Цель урока Повторить и систематизировать изученный материал Подготовиться к контрольной работе

Задачи урока Повторить определение синуса, косинуса, тангенса, котангенса числа α; Повторить формулы приведения, формулы двойного угла, формулы сложения; Повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом. Научить применять полученные знания при решении задач.

Ход урока Блиц-опрос Закрепление знаний и умений Самостоятельная работа (тест) Проверка самостоятельной работы Это интересно Итог урока Домашнее задание

Блиц-опрос Синусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α tg α = sin2 α +cos2 α= 1+ tg2 α= sin(-α)= tg (-α) = cos (α+β)= sin (α-β)= sin 2α= tg (α+β)= sin(π- α)= cos ( + α)=

Блиц-опрос Синусом угла α называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол α tg α = sin2 α +cos2 α = 1 1+ tg2 α = sin(-α) = - sin α tg (-α) = -tg α cos (α+β) = cosα cosβ – sinα sinβ sin (α-β) = sinα cosβ - cosα sinβ sin 2α = 2sin αcos α tg (α+β) = sin(π- α) =sin α cos ( + α) = -sinα

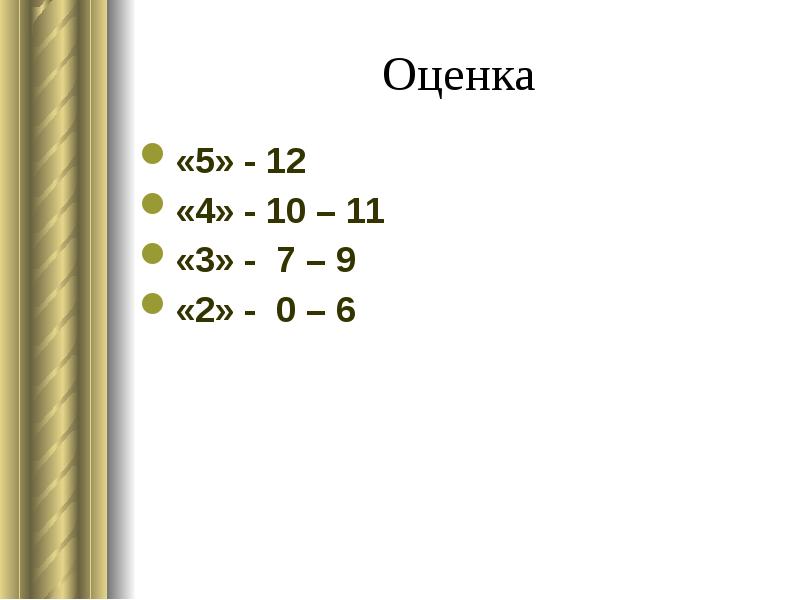
Оценка «5» - 12 «4» - 10 – 11 «3» - 7 – 9 «2» - 0 – 6

Закрепление знаний и умений №546 1) дано: найти: ОТВЕТ: 3) дано: найти: ОТВЕТ:

Упростить выражение Упростить выражение

№555 №555 1) Доказать: №557 Упростить выражение ОТВЕТ: № 564 1) Доказать:

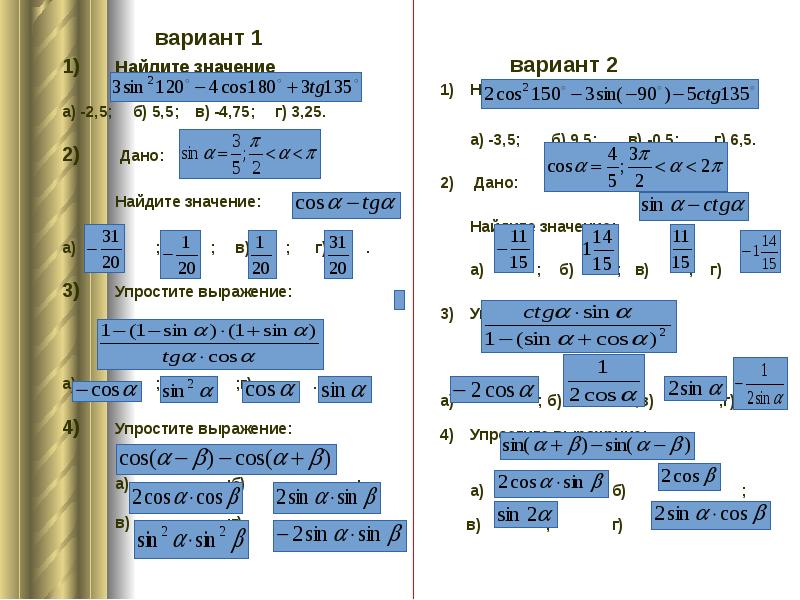
вариант 1 вариант 1 1) Найдите значение а) -2,5; б) 5,5; в) -4,75; г) 3,25. 2) Дано: Найдите значение: а) ;б) ; в) ; г) . 3) Упростите выражение: а) ;б) ;в) ;г) . 4) Упростите выражение: а) ;б) ; в) ;г)

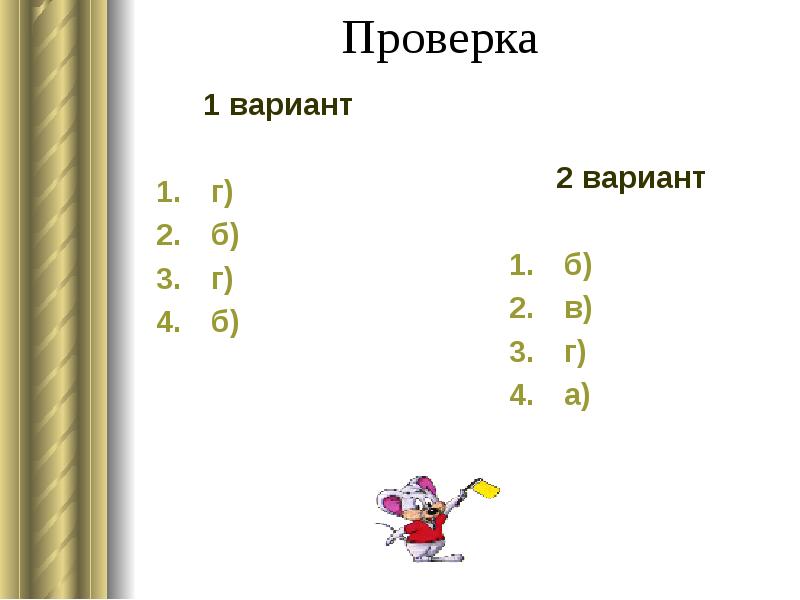
Проверка 1 вариант г) б) г) б)

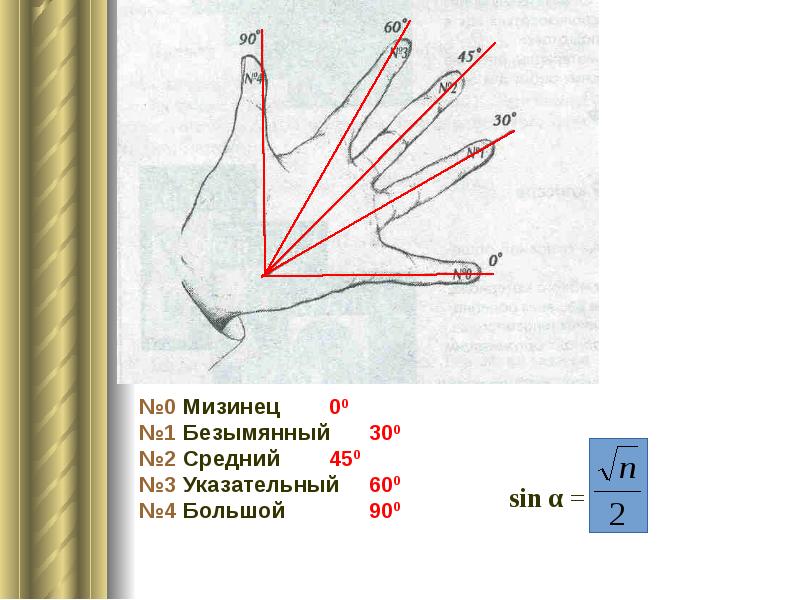
Это интересно Тригонометрия в ладони

Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников». Гиппарх является автором первых тригонометрических таблиц и одним из основоположников астрономии.

№0 Мизинец 00 №0 Мизинец 00 №1 Безымянный 300 №2 Средний 450 №3 Указательный 600 №4 Большой 900

Домашнее задание Проверь себя стр. 166

Спасибо, урок окончен!!! Спасибо, урок окончен!!!