Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые презентация
Содержание
- 6. Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.
- 7. Грани многогранника - это многоугольники, которые его образуют. Грани многогранника -
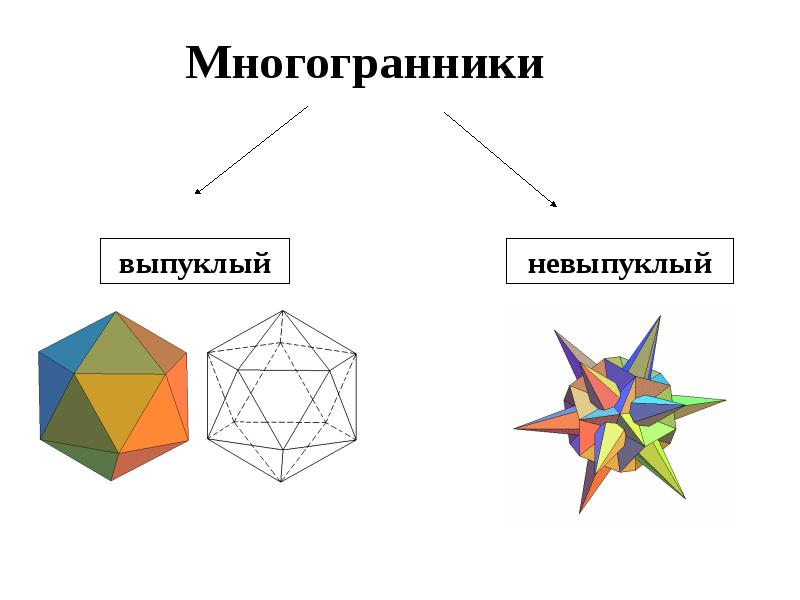
- 9. Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого
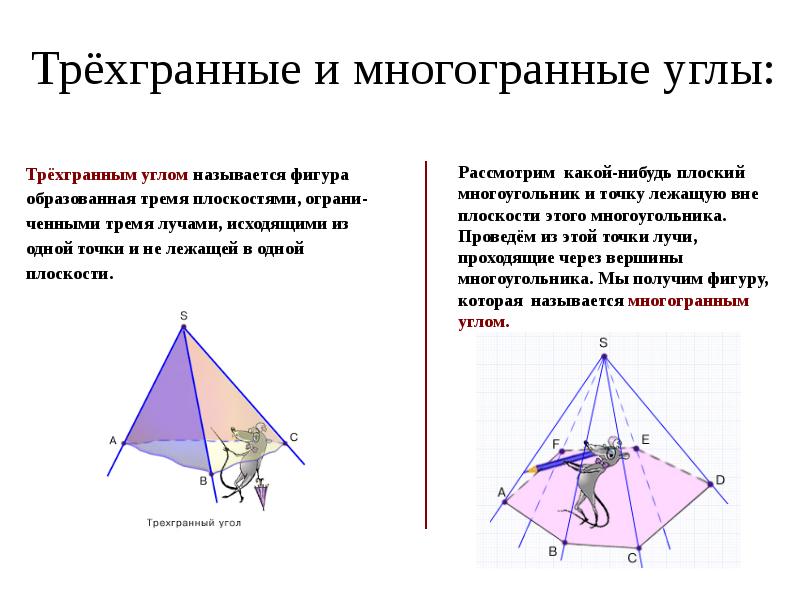
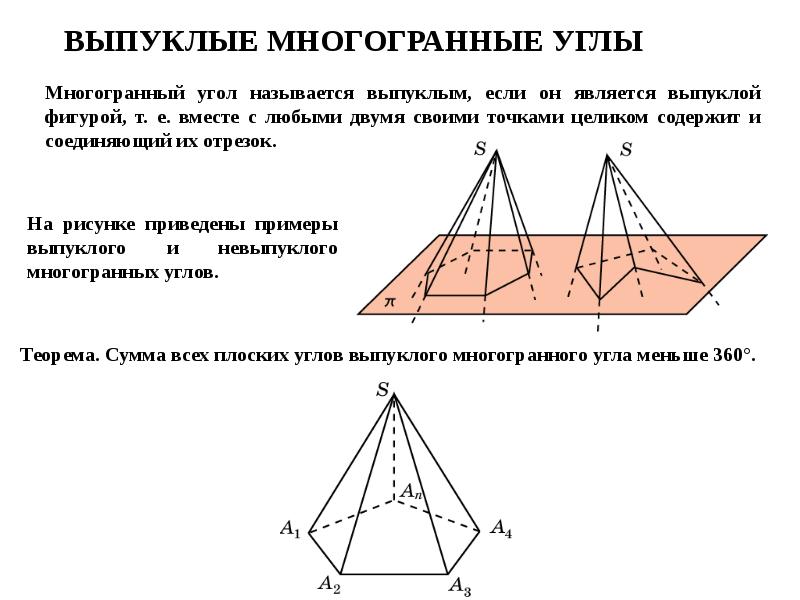
- 10. ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫ
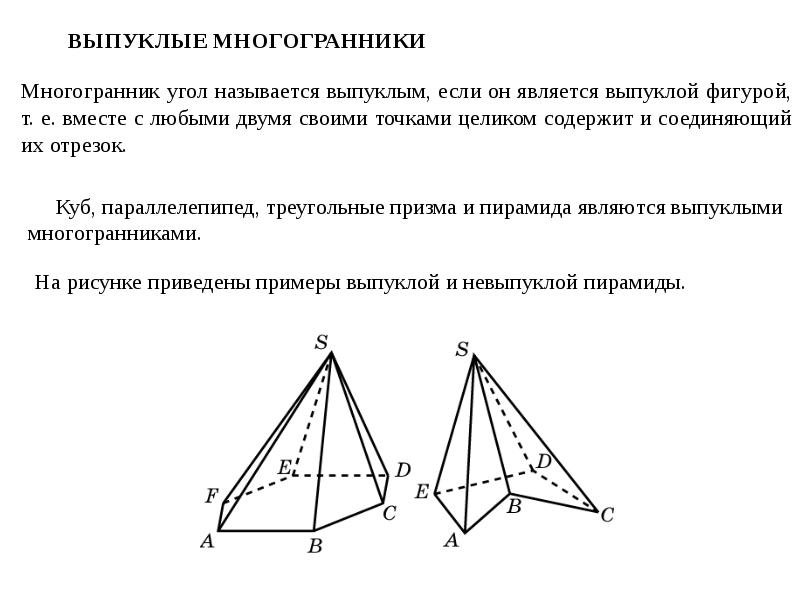
- 11. ВЫПУКЛЫЕ МНОГОГРАННИКИ
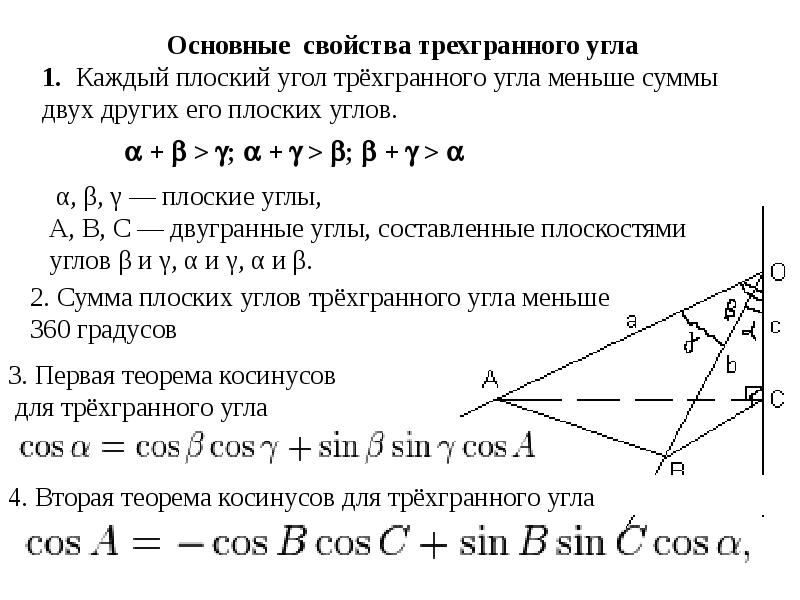
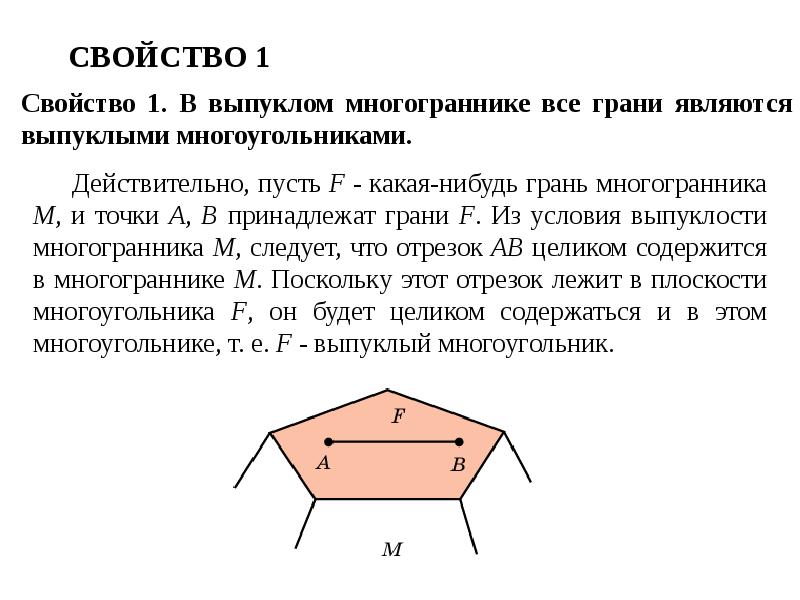
- 12. СВОЙСТВО 1
- 13. СВОЙСТВО 2
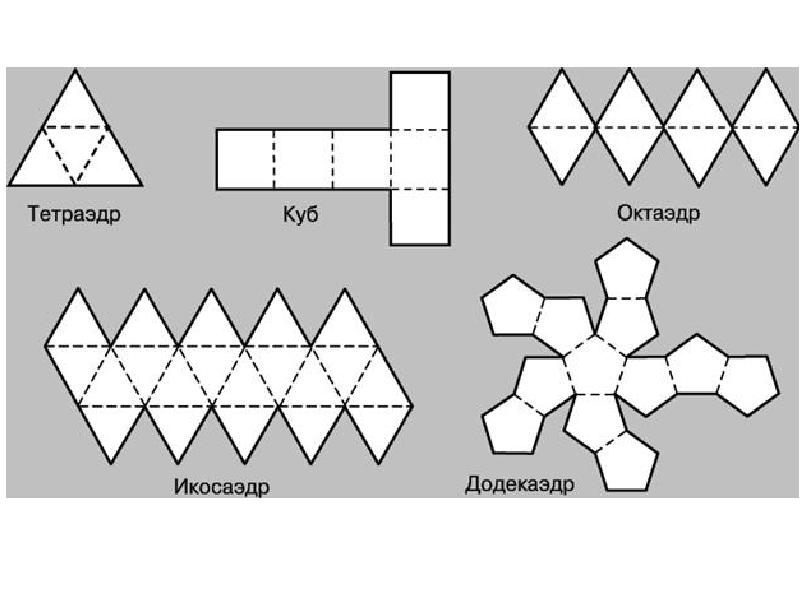
- 14. Правильные многогранники Если грани многогранника являются правильными многоугольниками с одним и
- 15. Названия многогранников пришли из Древней Греции, в них указывается
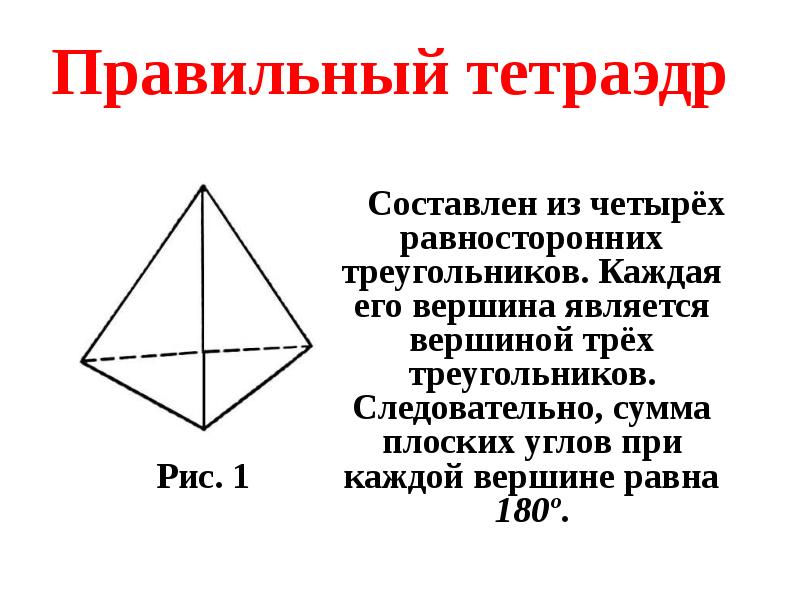
- 16. Правильный тетраэдр Составлен из четырёх равносторонних треугольников. Каждая его вершина
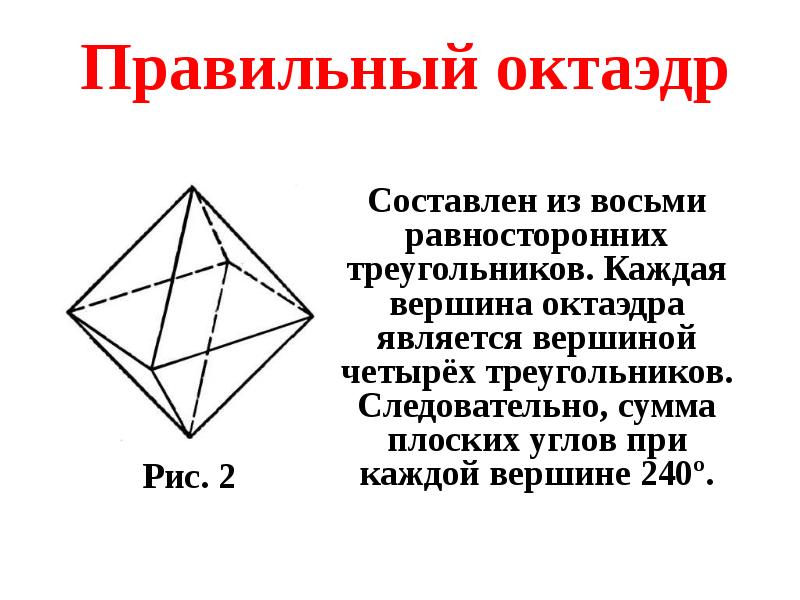
- 17. Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх
- 18. Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти
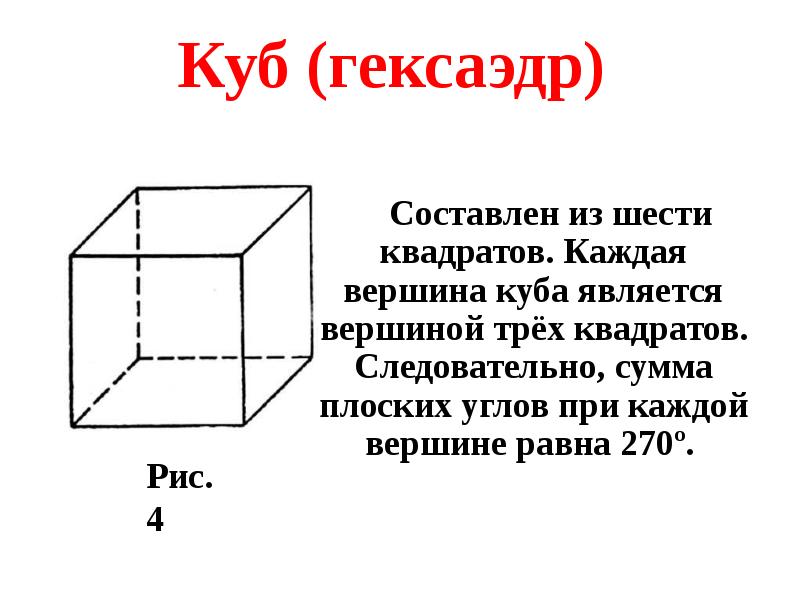
- 19. Куб (гексаэдр)
- 20. Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх
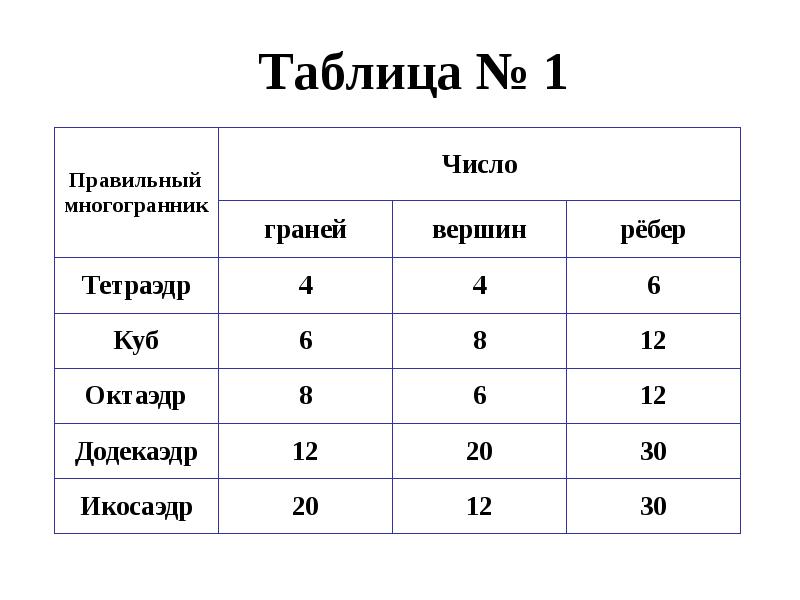
- 22. Сумма числа граней и вершин любого многогранника Сумма числа граней
- 26. Двойственность правильных многогранников Гексаэдр (куб) и октаэдр образуют двойственную пару многогранников.
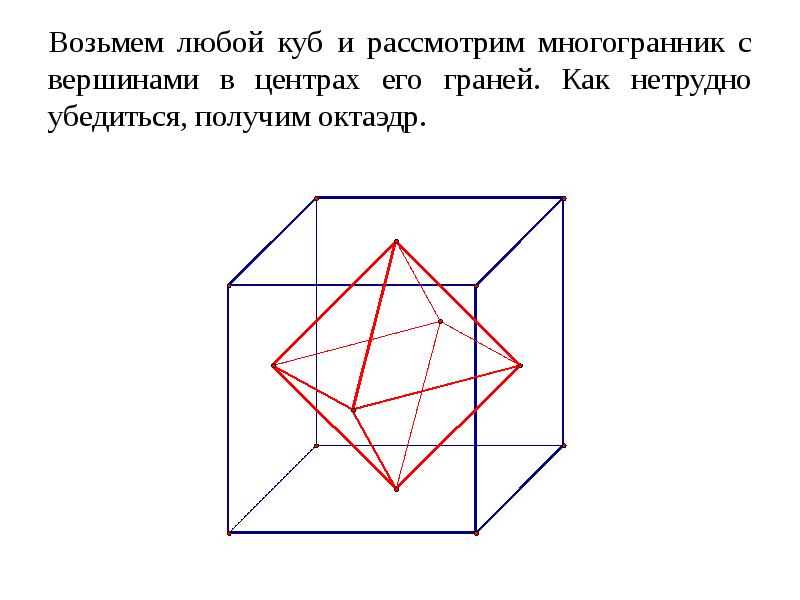
- 27. Возьмем любой куб и рассмотрим многогранник с вершинами в центрах его
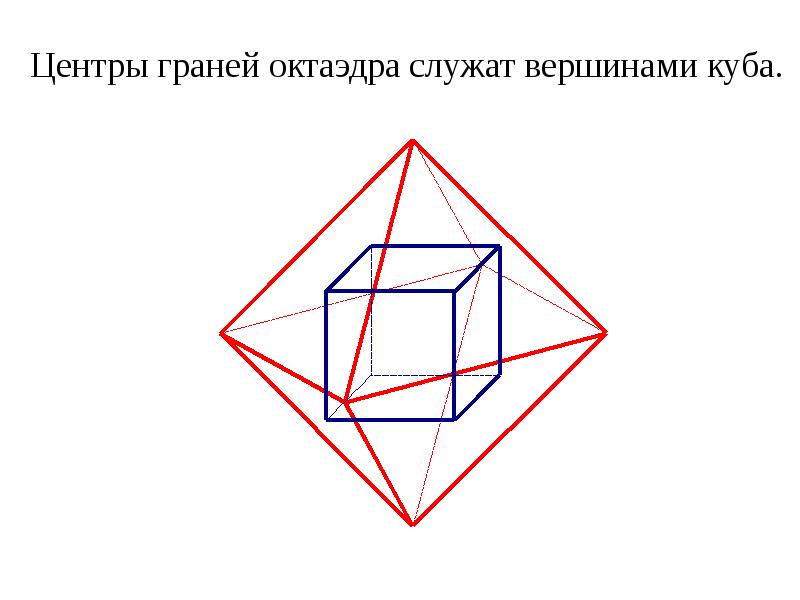
- 28. Центры граней октаэдра служат вершинами куба. Центры граней октаэдра служат вершинами
- 29. Сурьменистый сернокислый натрий – тетраэдра. Сурьменистый сернокислый натрий – тетраэдра.
- 34. Скачать презентацию



















Слайды и текст этой презентации
Скачать презентацию на тему Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые можно ниже:
Похожие презентации





























