Выпуклые функции – определение. Понятие о точке перегиба, необходимое условие презентация

Выпуклые функции – определение. Понятие о точке перегиба, необходимое условие перегиба. Выполнила: студентка 1 курса Наумова А. Группа: ИИЯ-19 Преподаватель(проверила): Волкова Н.А.

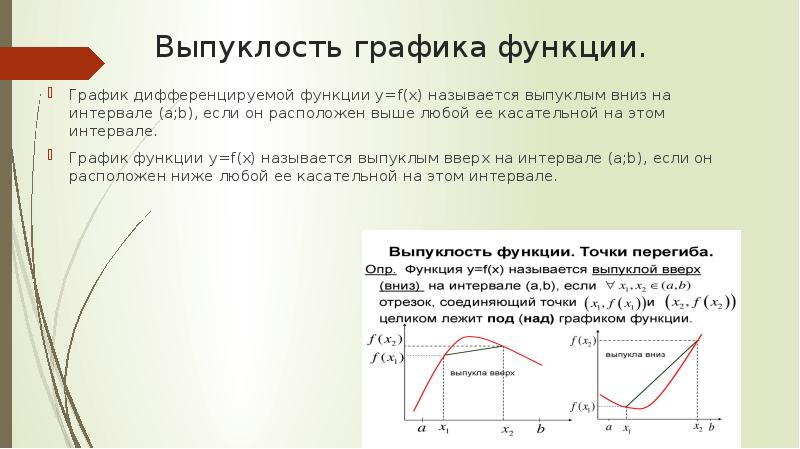
Выпуклость графика функции. График дифференцируемой функции y=f(x) называется выпуклым вниз на интервале (a;b), если он расположен выше любой ее касательной на этом интервале. График функции y=f(x) называется выпуклым вверх на интервале (a;b), если он расположен ниже любой ее касательной на этом интервале.

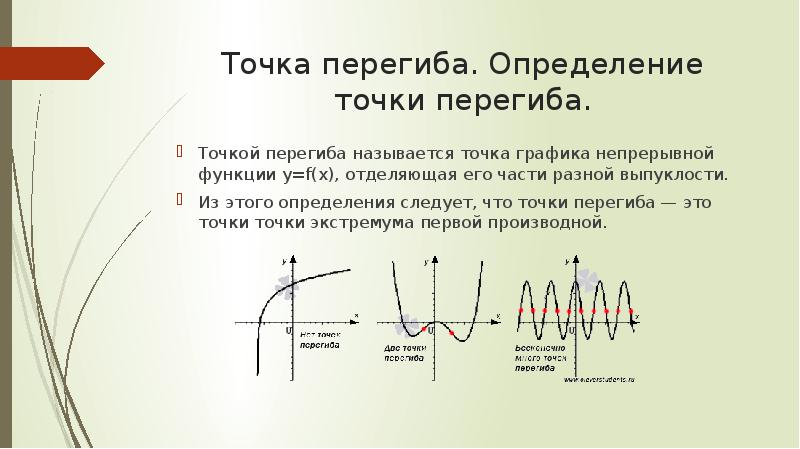
Точка перегиба. Определение точки перегиба. Точкой перегиба называется точка графика непрерывной функции y=f(x), отделяющая его части разной выпуклости. Из этого определения следует, что точки перегиба — это точки точки экстремума первой производной.

Теорема: Если функция y=f(x) во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. f″(x)<0,то график функции в этом интервале выпуклый вверх. Если же f″(x)>0 ꓯx∈ (a;b)- график выпуклый вниз. Доказательство. Пусть f″(x)<0 ꓯx∈ (a;b). Возьмем на графике функции произвольную точку М с абсциссой xₒ ∈ (a;b). Проведем через точку М касательную. Сравним в точке x∈ (a;b) ординату y кривой y=f(x) с ординатой y ее касательной.

Теорема(необходимое условие перегиба) Для того, чтобы точка xₒ являлась точкой перегиба дважды дифференцируемой функции y=f(x), необходимо, чтобы ее вторая производная в этой точке равнялась нулю( f″(xₒ)=0) или не существовала.

Если точка xₒ-точка перегиба функции f(x) и если Ǝf″(x) в некоторой окрестности точки xₒ(непрерывная в точке xₒ),то f″(xₒ)=0. Если точка xₒ-точка перегиба функции f(x) и если Ǝf″(x) в некоторой окрестности точки xₒ(непрерывная в точке xₒ),то f″(xₒ)=0. Доказательство: Докажем методом от противного, т.е предположим, что  f″(xₒ)≠0. Тогда f″(xₒ)<0 либо f″(xₒ)>0 . По условию f″ непрерывна в точке xₒ→по свойству сохранения знака непрерывной функции получим : Ǝδ:ꓯx ∈ U(δ) (xₒ), sign f″(x)= sign f″(xₒ) т.е. по достаточному условию строгой выпуклости f″(x)>0 ꓯx ∈ (a;b) (функция выпукла вниз) или f″(x)<0 ꓯx ∈ (a;b)(функция выпукла вверх). Это противоречит определению точки перегиба, которое гласит, что при переходе через точку xₒ направление выпуклости меняется.