מהי לוגיקה презентация
Содержание
- 2. לוגיקה במדעי המחשב מחשב מחקה יכולת שכלית (היגיון) תוכנית מחשב –
- 3. טיעונים אם רכבת מאחרת וגם אין מוניות זמינות בתחנה, אז אלי
- 4. תחשיב הפסוקים נדון בפסוקיי חיווי, אשר יש להם בדיוק אחד משני
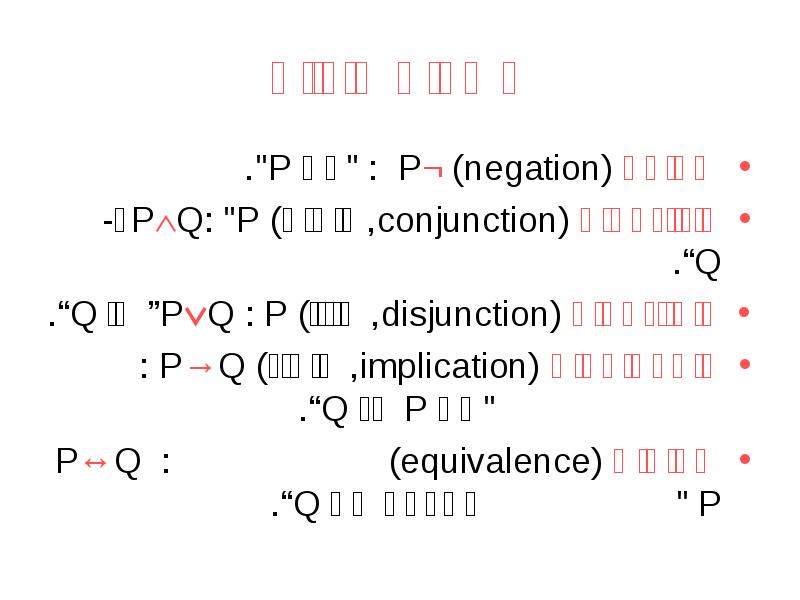
- 5. קשרים לוגיים שלילה (negation) ¬P : "לא P". קוניונקציה (conjunction, גימום)
- 6. תחביר הגדרה: נוסחא נקראת בנויה היטב (well-formed formula) אם ניתן ליצור
- 7. פסוקים מורכבים דוגמא: ,(pq) ,((pq)(¬p)) ,((¬p)q) ¬(¬p))) ולא ((p
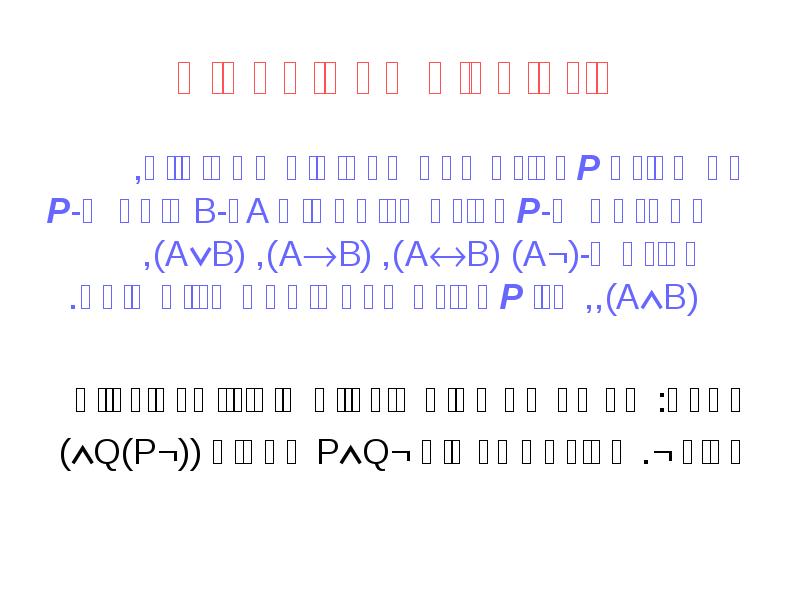
- 8. אינדוקציה על נוסחאות אם תכונה P נכונה לכל הפסוקים האטומיים, ומהנחה
- 9. הצרנה זהו מקס או שההוא מוריץ ואני ליצן: p q
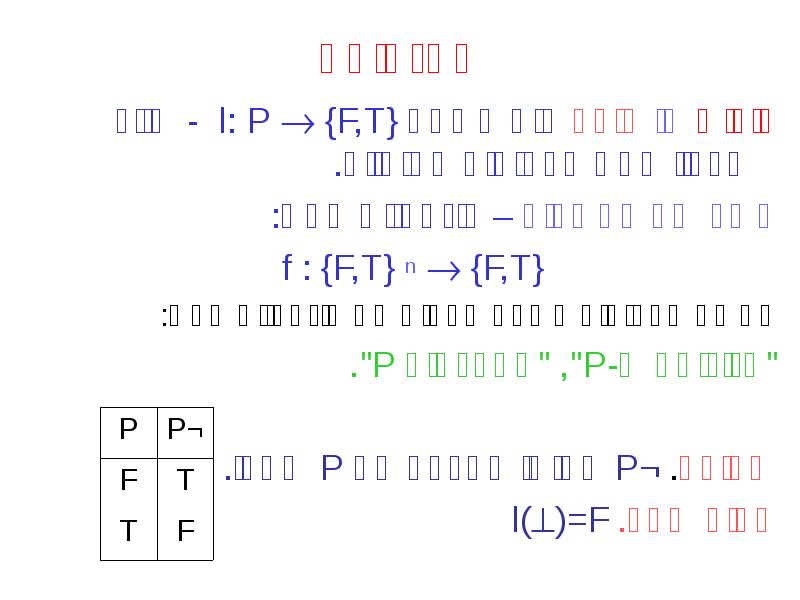
- 10. סמנטיקה פירוש או מודל הוא השמה l: P {F,T} -
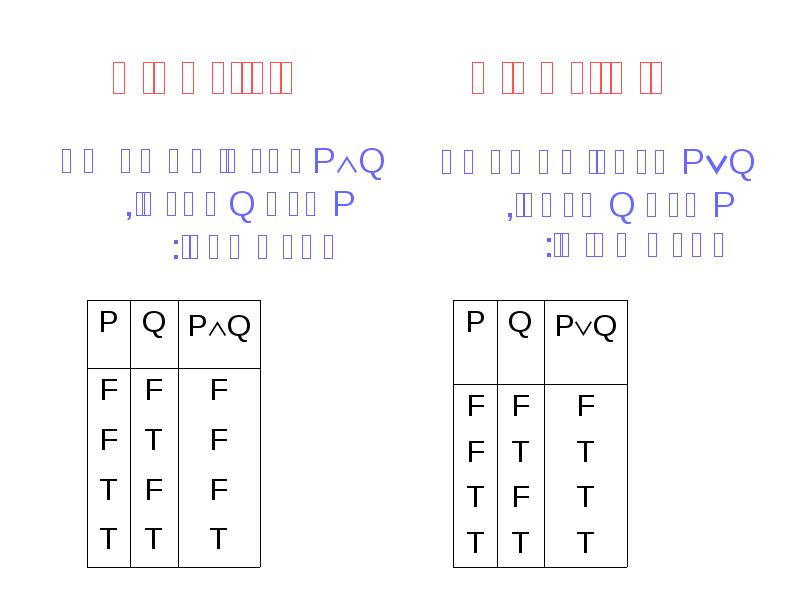
- 11. דיסיונקציה קוניונקציה PQ אמיתי כאשר גם P וגם Q
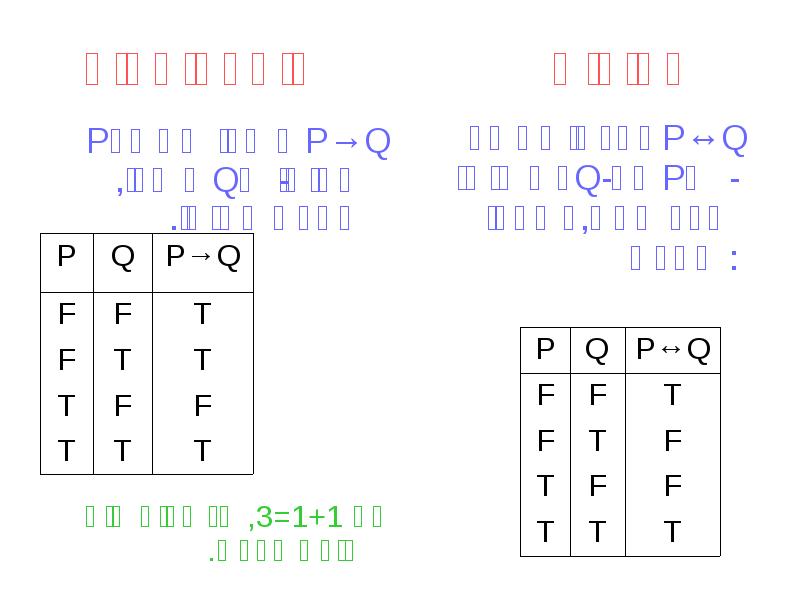
- 12. שקילות אימפליקציה P→Q שקרי כאשר P אמיתי
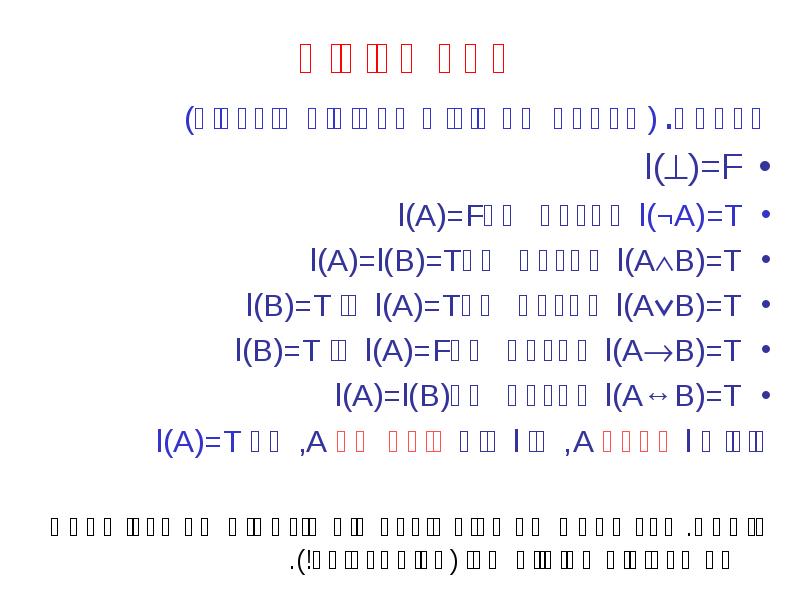
- 13. יחס ספיקות הגדרה. (הרחבה של פירוש לפסוקים מורכבים) l()=F l(¬A)=T אם
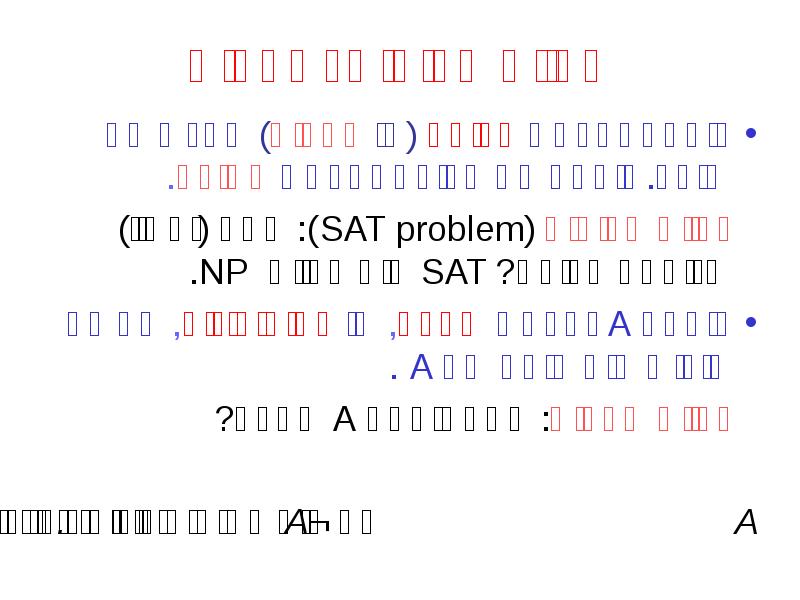
- 14. בעיות ספיקות ותקפות נוסחה נקראת ספיקה (או עקבית) אם יש לה
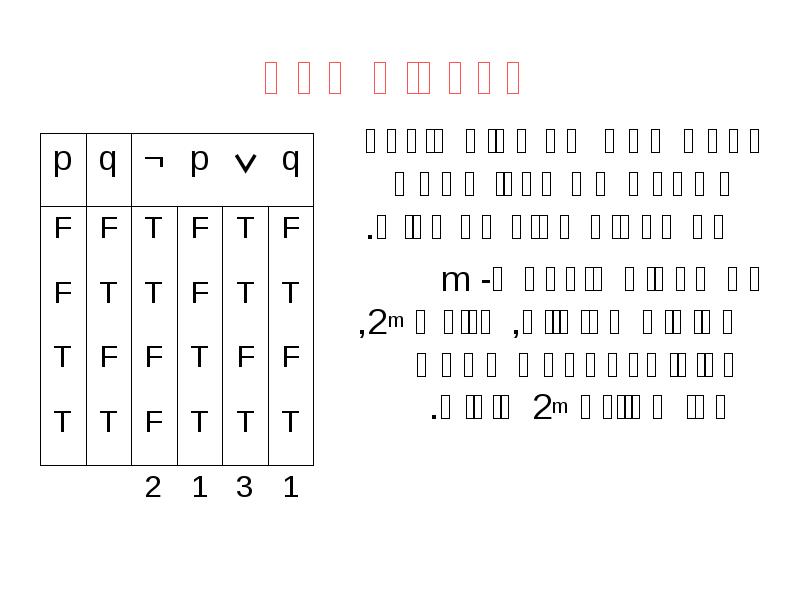
- 15. טבלאות אמת טבלת אמת של פסוק מורכב מתארת את ערכי האמת
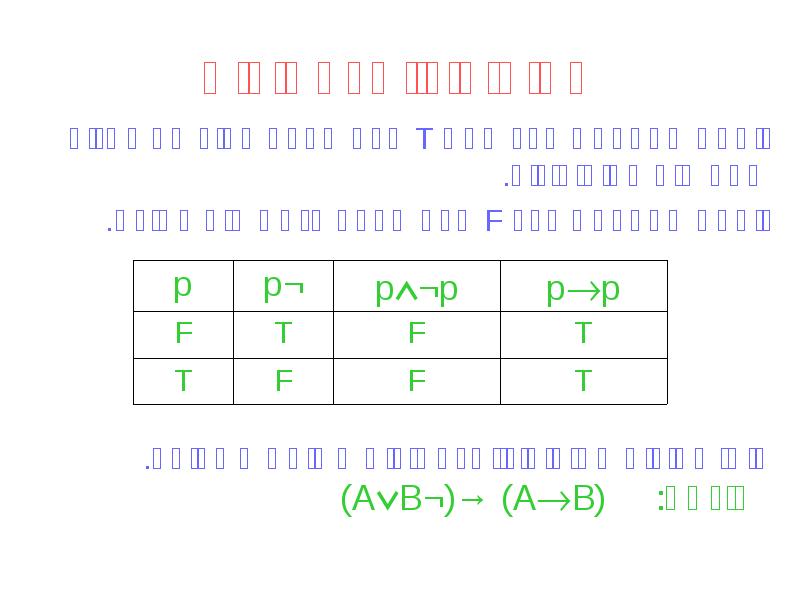
- 16. טאוטולוגיות וסתירות נוסחה המקבלת ערך אמת T לכל הצבה עבור המשתנים
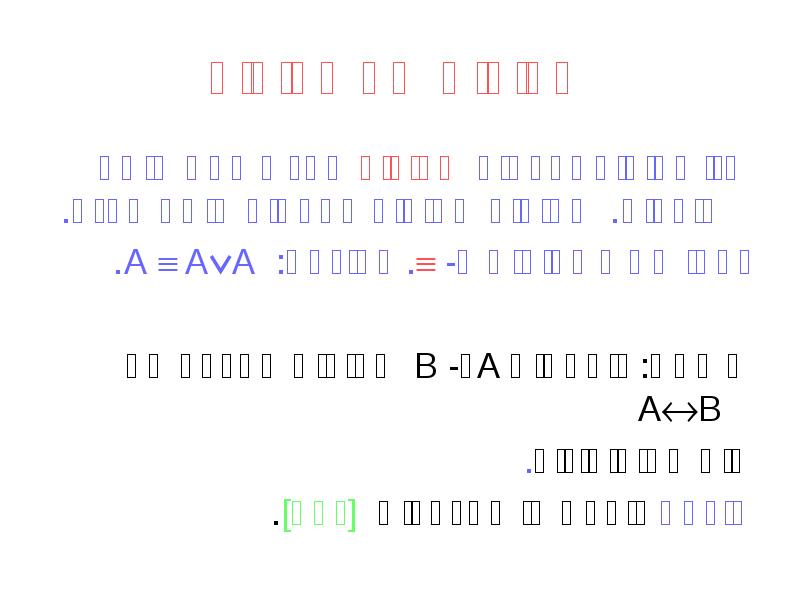
- 17. שקילות של פסוקים שני פסוקים נקראים שקולים אם יש להם אותם
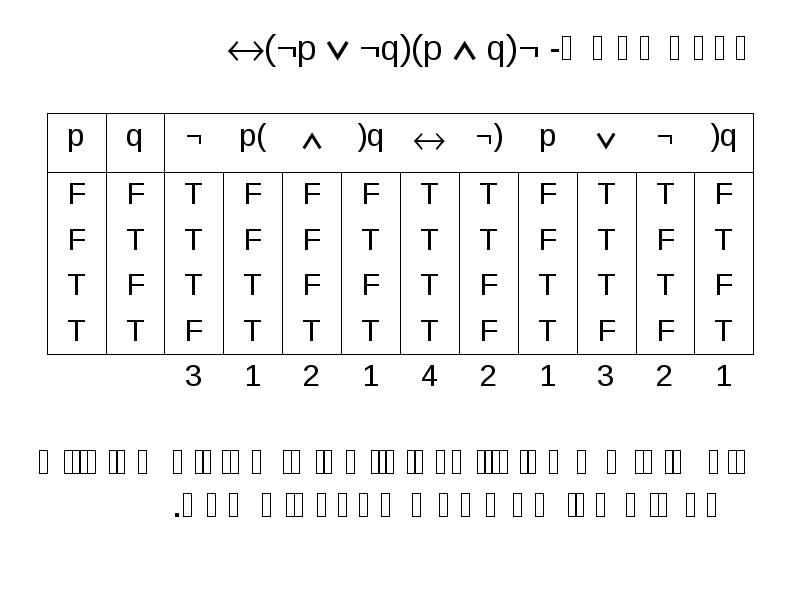
- 18. טבלת אמת ל- ¬(p q)(¬p ¬q) טבלת אמת ל-
- 19. שקילויות יסודיות
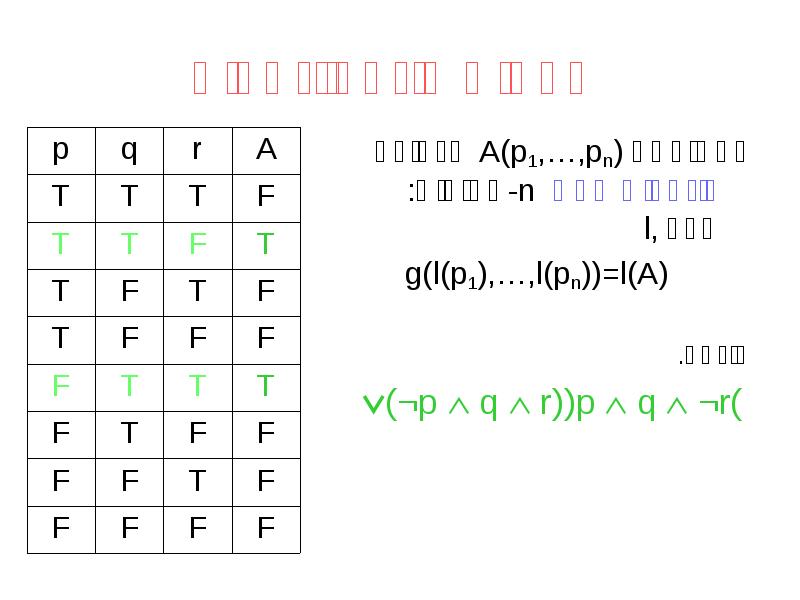
- 20. שלמות פונקציונאלית כל נוסחה A(p1,…,pn) מגדירה פונקצית אמת n-מקומית: לכל ,l
- 21. משפת (שלמות פונקציונאלית). לכל פונקצית אמת קיימת נוסחה המגדירה אותה. משפת
- 22. קבוצות שלמות של קשרים הגדרה: קבוצה של קשרים שבאמצעותם ניתן לתאר
- 23. קבוצות לא שלמות של קשרים למה. {,,, } היא קבוצה לא
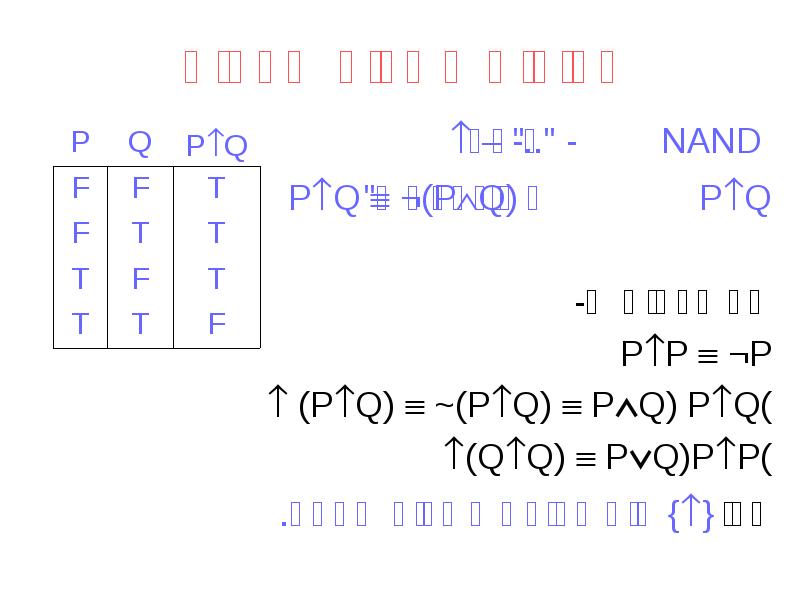
- 24. קבוצות קשרים שלמות NAND – "לא ו-.." - PQ מוגדרת
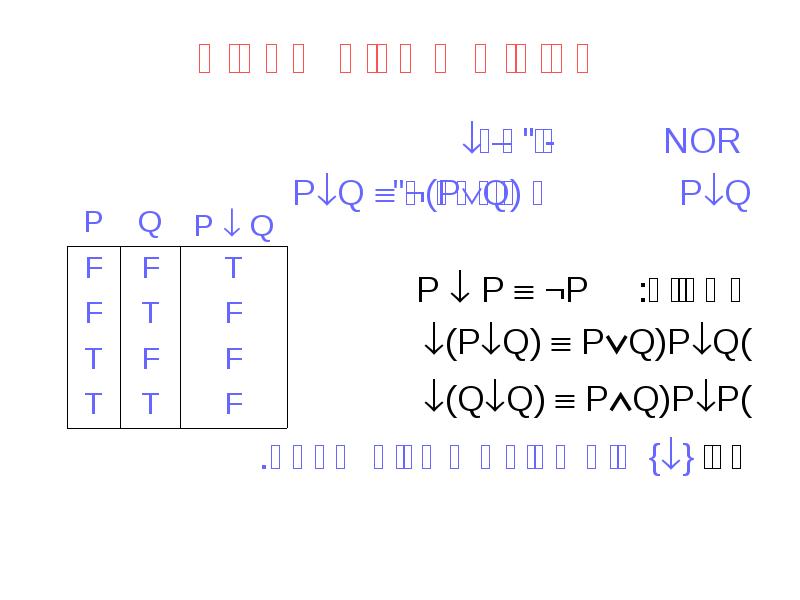
- 25. קבוצות קשרים שלמות NOR – "לא או" - PQ מוגדר
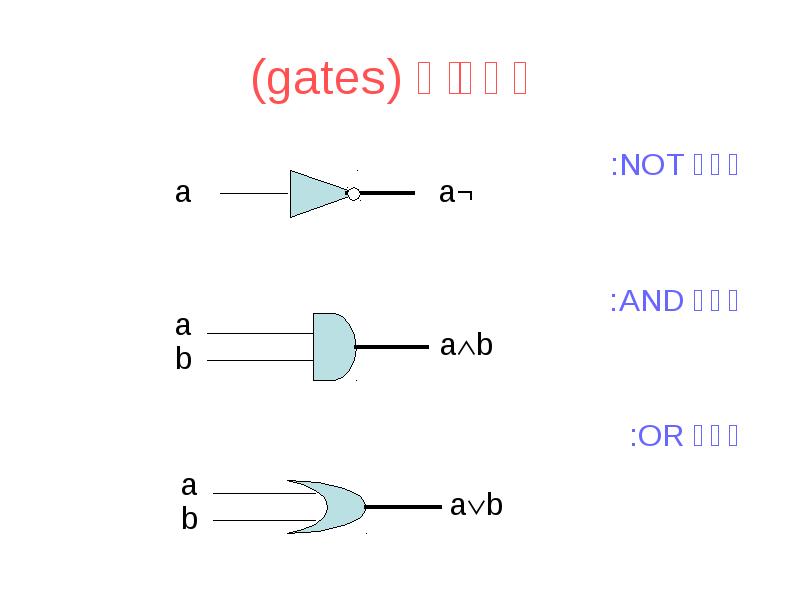
- 26. שערים (gates) שער NOT: שער AND: שער OR:
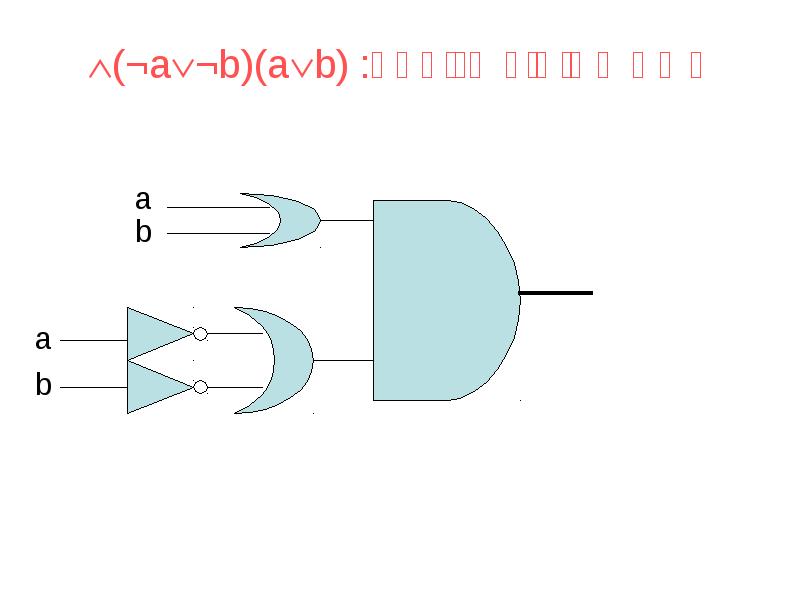
- 27. רשת לתיאור הנוסחה: (ab)(¬a¬b)
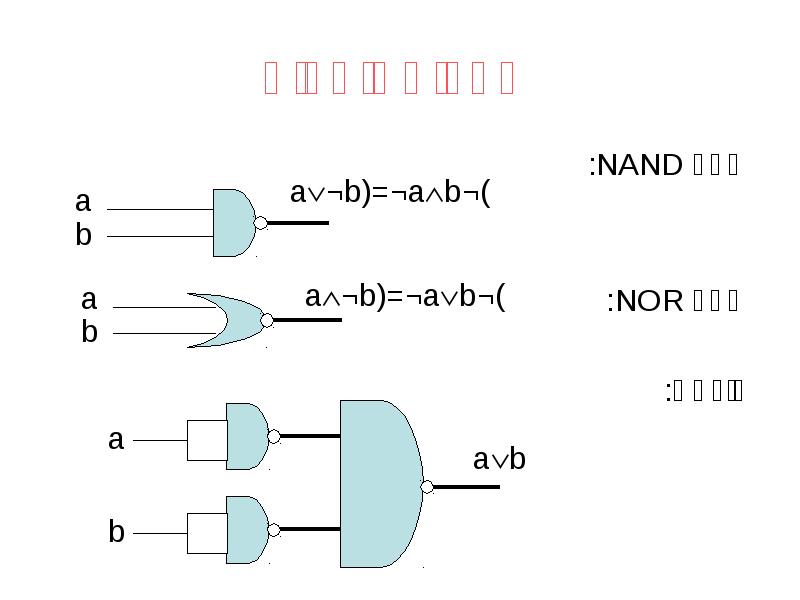
- 28. שערים נוספים שער NAND: שער NOR: דוגמא:
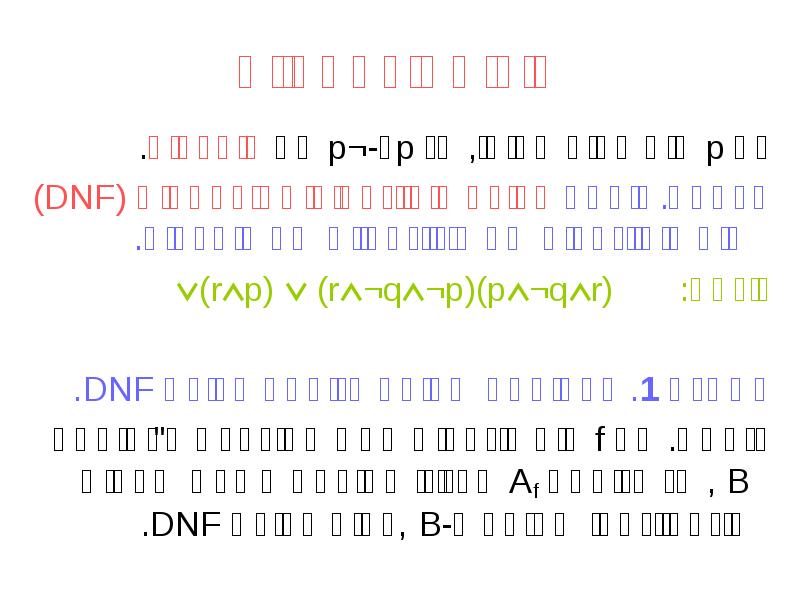
- 29. צורות נורמאליות אם p הוא פסוק אטומי, אז p ו-¬p הם
- 30. דואליות הגדרה: תהי A נוסחה שמכילהT , , , , ו-
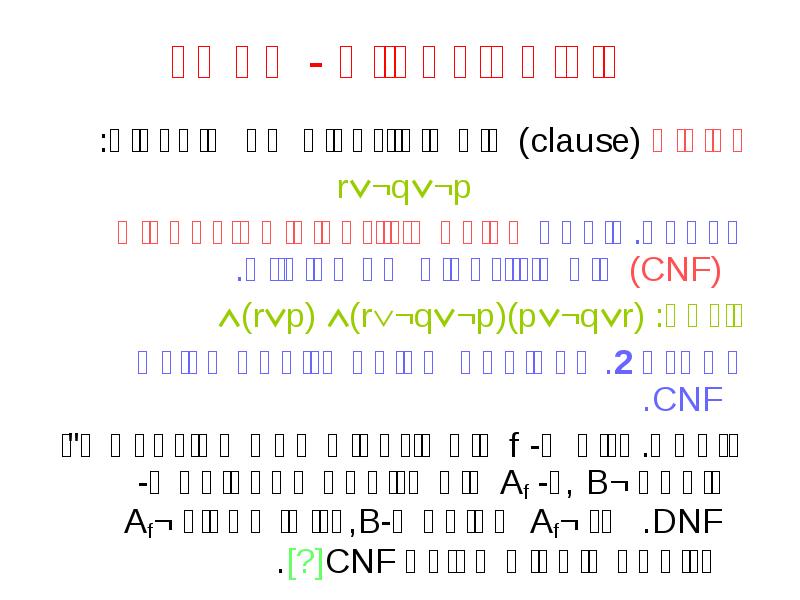
- 31. צורות נורמליות - המשך פסוקית (clause) היא דיסיונקציה של ליטרלים: r¬q¬p
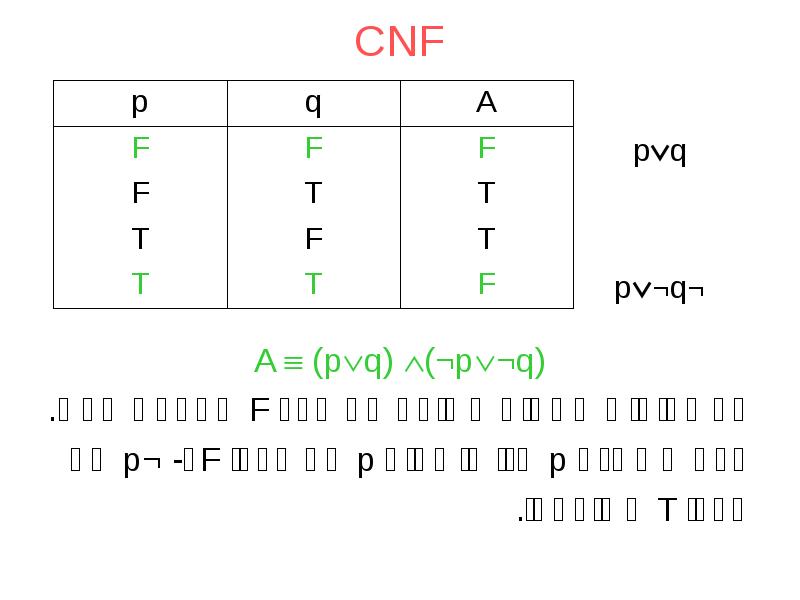
- 32. CNF A (pq) (¬p¬q) כל פסוקית מתאים לשורה עם ערך
- 33. אלגוריתמים לבניית DNF ו-CNF סילוק ו- ; הכנסת שלילה פנימה
- 34. פסוקיות הורן פסוקית הורן (Horn clause) היא פסוקית שמכילה לא יותר
- 35. אלגוריתם הכרעה לנוסחאות הורן אלגוריתם HORN להכרעת ספיקות: נסמן אטומים בנוסחת
- 36. משפט. אלגוריתם HORN מכריע בעיית ספיקות לנוסחאות הורן. משפט. אלגוריתם HORN
- 37. Скачать презентацию







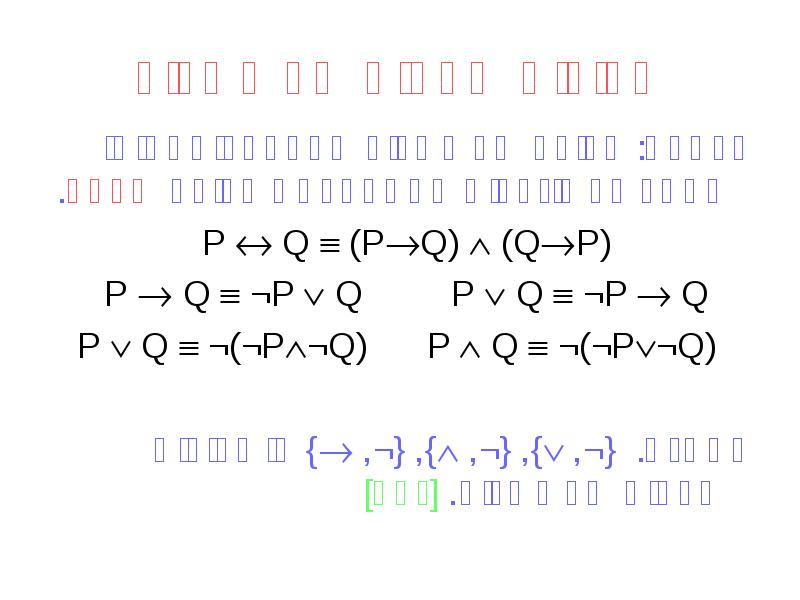





Слайды и текст этой презентации
Похожие презентации