Инженерные расчеты численными методами презентация
Содержание
- 2. Введение [1] В данном курсе под инженерными расчетами будем понимать расчеты,
- 3. Например, в геофизических методах при поиске нефти преобладает сейсморазведка, задачей которой
- 6. Погрешности [1] Приходится признать, что при измерении данных и при их
- 7. Случайные погрешности – возникают за счет случайных помех или ошибок человека,
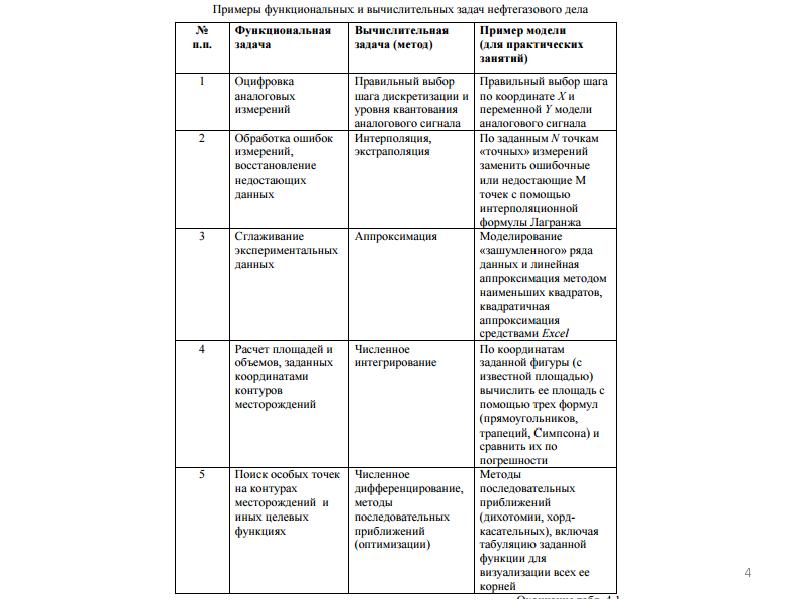
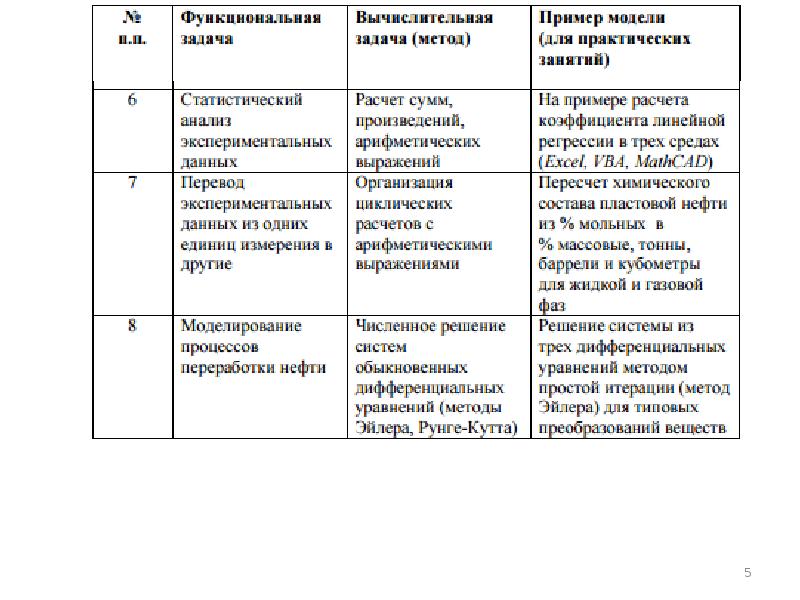
- 8. Виды численных методов 1. Анализ данных. Аппроксимация. Интерполяция. 2. Итерационные.
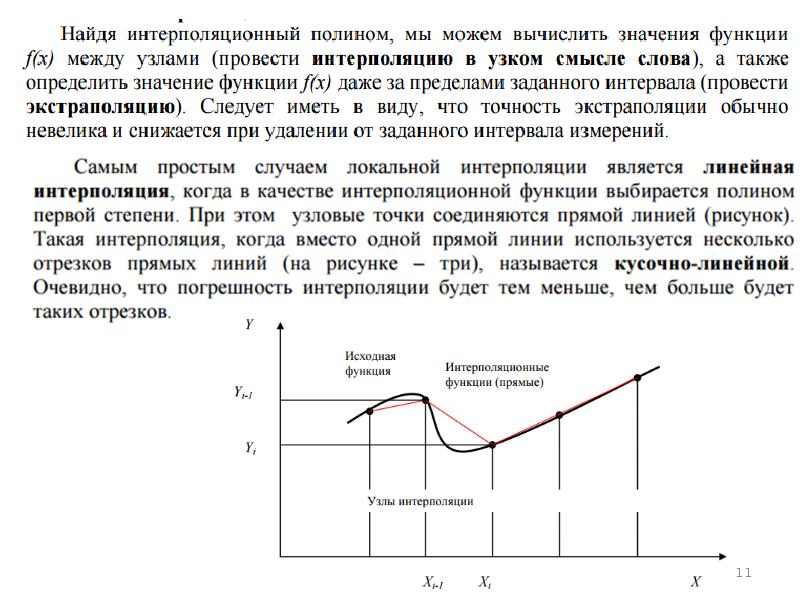
- 16. Рассмотрим применение различной интерполяции для анализа данных и прогнозирования Введение в
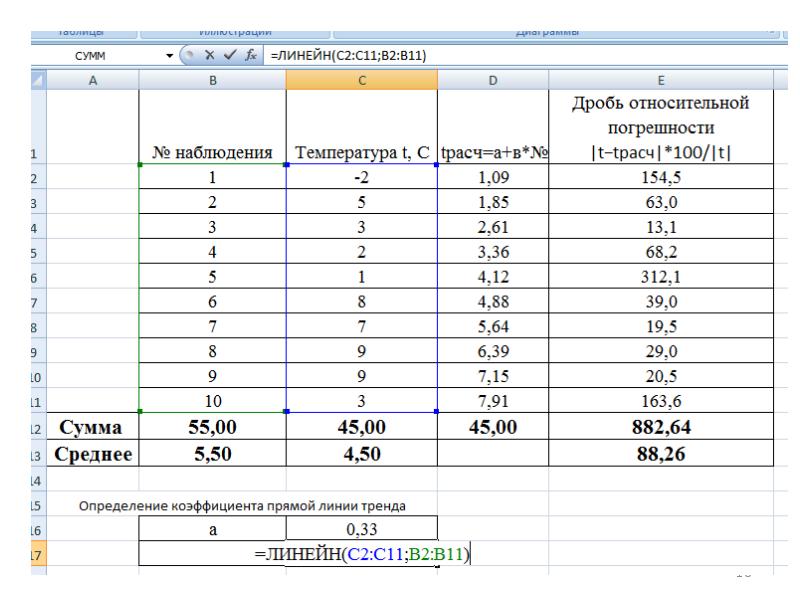
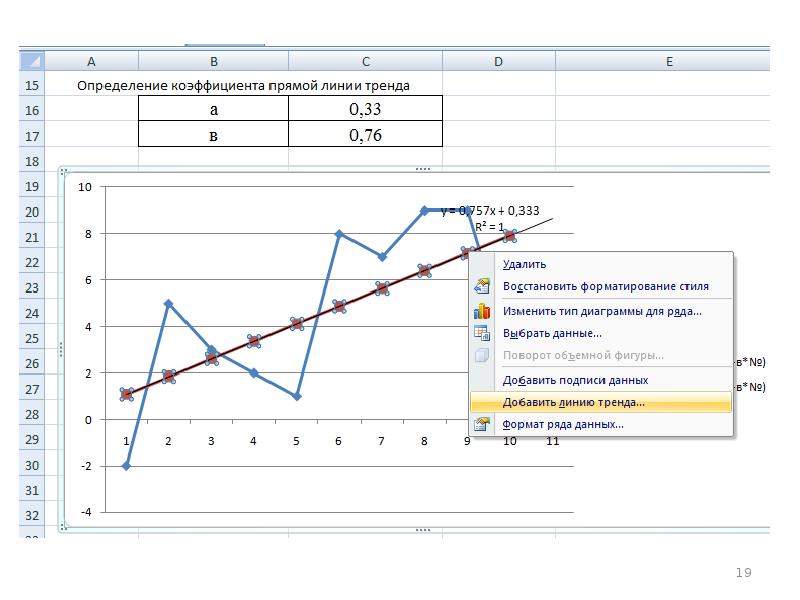
- 17. Для определения коэффициентов тренда (а и в) выполняют следующие действия:
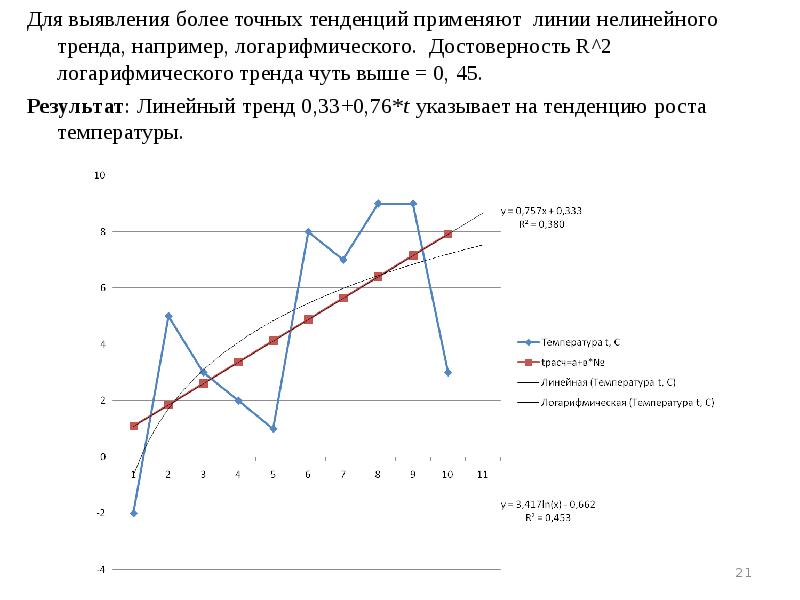
- 21. Для выявления более точных тенденций применяют линии нелинейного тренда, например, логарифмического.
- 22. Задание 1 Итак, ваше первое задание: определить линейный, полиномиальный и логарифмический
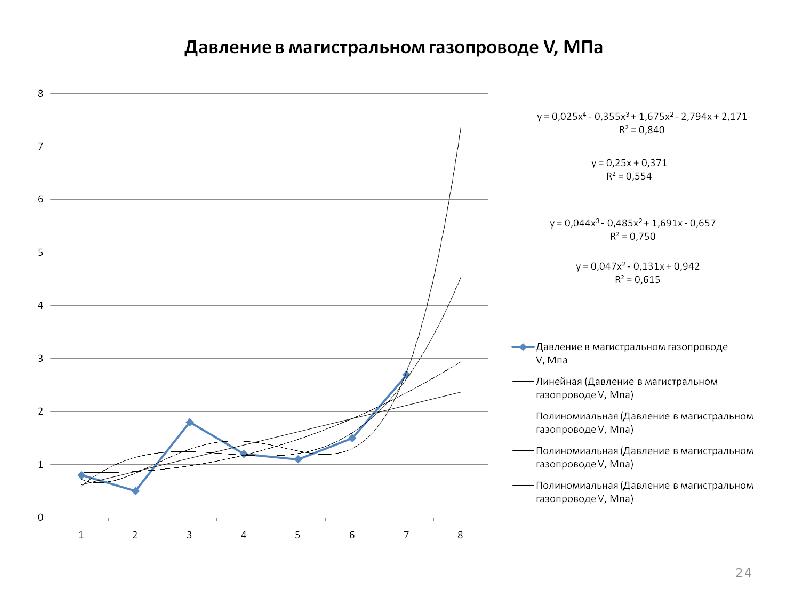
- 23. Линии тренда можно продлить на графике за пределы измеренных данных. Это
- 25. Как мы видим, в данном примере, степень достоверности полиномов повышается вместе
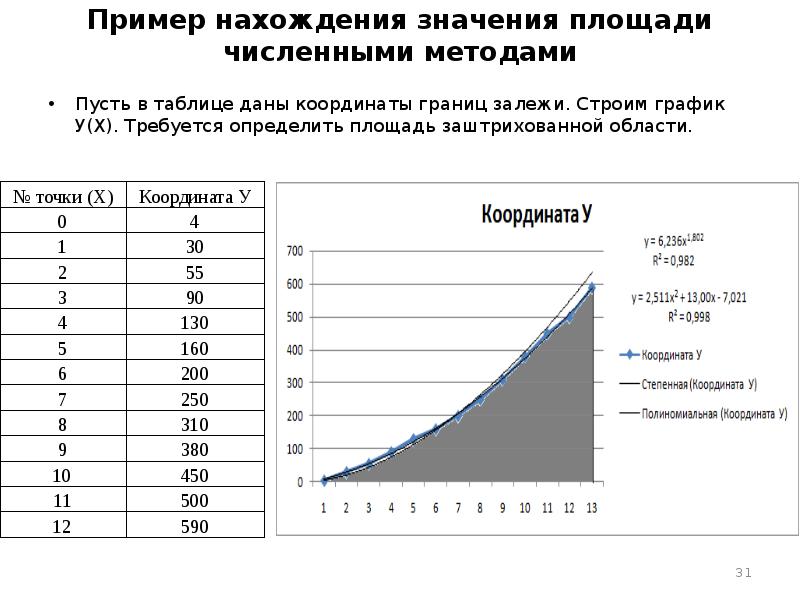
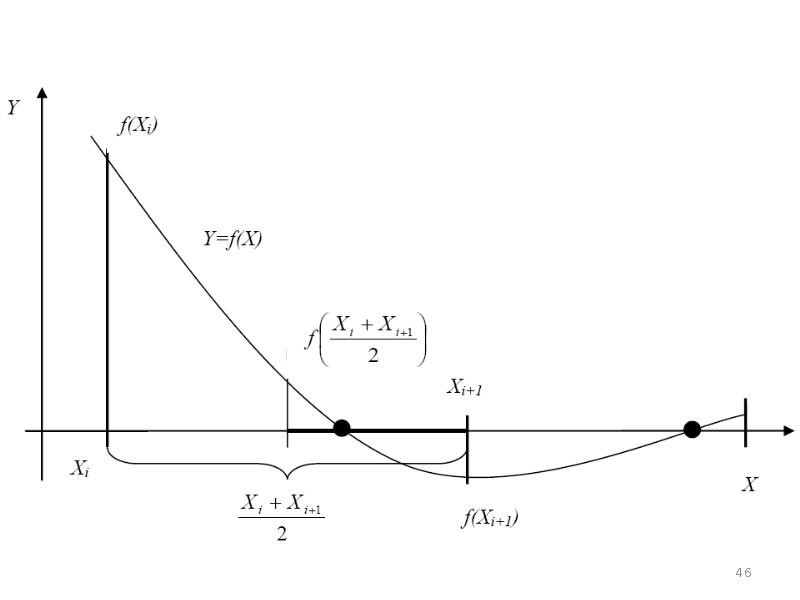
- 31. Пример нахождения значения площади численными методами Пусть в таблице даны координаты
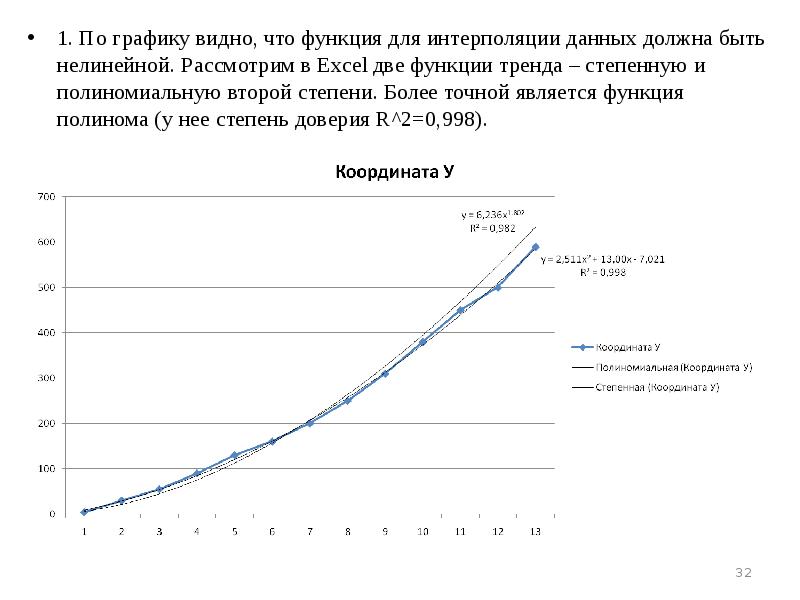
- 32. 1. По графику видно, что функция для интерполяции данных должна быть
- 33. 2. Но не забываем, что речь идет о приближенных численных методах,
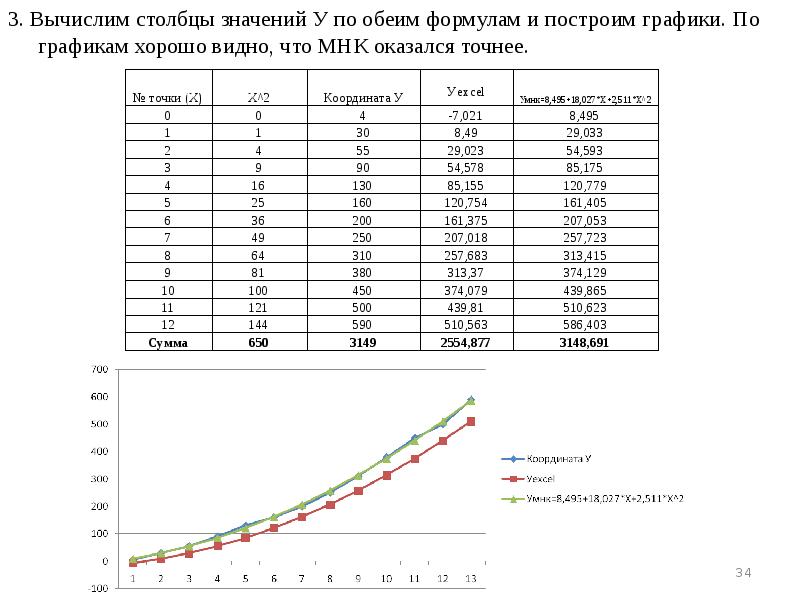
- 34. 3. Вычислим столбцы значений У по обеим формулам и построим графики.
- 35. 4. Вычислим в MathCAD/SMathStudio определенный интеграл от функции, полученной МНК.
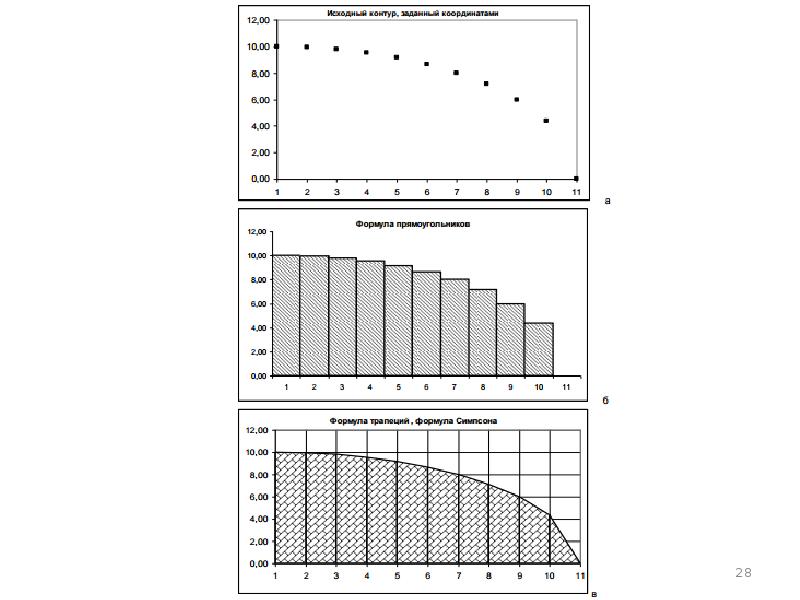
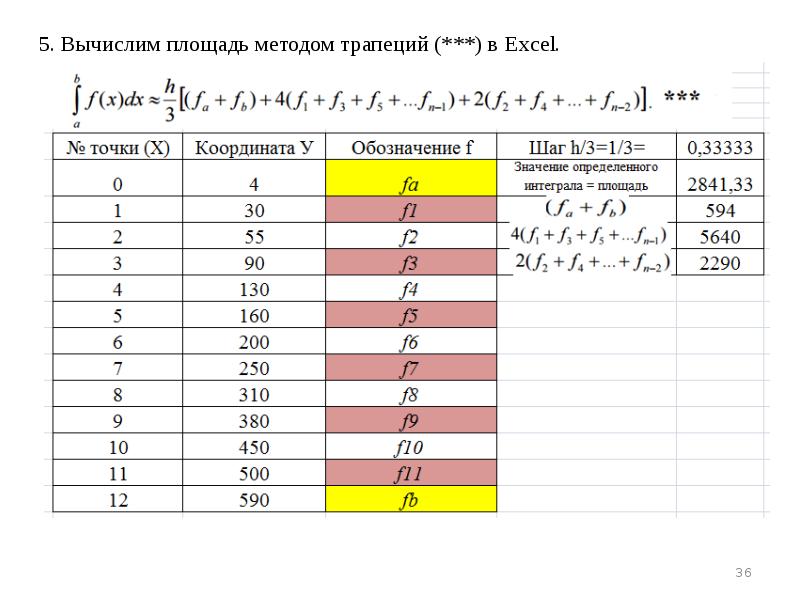
- 36. 5. Вычислим площадь методом трапеций (***) в Excel. 5. Вычислим площадь
- 37. 6. Как мы видим значение 2841,33 близко к эталонному 2846,22. 6.
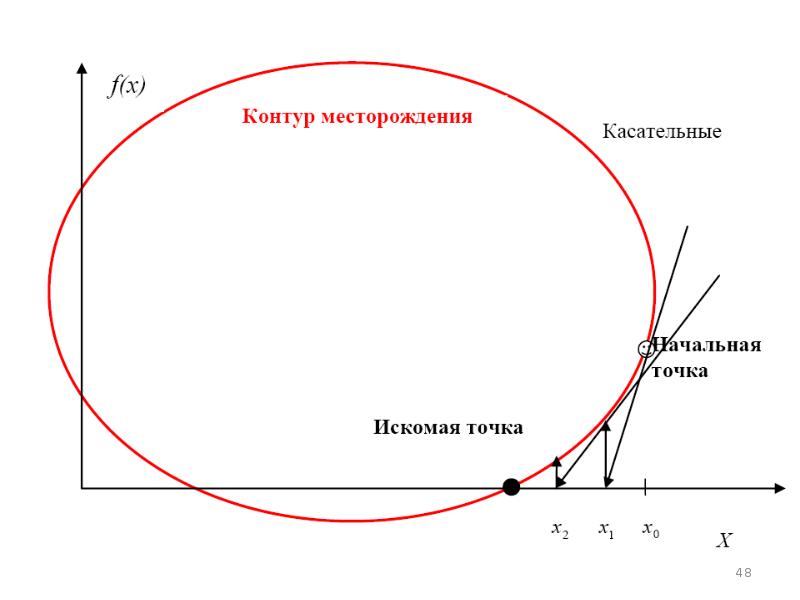
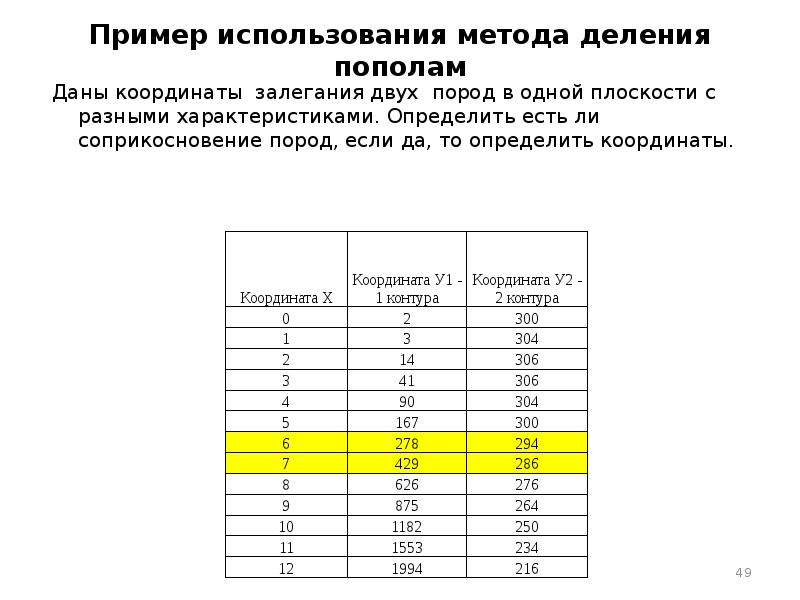
- 49. Пример использования метода деления пополам Даны координаты залегания двух пород в
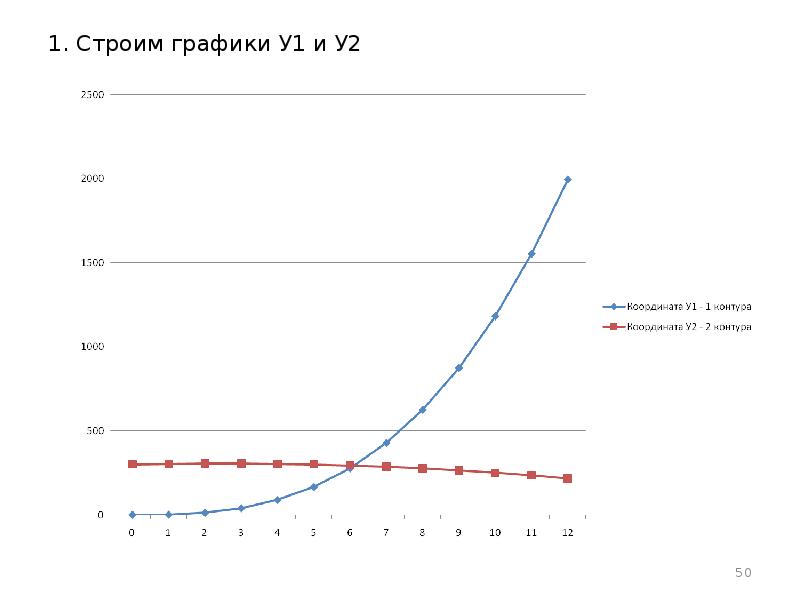
- 50. 1. Строим графики У1 и У2 1. Строим графики У1 и
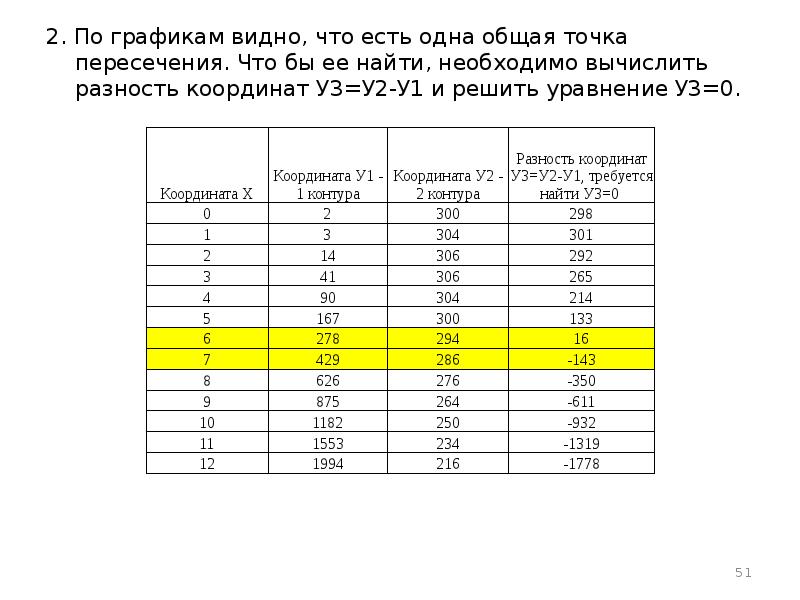
- 51. 2. По графикам видно, что есть одна общая точка пересечения. Что
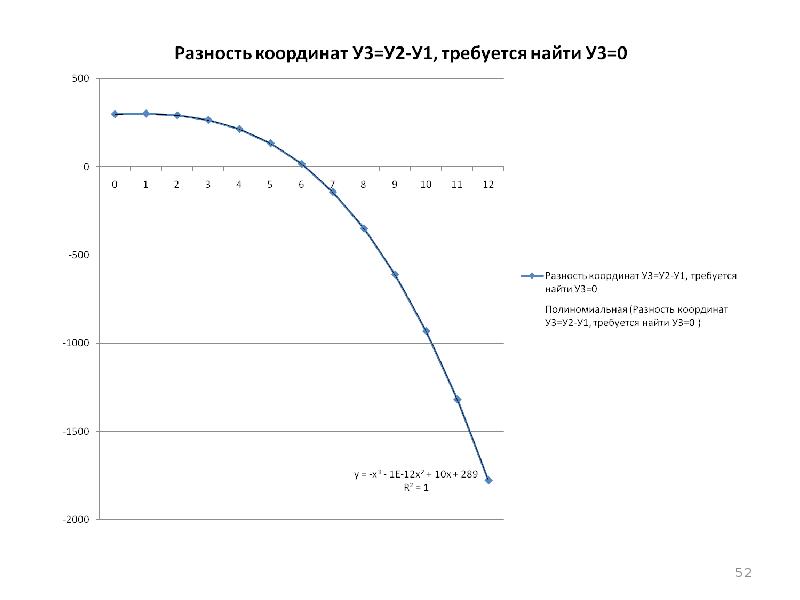
- 53. 3. По правилу дихотомии – корень У3=0 находится на том отрезке,
- 54. 5. Таким образом определена формула полинома третьей степени У3мнк=298+7*Х-3*Х^2-1*X^3. Вычислим столбец
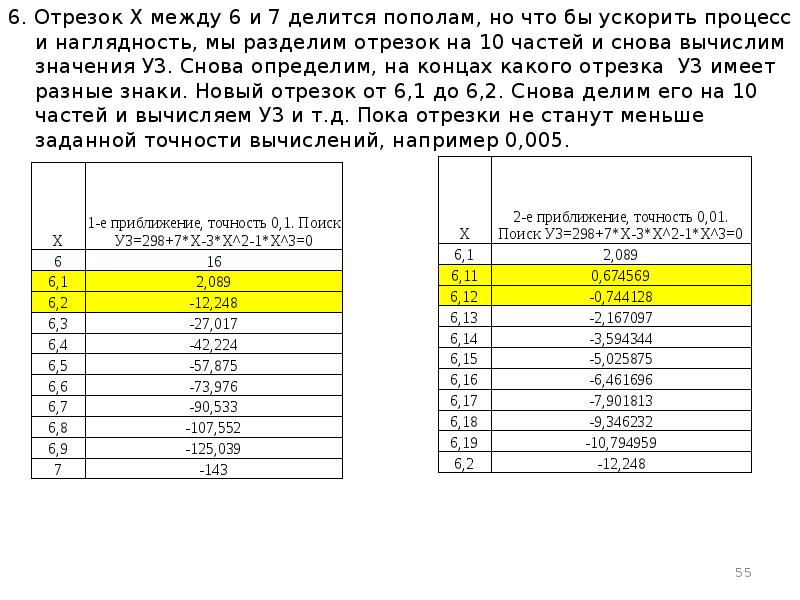
- 55. 6. Отрезок Х между 6 и 7 делится пополам, но что
- 56. Предварительный результат: Пласты У1 и У2 пересекаются в одной точке с
- 58. 7. Таким образом формула У2=300+5*Х-1*Х^2. 7. Таким образом формула У2=300+5*Х-1*Х^2. В
- 61. Список использованной литературы и интернет - источников 1. Введение в информатику/
- 62. Скачать презентацию

![Введение [1]
В данном курсе под инженерными расчетами будем понимать расчеты, Введение [1]
В данном курсе под инженерными расчетами будем понимать расчеты,](/documents_3/dceb6b1bd0324acdb4495eaabebd5567/img1.jpg)

![Погрешности [1]
Приходится признать, что при измерении данных и при их Погрешности [1]
Приходится признать, что при измерении данных и при их](/documents_3/dceb6b1bd0324acdb4495eaabebd5567/img5.jpg)






































Слайды и текст этой презентации
Скачать презентацию на тему Инженерные расчеты численными методами можно ниже:
Похожие презентации