Табличные распознаватели. Алгоритм Эрли. Алгоритм Кока—Янгера—Касами (Лекция 8) презентация
Содержание
- 2. Алгоритм Эрли Начальное состояние определяется как <S'→•#S#; 0>. На каждом
- 3. Завершатель. Этот оператор применяется к любой ситуации вида <А→α•; q> в
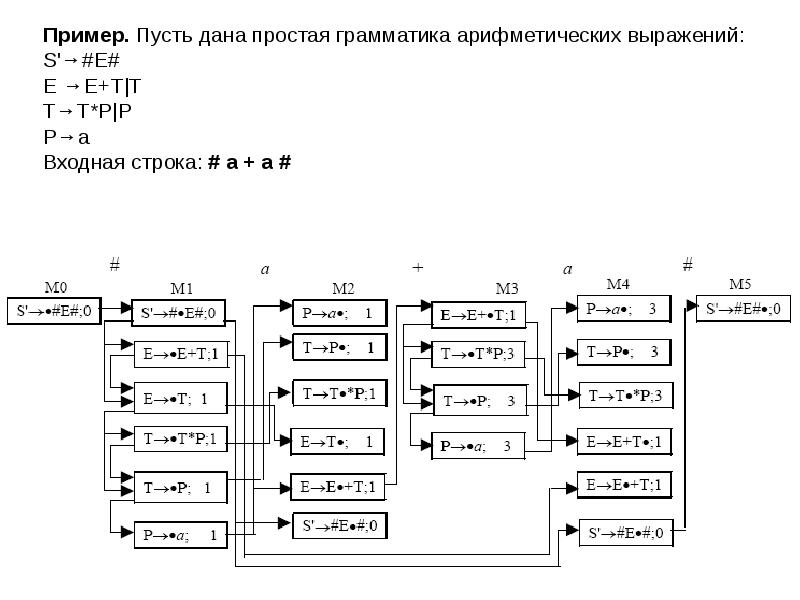
- 4. Пример. Пусть дана простая грамматика арифметических выражений: Пример. Пусть дана
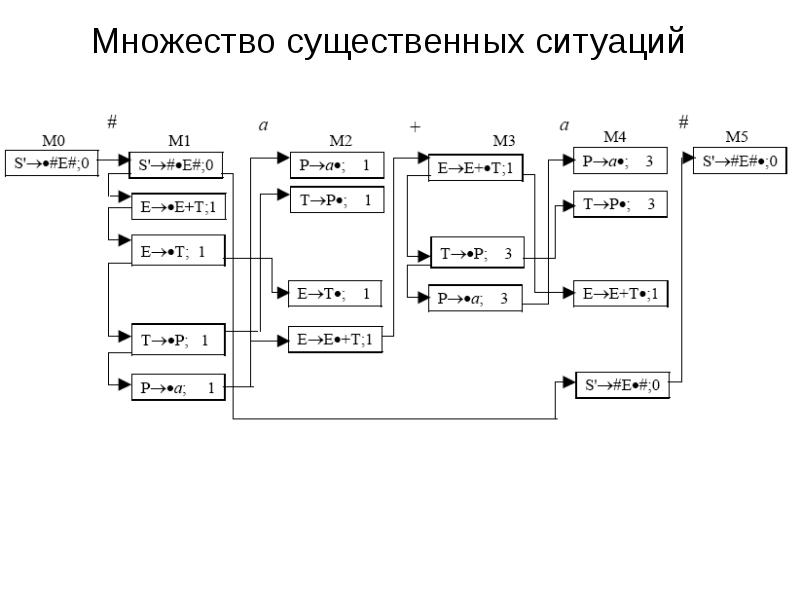
- 5. Множество существенных ситуаций Множество существенных ситуаций
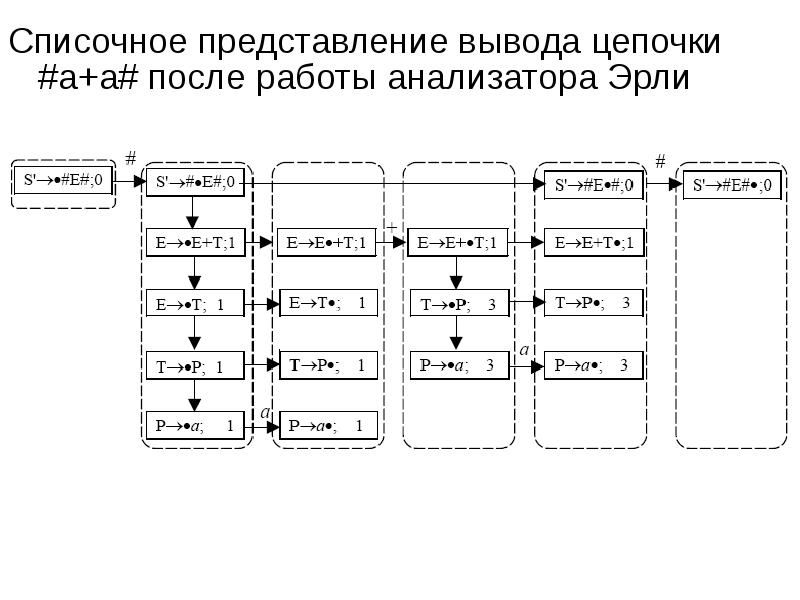
- 6. Списочное представление вывода цепочки #a+a# после работы анализатора Эрли Списочное
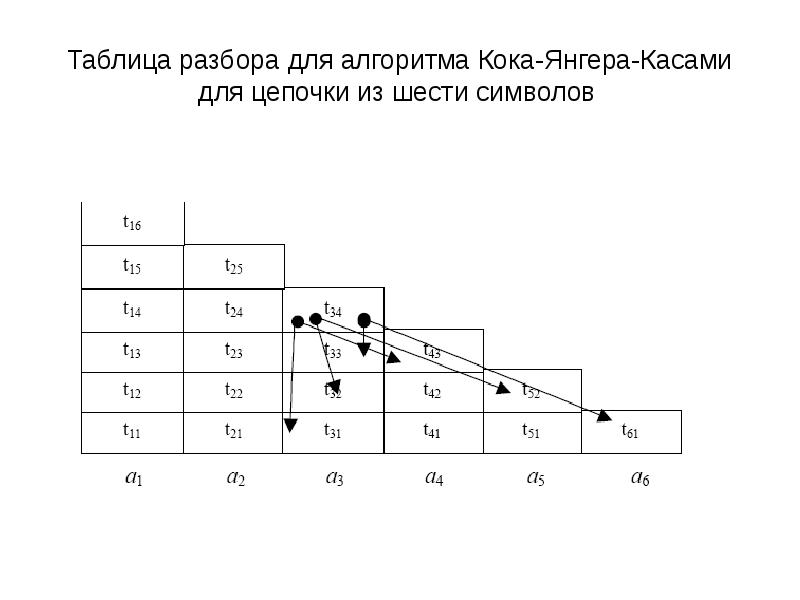
- 7. Алгоритм Кока-Янгера-Касами Суть алгоритма – в построении треугольной таблицы разбора
- 8. Таблица разбора для алгоритма Кока-Янгера-Касами для цепочки из шести символов
- 9. Пример. Проведем синтаксический анализ цепочки ( )( )( ) в двусмысленной
- 10. Цикл для i от 2 до n Цикл для i от
- 11. Второй шаг алгоритма Второй шаг алгоритма – это восстановление дерева вывода
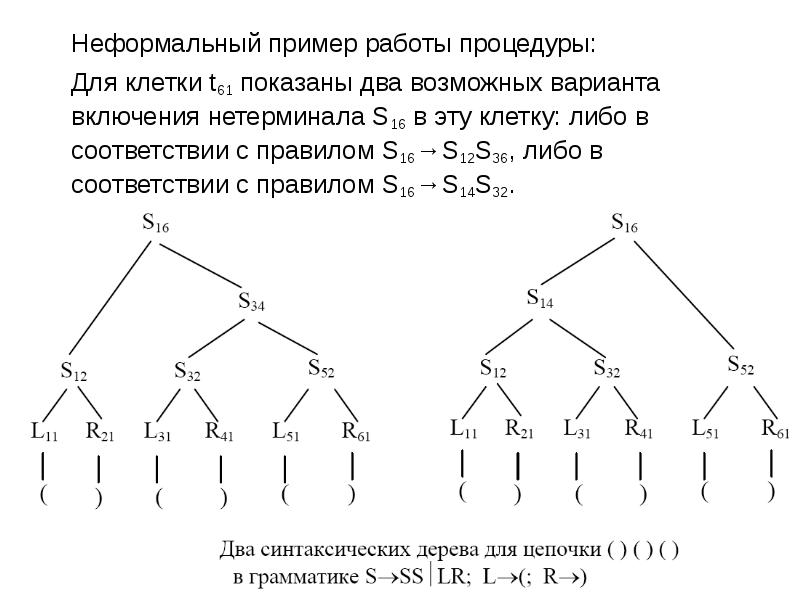
- 12. Неформальный пример работы процедуры: Неформальный пример работы процедуры: Для клетки t61
- 13. Скачать презентацию







Слайды и текст этой презентации
Скачать презентацию на тему Табличные распознаватели. Алгоритм Эрли. Алгоритм Кока—Янгера—Касами (Лекция 8) можно ниже:
Похожие презентации