Теория двойственности в линейном программировании презентация
Содержание
- 2. Требуется составить такой план выпуска продукции, при котором предприятие получает максимальную
- 3. a11x1 + a12x2 + … + a1nxn b1 a11x1 +
- 4. 1. цена единицы ресурса i - го вида (pi) не может
- 5. Покупающая организация заинтересована в том, чтобы затраты на все ресурсы в
- 6. f = b1y1 + b2y2 + … + bmym min
- 7. На изготовление единицы продукции j – го вида (j = 1,
- 8. 2. Симметричные и несимметричные двойственные задачи. 2. Симметричные и несимметричные двойственные
- 9. Две задачи линейного программирования, обладающие указанными свойствами, называются симметричными двойственными задачами.
- 10. 3. Первая основная теорема двойственности. Если одна из задач двойственной пары
- 11. 4.Решение симметричных двойственных задач. 4.Решение симметричных двойственных задач. При доказательстве первой
- 12. При решении исходной задачи, применяется алгоритм метода искусственного базиса, который является
- 13. Пример. Решить задачу линейного программирования Пример. Решить задачу линейного программирования F
- 14. Биекция в нашем случае приобретает вид: Биекция в нашем случае приобретает
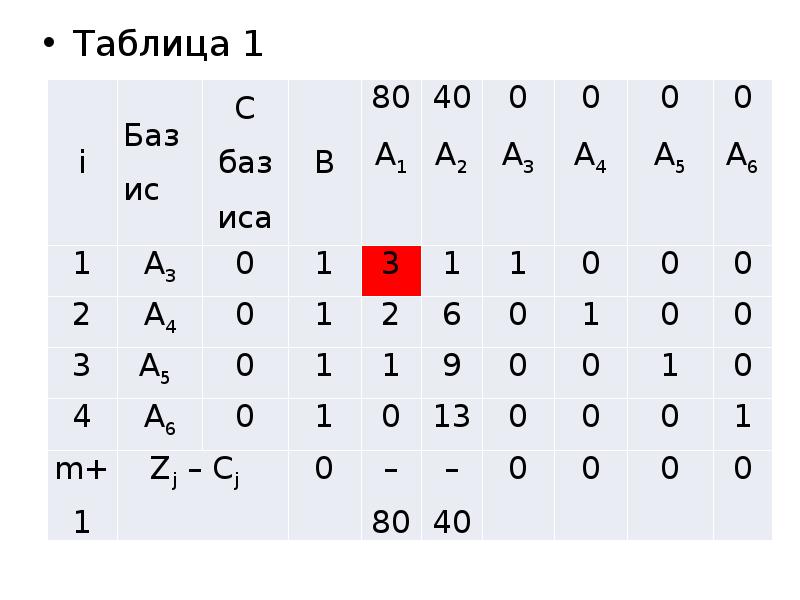
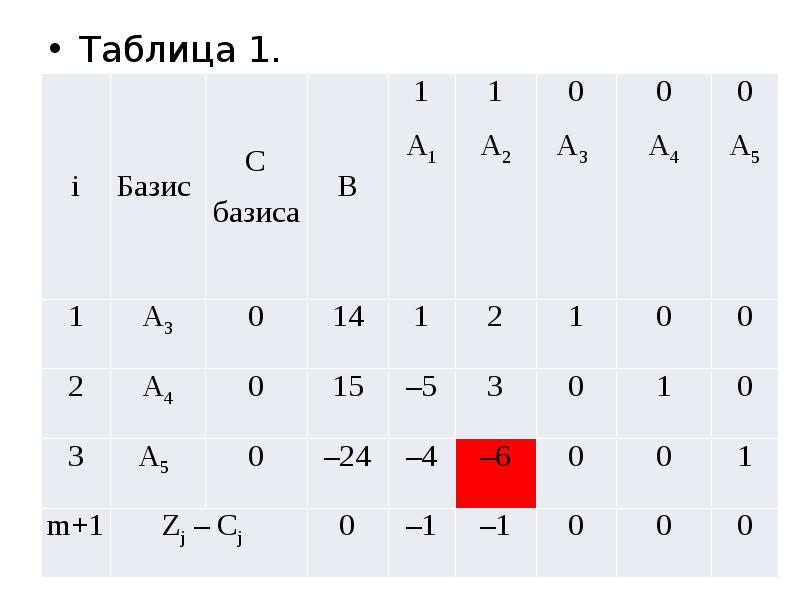
- 15. Таблица 1 Таблица 1
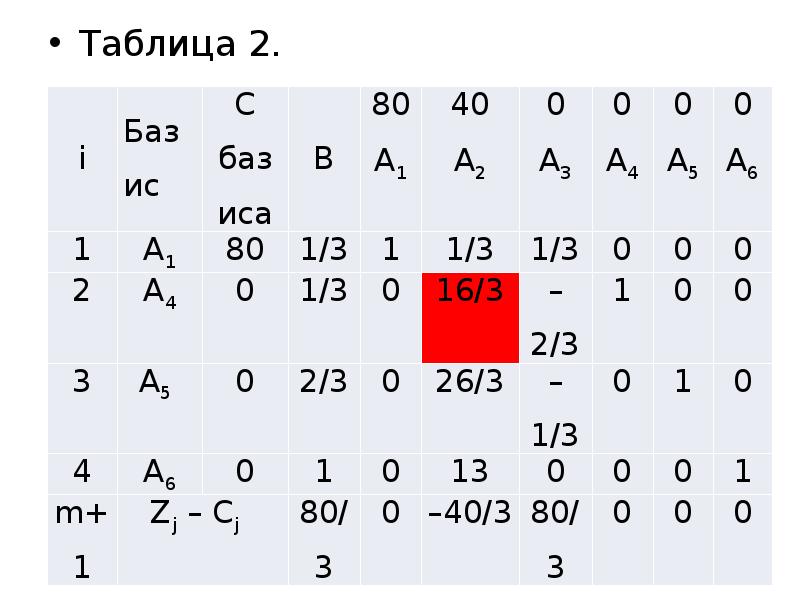
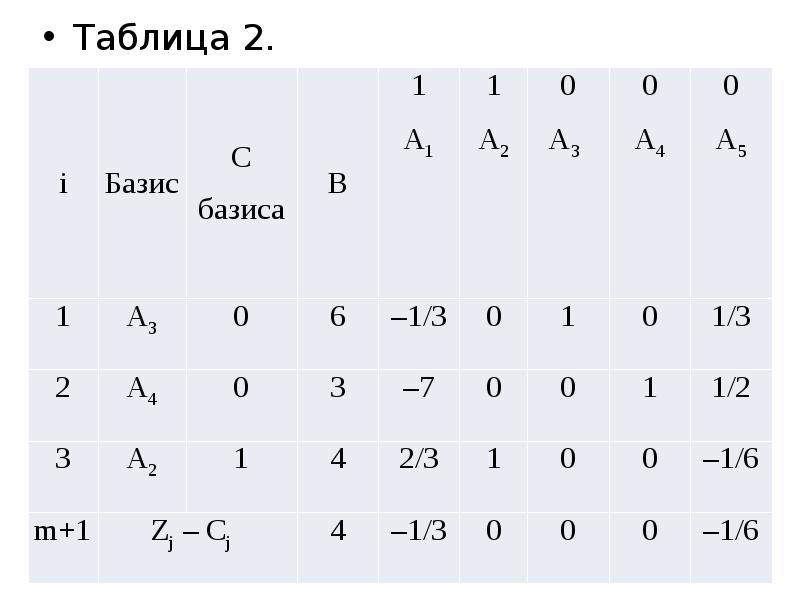
- 16. Таблица 2. Таблица 2.
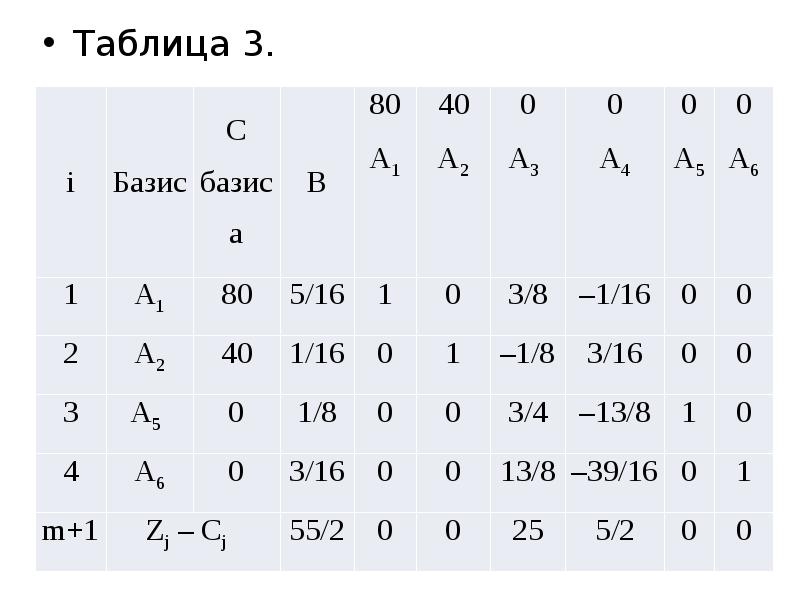
- 17. Таблица 3. Таблица 3.
- 18. Полученный план является оптимальным, т.к. среди оценок (m+1) –й строки нет
- 19. 5. Двойственный симплексный метод. 5. Двойственный симплексный метод. Для решения задачи
- 20. Если же некоторые akj < 0, то для столбцов, содержащих эти
- 21. Решить задачу линейного программирования двойственным симплексным методом: Решить задачу линейного программирования
- 22. Таблица 1. Таблица 1.
- 23. Таблица 2. Таблица 2.
- 24. 7. Вторая основная теорема двойственности и ее экономическое содержание. Для того
- 25. Скачать презентацию



















Слайды и текст этой презентации
Скачать презентацию на тему Теория двойственности в линейном программировании можно ниже:
Похожие презентации