Трехмерная графика в Matlab презентация

Трехмерная графика в Matlab

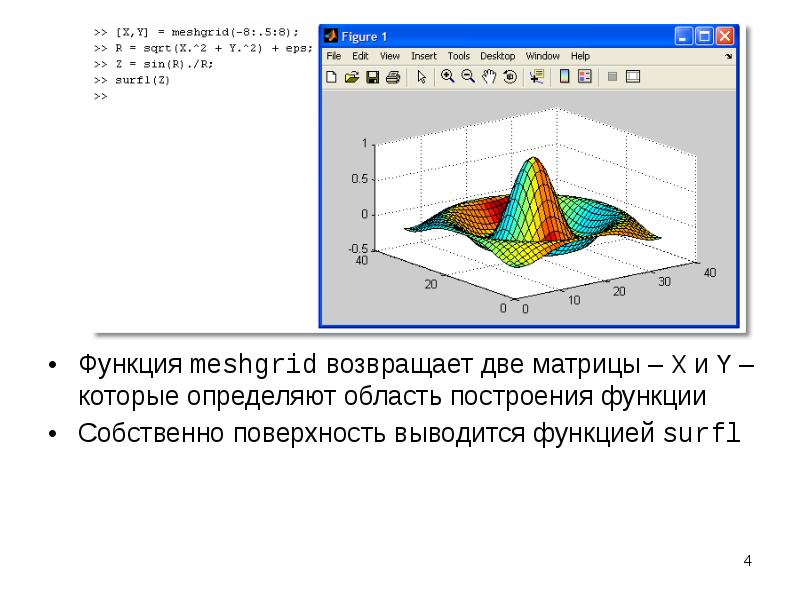
Построение 3D-поверхности Рассмотрим пример: построить поверхность f(x,y)=sin(r)/r, где r=sqrt(x2+y2)

Функция meshgrid возвращает две матрицы – X и Y – которые определяют область построения функции Функция meshgrid возвращает две матрицы – X и Y – которые определяют область построения функции Собственно поверхность выводится функцией surfl

Функция meshgrid Функция meshgrid служит для создания массивов данных для трехмерной графики.

Функция meshgrid записывается в следующих формах: [X,Y] = meshgrid(x) аналогична [X,Y] = meshgrid(x,x) возвращает трехмерные массивы [X,Y] = meshgrid(x,y) преобразует область, заданную векторами х и у, в массивы X и Y

Пример: [X,Y] = meshgrid(1:3,13:17) X = 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 Y = 13 13 13 14 14 14 15 15 15 16 16 16 17 17 17

Функции для построения поверхностей

Трехмерная графика. Трехмерная графика.

Команда plot3 plot3(X,Y,Z) – строит поверхность в виде линий, получаемых в сечении поверхности плоскостями, параллельными плоскости yOz. X, Y и Z – это матрицы: X,Y – задают узлы сетки, а матрица Z – значения по оси z в этих узлах.

Пример построения командой plot3 [X,Y]=meshgrid([-3:0.15:3]); Z=X.^2 + Y.^2; plot3(X,Y,Z);

plot3 (X, Y, Z, S) — обеспечивает построения с учетом спецификации стиля линий и точек S, соответствующей спецификации команды plot. plot3 (X, Y, Z, S) — обеспечивает построения с учетом спецификации стиля линий и точек S, соответствующей спецификации команды plot. plot3 может строить на одном рисунке графики нескольких функций z1(x1,y1), z2(x2, y2) и т. д. со спецификацией линий и маркеров каждой из них. plot3(x1,y1,z1,s1, х2,у2,z2,s2, хЗ,уЗ,z3,s3,...)

цвет стиль точек стиль линий цвет стиль точек стиль линий b синий . точка - сплошная g зеленый o кружок : пунктирная r красный x x-крестик -. штрихпунктирная c циан + плюс -- штрихами m фиолетовый * звездочка (none) без линий y желтый s квадрат k черный d кристалл w белый v треугольник (вниз) ^ треугольник (вверх) < треугольник (влево) > треугольник (вправо) p пятиугольник h шестиугольник

График поверхности, построенный кружками [X,Y]=meshgrid([-3:0.15:3]); Z=X.^2 + Y.^2; plot3(X,Y,Z,’o’);

[X,Y]=meshgrid([-3:0.15:3]); [X,Y]=meshgrid([-3:0.15:3]); Z=X.^2+Y.^2; plot3(X,Y,Z,'-r',Y,X,Z,'-b')

Сетчатые 3D-графики с окраской Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. В названии их команд присутствует слово mesh.

Команды mesh mesh – выводит в графическое окно сетчатую поверхность; meshc — помимо графика поверхности дает изображение ее проекции; meshz — строит поверхность в виде столбиков.

[X,Y]=meshgrid([-3:0.15:3]); [X,Y]=meshgrid([-3:0.15:3]); Z=X.^2+Y.^2; mesh(X,Y,Z);

Оформление графика поверхности Для удаления с поверхности линий, изображающих ребра, а также получения плавного перехода цветов на освещенной поверхности, используется команда shading interp Для получения информации о всех свойствах графического объекта, создаваемого функцией mesh, используется команда get:

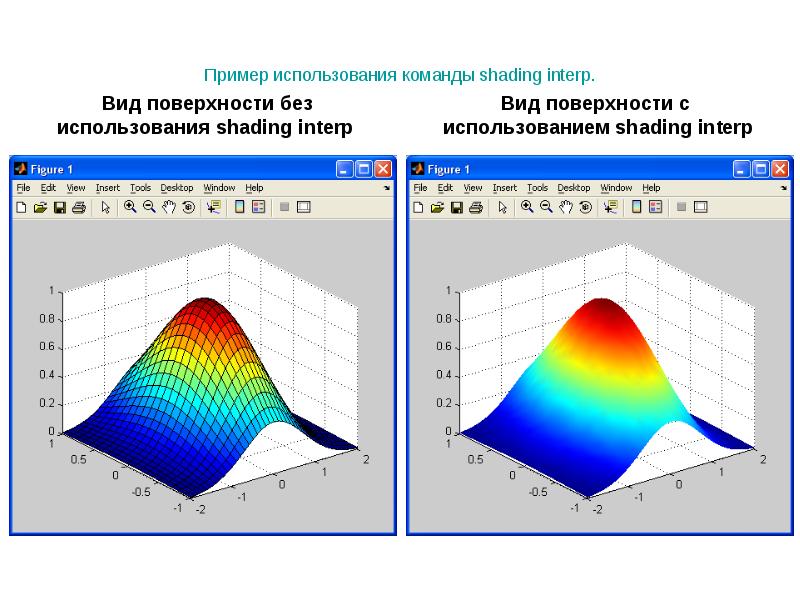
Пример использования команды shading interp.

[X,Y]=meshgrid([-3:0.15:3]); [X,Y]=meshgrid([-3:0.15:3]); Z=X.^2 + Y.^2; meshc(X,Y,Z);

Построение поверхности столбцами Использование суффикса z приводит к построению «графика с пьедесталом». Поверхность строится из многочисленных столбцов: meshz(...)

[X,Y]=meshgrid([-3:0.15:3]); [X,Y]=meshgrid([-3:0.15:3]); Z=X.^2 + Y.^2; meshz(X,Y,Z);

Для оформления трехмерных графиков можно использовать те же функции, что использовались при оформлении двумерных графиков функций, рассмотренных ранее, такие как: axis([ xmin, xmax, ymin, ymax, zmin, zmax ]), text, xlabel, ylabel, zlabel, title. С помощью функции subplot можно разместить в одном графическом окне несколько трехмерных графиков.

Построение поверхности с окраской Для построения поверхностей в виде сетчатых графиков, использующих функциональную закраску ячеек используются команды класса surf(…).

Команды surf surf — строит цветную параметрическую поверхность; surfc – обеспечивает дополнительное построение контурного графика проекции фигуры на опорную плоскость; surfl – строит график цветной поверхности с подсветкой от источника света;

[X,Y]=meshgrid([-3:0.1:3]); Z=sin(X)./(X.^2+Y.^2+0.3); surf(X,Y,Z); shading interp; colorbar;

Для повышения наглядности представления поверхностей можно использовать дополнительный график линий равного уровня, получаемый путем проецирования поверхности на опорную плоскость графика (под поверхностью). Для этого используется команда surfс: Для повышения наглядности представления поверхностей можно использовать дополнительный график линий равного уровня, получаемый путем проецирования поверхности на опорную плоскость графика (под поверхностью). Для этого используется команда surfс:

[X,Y]=meshgrid([-3:0.1:3]); [X,Y]=meshgrid([-3:0.1:3]); Z=sin(X)./(X.^2+Y.^2+0.3); surfc(X,Y,Z);

Контурные графики [X,Y]=meshgrid([-1:0.05:1]); Z=X.^2+Y.^2; levels=[0:0.1:0.5]; contour3(X,Y,Z,levels) colorbar Параметр levels может отсутствовать,тогда число линий уровня выбирается автоматически является просто значением является вектором значений

Контурные графики [X,Y]=meshgrid([-1:0.05:1]); Z=X.^2+Y.^2; levels=[0:0.01:0.5]; contour3(X,Y,Z,levels) colorbar

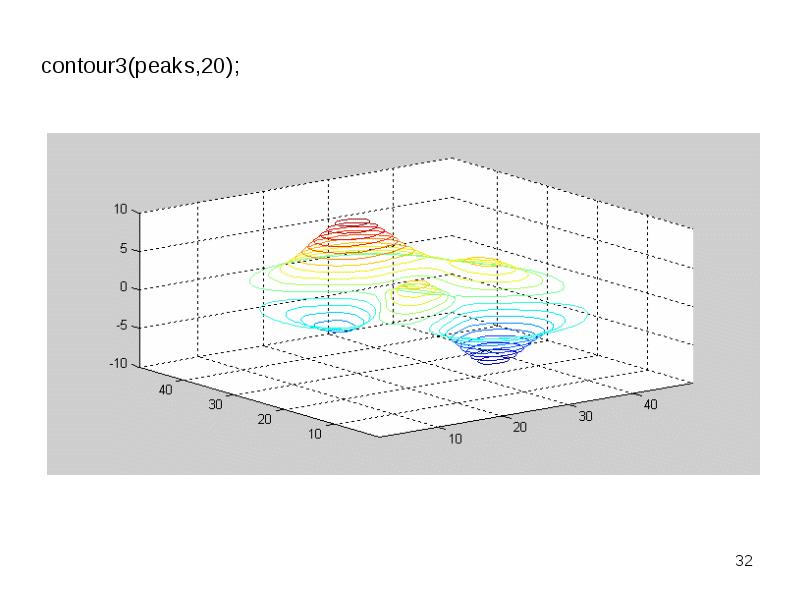
contour3(peaks,20); contour3(peaks,20);

Контурные графики Разновидность контурного графика contour(X,Y,Z) На плоскости xoy строятся линии уровня. Сам график поверхности не строится. В функции может стоять и 4-ый параметр, который указывает число линий уровня.

contour [X,Y]=meshgrid([-1:0.05:1]); Z=X.^2+Y.^2; [M,h]=contour(X,Y,Z); clabel(M,h)

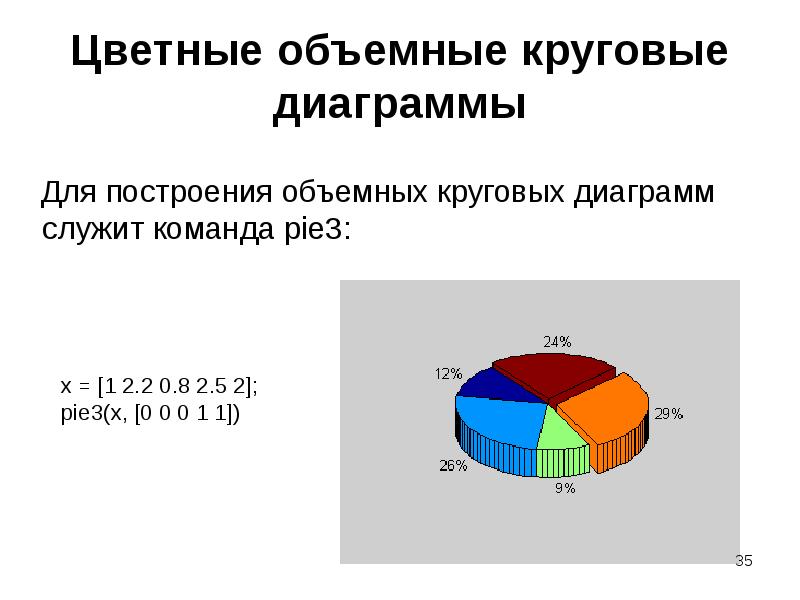
Цветные объемные круговые диаграммы Для построения объемных круговых диаграмм служит команда pie3:

MATLAB имеет несколько графических функций, возвращающих матричный образ поверхностей peaks – поверхность с рядом пиков и впадин cylinder – цилиндрическая поверхность ellipsoid – поверхность элипсоида sphere – сферическая поверхность

[X1,Y1,Z1]=cylinder(10,30); [X1,Y1,Z1]=cylinder(10,30); [X2,Y2,Z2]=sphere(30); [X3,Y3,Z3]=ellipsoid(0,0,0,3.9,3.9,2.25,30); subplot(2,2,1),surf(peaks); subplot(2,2,2),surf(X1,Y1,Z1,X1); subplot(2,2,3),surf(X2,Y2,Z2,X2); subplot(2,2,4),surf(X3,Y3,Z3,X3);

Вывод графиков в отдельные окна figure– окно становится текущим clf– очистка всего текущего окна cla – очистить оси, заголовки и названия осей In=figure - Создание указателя на графическое окно figure(In) – переход к нужному окну clf(In) – очистка нужного окна cla(In)

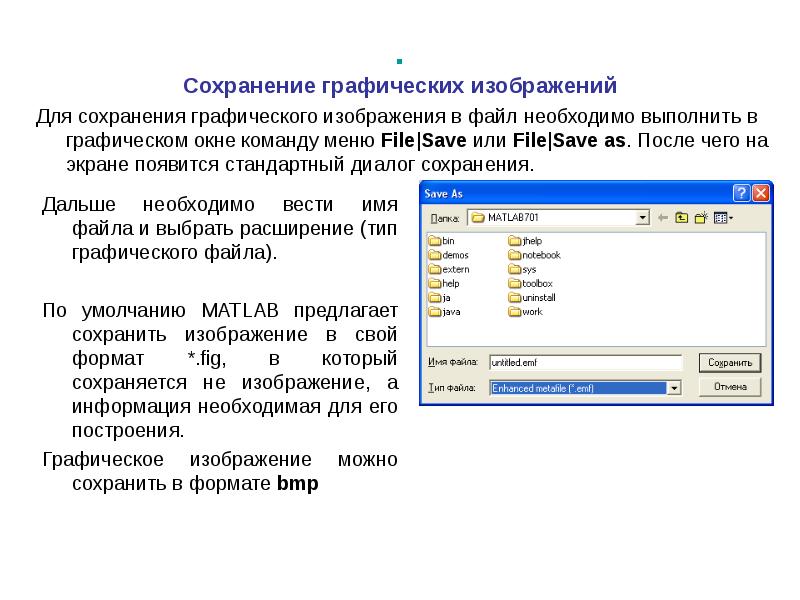
. Для сохранения графического изображения в файл необходимо выполнить в графическом окне команду меню File|Save или File|Save as. После чего на экране появится стандартный диалог сохранения.