Теорема Пифагора и её применение

Проблема исследования: Показать исторические истоки теоремы, умение применять полученные знания к решению прикладных задач.

Цель исследования: Обобщить и систематизировать знания по теме, учиться воспринимать материал в целостной системе различных предметов.

Задачи исследования: Расширение познавательного интереса к изучению геометрии. Разносторонний подход к изучению данной темы: как историки, лирики, теоретики и как практики.

теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Интересные факты Память . Афоризмы. Высказывания. Разное.

Афоризмы. «Не садись на хлебную меру» С равным достоинством относись к малым и великим мира сего. «Через весы не шагай» Не нарушай равновесия в природе. «Будь с тем, кто ношу взваливает, не будь с тем, кто  ношу  сваливает» Дружбу держи с кем мудрость постигаешь, чурайся глупцов, кто праздно время проводит. «Ласточек в доме не держи» Не замыкайся в себе, что знаешь, свободной судьбе предоставь. «Не ешь сердца» Не ничтожь  счастье других и не терзай себя душевными муками. «Корми петуха, но не приноси его в жертву, поскольку посвящен он Солнцу и Луне» Соразмерно чти и храни вожака и правителя, но не поступай вероломно, не предавай. «Меру во всем соблюдай и дела свои  во время делай» «Начало – пол-целого дела»

Изречения Пифагора

Разное. Пифагор первым определил и изучил взаимосвязь музыки и математики. Пифагор рассматривал геометрию не как практическую и прикладную дисциплину, а как логическую науку. Система морально-этических правил, завещанная Пифагором, была собрана в своеобразный моральный кодекс пифагорейцев «Золотые стихи». Во Франции и некоторых областях Германии в Средневековье теорему Пифагора называли «Мостом слов», а у математиков арабского Востока – «Теоремой невесты».

Не алгебраические доказательства теоремы: Простейшее доказательство. Древнекитайское доказательство. Древнеиндийское доказательство. Доказательство Евклида.

. "Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах." Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треуголь­ников, чтобы убедиться в справедливости теоремы. Например, для ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.

. Древнекитайское доказательство. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла тематика в девяти книгах» — главное из сохранившихся математико - астрономических сочинений в книге «Математики» помещен чертеж , доказывающий теорему Пифагора.

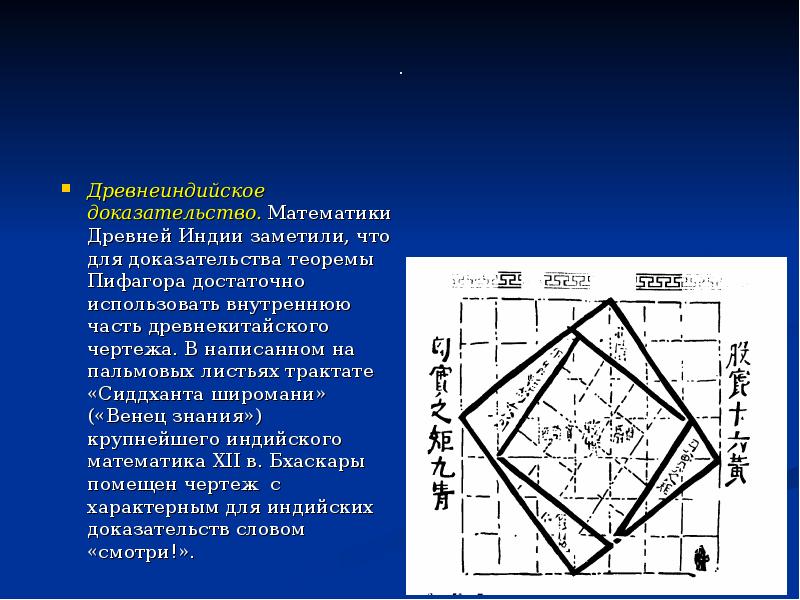
. Древнеиндийское доказательство. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж с характерным для индийских доказательств словом «смотри!».

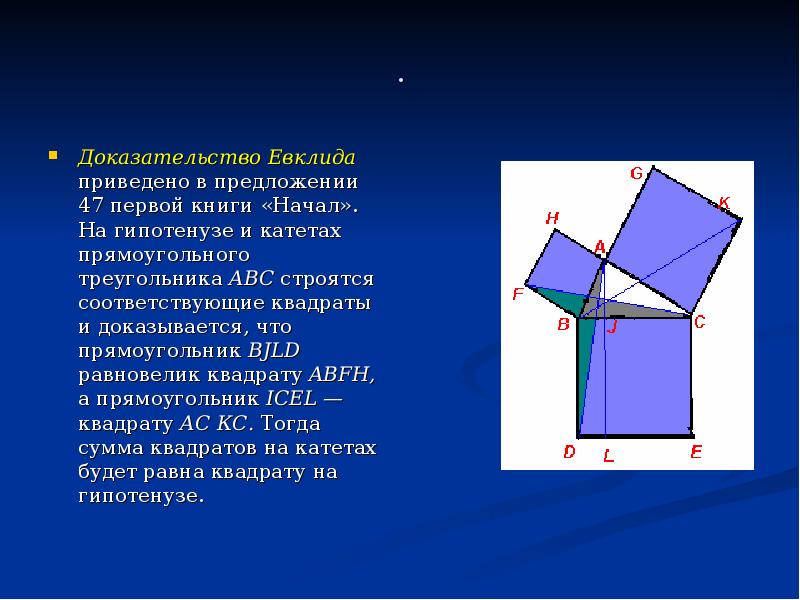
. Доказательство Евклида приведено в предложении 47 первой книги «Начал». На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL — квадрату АС КС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе.

Лирики о теореме Пифагора . теореме Пифагора посвятил свои стихи немецкий писатель А.Шамиссо

Задачи по планиметрии с практическим применением 12 апреля 1961 года Ю.А. Гагарин на космическом корабле “Восток” был поднят над землёй на максимальную высоту 327 километров. На каком расстоянии от корабля находились в это время наиболее удалённые от него и видимые космонавтом участки поверхности Земли? (Радиус Земли ≈6400 км).

. От пристани одновременно отплыли два корабля:один на юг, со скоростью 16 морских миль в час, а другой на запад, со скоростью 12морских миль в час. Какое расстояние будет между кораблями через 2,5 часа(1 морская миля равна 1,85 км)

. «ИСТОРИЧЕСКИЕ ЗАДАЧИ» Задача индийского математика XII века Бхаскары .

Задача из китайской «Математики в девяти книгах» .

Задача из учебника «Арифметика» Леонтия Магницкого .

. .

Заключение В заключении еще раз хочется сказать о важности теоремы. Значение ее состоит прежде всего в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако хочется надеется, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней.