Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лек презентация

Лекция 3 Постановка задачи. Применение интерполяции Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена Интерполяционный многочлен Лагранжа. Схема Эйткена

Задача аппроксимации Задача аппроксимации состоит в приближенной замене функции f(x), заданной таблично, на некоторую функцию ϕ(х) так, чтобы отклонение ϕ(х) от f(x) в некоторой области удовлетворяло заданному условию. Функция ϕ(х) называется аппроксимирующей функцией. В качестве аппроксимирующей функции часто используют алгебраический многочлен вида: ϕn(x) = a0 + a1x + a2x2 + … + anxn В этом случае говорят о параболической аппроксимации. Интерполяция является важным частным случаем аппроксимации.

Постановка задачи интерполяции Пусть функция y = f(x) задана таблицей значений в n+1 точке: так, что y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn). Требуется найти функцию F(x), приближающую функцию f(x) (f(x) = F(x) + R(x), где R(x) – погрешность интерполяции), совпадающую с функцией f(x) в точках xi (i=0, 1, 2, …n). Функция f(x) называется интерполируемой, F(x) – интерполирующей, точки xi (i=0, 1, 2, …n) – узлами интерполяции.

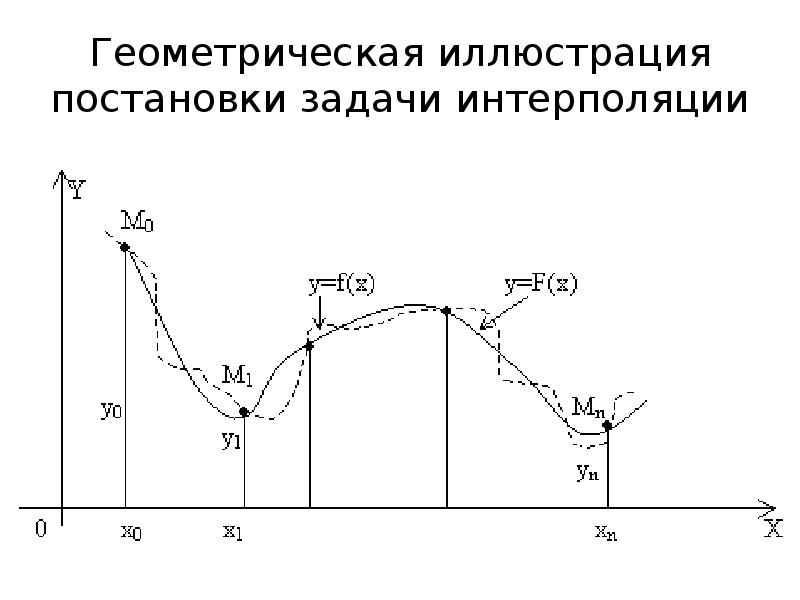
Геометрическая иллюстрация постановки задачи интерполяции

Применение интерполяции 1) интерполяция используется в тех случаях, когда интерполируемая функция известна лишь при некоторых дискретных значениях аргумента xi, а требуется получить ее приближенные значения в других точках x≠ xi: если f(xi) – результаты эксперимента (измерений); если f(xi) – результаты сложных вычислений на компьютере, например, результаты имитационного моделирования; если f(xi) – табличные значения некоторой элементарной или специальной функции, а требуется получить таблицу с меньшим шагом или значение функции при x≠ xi.

Применение интерполяции 2) интерполяция используется при решении ряда других задач вычислительной математики: приближенное нахождение корня уравнения f(x) = 0 методом обратной интерполяции; численное дифференцирование и интегрирование функции f(x); приближенное определение экстремума функции f(x).

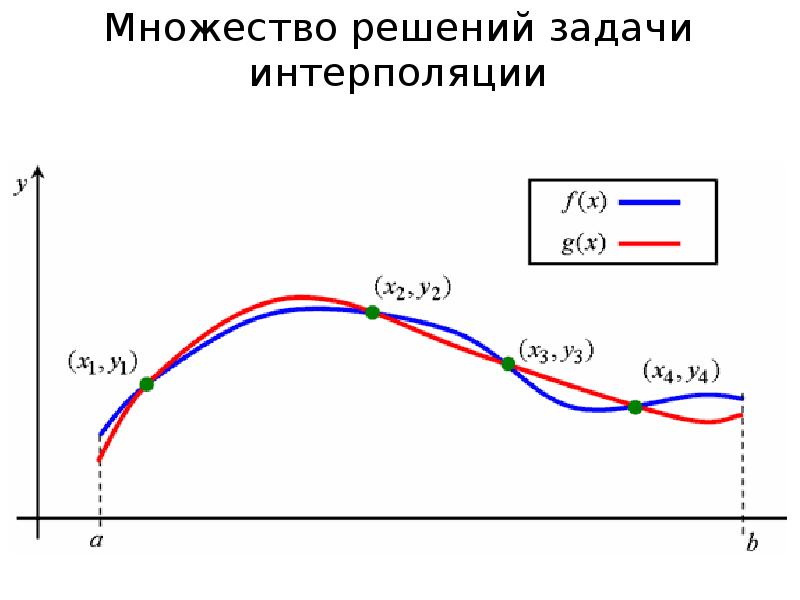
Множество решений задачи интерполяции

Виды интерполяции

Постановка задачи параболической интерполяции Функция y = f(x) задана таблицей значений в n+1 точке:   y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).   Требуется найти многочлен Pn(x) степени n, значения которого   Pn(xi) = f(xi), i=0, 1, 2, … n.

Единственность интерполяционного многочлена

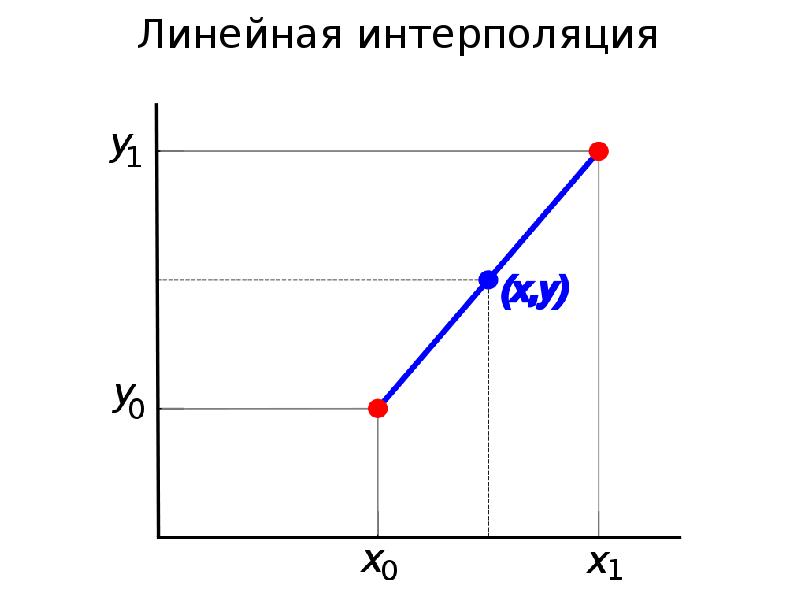
Линейная интерполяция

Пример построения интерполяционного многочлена непосредственным решением СЛУ

Интерполяционная формула Лагранжа

Интерполяционная формула Лагранжа

Интерполяционная формула Лагранжа Полученная формула называется интерполяционным многочленом Лагранжа. Несмотря на некоторую громоздкость, одним из преимуществ формулы Лагранжа является возможность ее записи непосредственно по заданной таблице значений функции. При этом следует учитывать следующие правила: формула содержит столько слагаемых, сколько узлов в таблице; каждое слагаемое – это произведение дробного коэффициента на соответствующее значение yi; числитель коэффициента при yi содержит произведение разностей х со всеми узлами кроме xi, а знаменатель полностью повторяет числитель при подстановке х = xi.

Формулы Лагранжа для линейной и квадратичной интерполяции

Пример использования формулы Лагранжа

Интерполяционная схема Эйткена

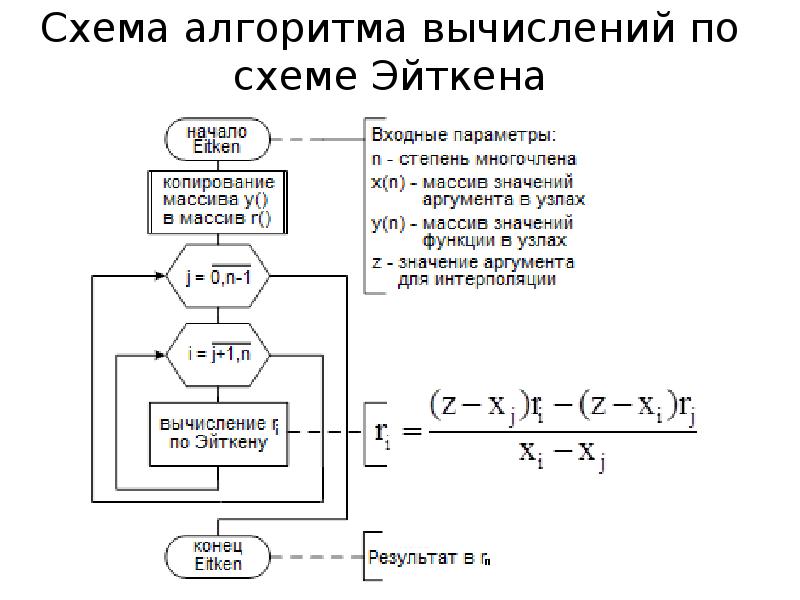
Схема алгоритма вычислений по схеме Эйткена