Функция y = cos x. Ее свойства и график

Функция y = cos x Ее свойства и график

Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения функции и аргумента; Изменение свойств функции y = cos x в зависимости от изменения функции и аргумента; Примеры построения графиков функций путем анализа изменения их свойств.

Построение графика Функция y = cos x определена на всей числовой прямой и множеством ее значений является отрезок -1; 1. Следовательно, график этой функции расположен в полосе между прямыми у = -1 и у = 1.

Как использовать периодичность и четность при построении Так как функция периодическая с периодом 2, то достаточно построить ее график на каком – нибудь промежутке длиной 2, например на отрезке -  х  ; тогда на промежутках, получаемых сдвигами выбранного отрезка на 2n, nZ, график будет таким – же.

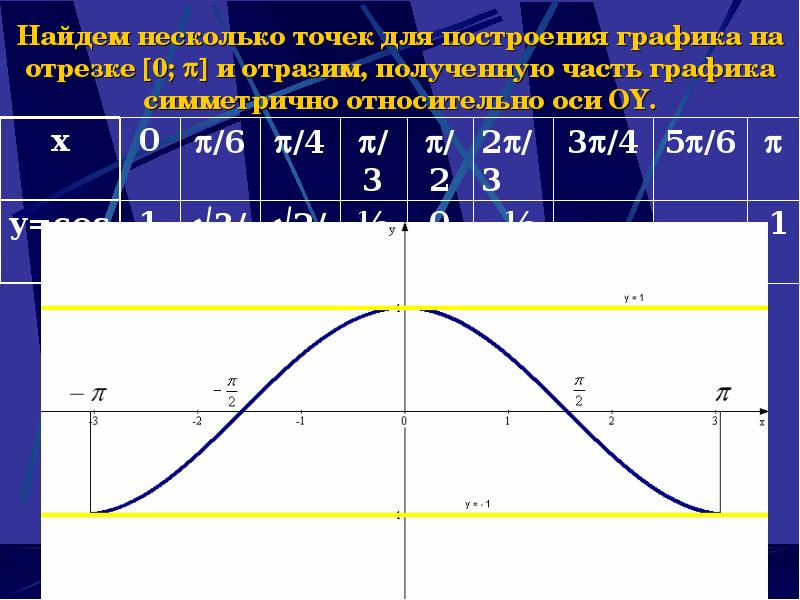
Найдем несколько точек для построения графика на отрезке 0;  и отразим, полученную часть графика симметрично относительно оси OY.

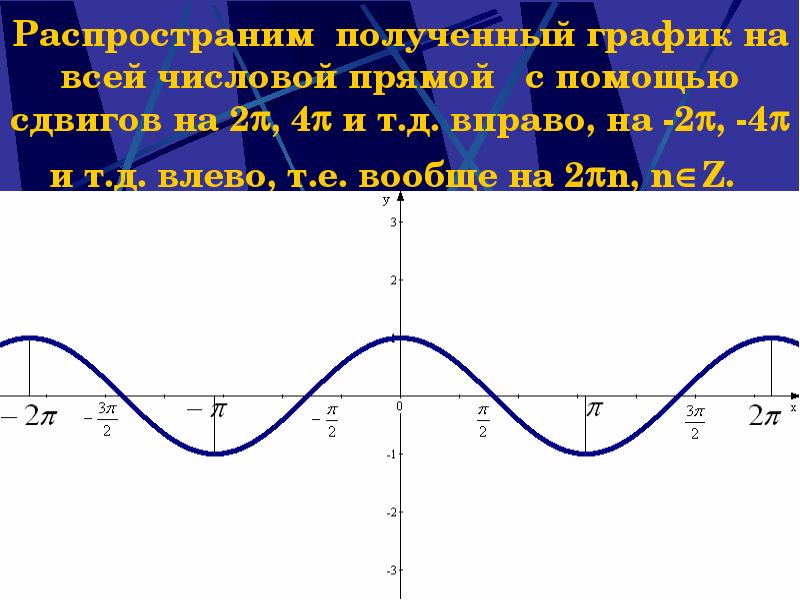
Распространим полученный график на всей числовой прямой с помощью сдвигов на 2, 4 и т.д. вправо, на -2, -4 и т.д. влево, т.е. вообще на 2n, nZ.

Итак, график функции y = cos x построен геометрически на всей числовой прямой, начиная с построения его части на отрезке 0; . Поэтому свойства функции y = cos x можно получить , опираясь на свойства этой функции на отрезке 0; . Например, функция y = cos x возрастает на отрезке -; 0, так как она убывает на отрезке 0;  и является четной. Перечислим основные свойства функции y = cos x.

Для этого нужно вспомнить Как найти область определения и множество значений тригонометрических функций; Какие функции называются периодическими и как найти период функции; Какие функции называются четными (нечетными); Когда функция возрастает (убывает); Как найти нули функции; Как определить на каких промежутках функция принимает положительные (отрицательные) значения; Как определить когда функция принимает наибольшее (наименьшее) значения.

Область определения Каждому действительному числу х соответствует единственная точка единичной окружности, получаемая поворотом точки 1; 0 на угол х радиан. Для этого угла определены sin x и cos x. Тем самым каждому действительному числу х поставлены в соответствие числа sin x и cos x, т.е. на множестве R всех действительных чисел определены функции y = sin x и y = cos x. Таким образом, областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.

Множество значений Чтобы найти множество значений функции y = cos x, нужно выяснить, какие значения может принимать y при различных значениях х, т.е. установить, для каких значений у есть такие значения х, при которых cos x = y. Известно, что уравнение cos x = a имеет корни, если |a|  1, и не имеет корней, если |a| > 1. Следовательно множеством значений функции y = cos x является отрезок –1  у  1.

Периодичность Функция y = f (x) называется периодической, если существует такое число Т  0, что для любого х из ее области определения выполняется равенство f (x – T) = f (x) = f (x + T). Число Т называется периодом функции. Известно, что для любого значения х верны равенства sin(x + 2)=sin x, cos(x + 2)= cos x. Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на 2. Такие функции называются периодическими с периодом 2.

Четность, нечетность Функция y = f (x) называется четной, если для каждого значения х из ее области определения выполняется равенство f (-x) = f (x), график симметричен относительно оси ординат. Функция y = f (x) называется нечетной, если для каждого значения х из ее области определения выполняется равенство f (-x) = -f (x), график симметричен относительно начала координат.

Возрастание, убывание Функция y = f(x) называется возрастающей, если наибольшему (наименьшему) значению функции соответствует наибольшее (наименьшее) значение аргумента. Т.е. если у1 > y2 (y1 < y2), то x1 > x2 (x1 < x2). Функция y = f(x) называется убывающей, если наибольшему (наименьшему) значению функции соответствует наименьшее (наибольшее) значение аргумента. Т.е. если у1 > y2 (y1 < y2), то x1 < x2 (x1 > x2).

Нули функции, положительные и отрицательные значения, наименьшее и наибольшее значения. Для того чтобы определить когда функция y = cos x принимает значения, равные: нулю; положительные; отрицательные; наименьшее; наибольшее,

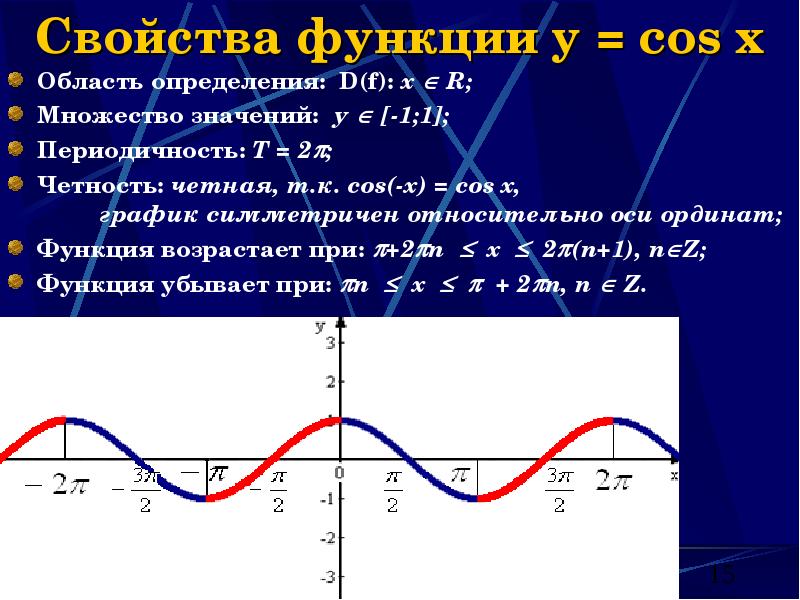
Свойства функции y = cos x Область определения: D(f): х  R; Множество значений: у  [-1;1]; Периодичность: Т = 2; Четность: четная, т.к. cos(-x) = cos x, график симметричен относительно оси ординат; Функция возрастает при: +2n  x  2(n+1), nZ; Функция убывает при: n  x   + 2n, n  Z.

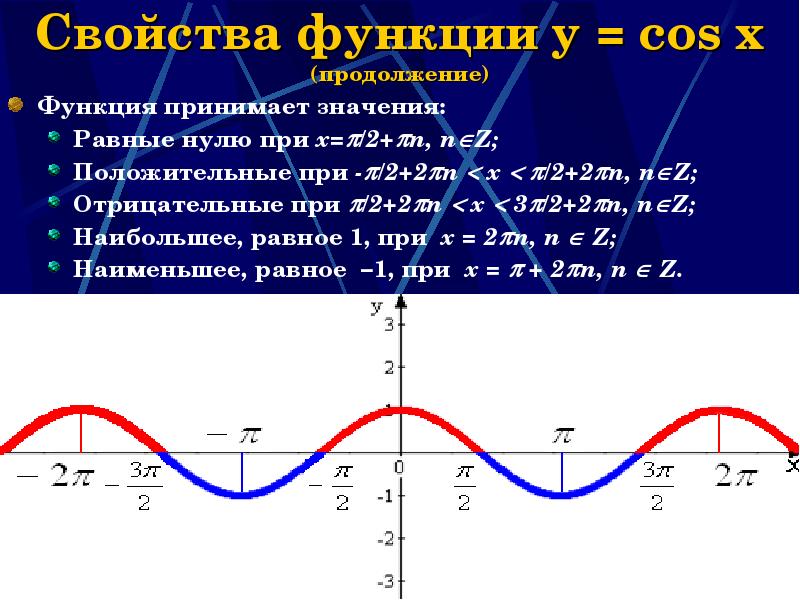
Свойства функции y = cos x (продолжение) Функция принимает значения: Равные нулю при х=/2+n, nZ; Положительные при -/2+2n  x  /2+2n, nZ; Отрицательные при /2+2n  x  3/2+2n, nZ; Наибольшее, равное 1, при x = 2n, n  Z; Наименьшее, равное –1, при x =  + 2n, n  Z.

Преобразование графика функции y = cos x Изменение функции y = cos x + A y = k · cos x y = - cos x y = cos x 

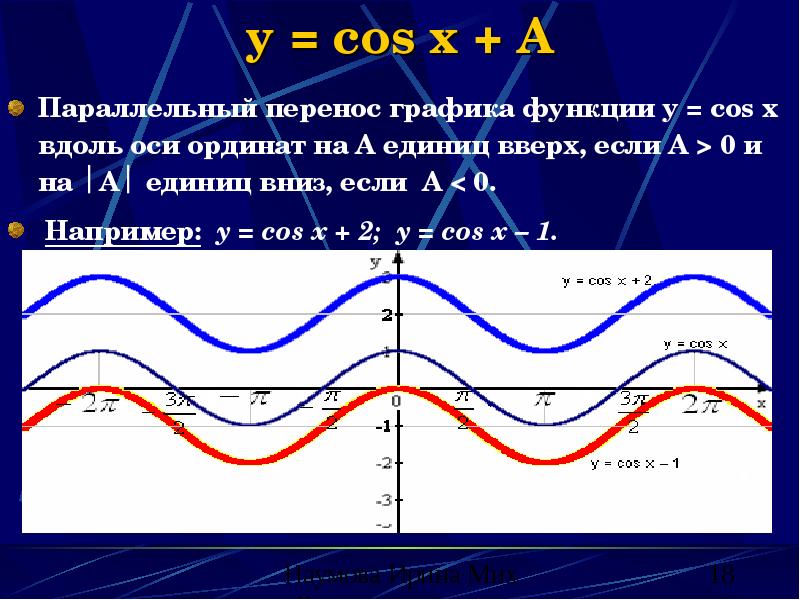
y = cos x + A Параллельный перенос графика функции у = соs x вдоль оси ординат на А единиц вверх, если А > 0 и на А  единиц вниз, если А < 0. Например: y = cos x + 2; y = cos x – 1.

y = cos x + A (свойства) Изменяются множество значений функции; наибольшее (наименьшее) значения; нули функции; промежутки положительных (отрицательных) значений. Например: y = cos x + 2. E (f): cos x + 2 = a  cos x = a – 2, т.к. – 1  y  1, то –1  а – 2  1  1  а  3, т.е. y  1; 3. Нули функции: cos x + 2 = 0  cos x = -2 данное уравнение не имеет корней т.к. |-2|  1  график данной функции не пересекает ось абсцисс. f (x) > 0: при любом значении х. f (x) < 0: нет. y (наиб) = 3, при: x = 2n, n  Z (т.к. cos x + 2 = 3  cos x = 1  x = 2n, n Z). y (наим) = 1, при: x =  + 2n, n Z (т.к. cos x + 2 = 1  cos x = - 1  x =  + 2n, n  Z).

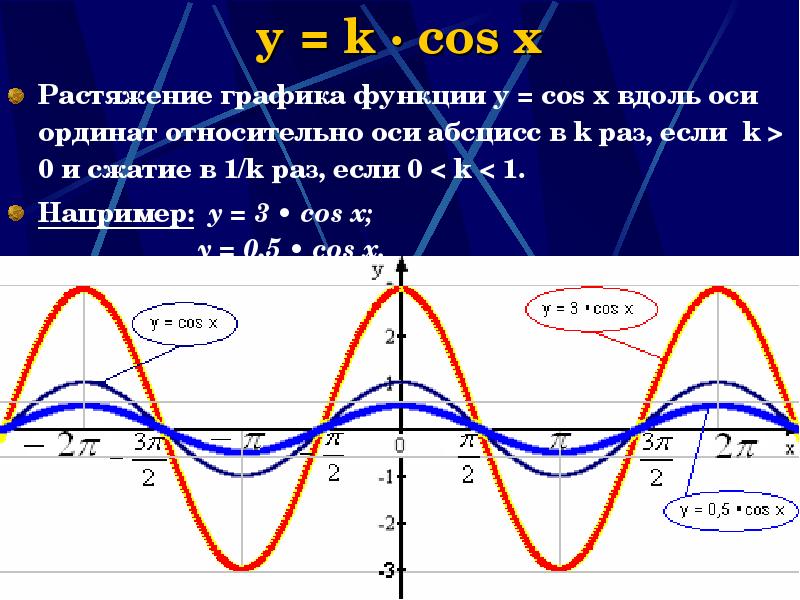
y = k · cos x Растяжение графика функции у = соs x вдоль оси ординат относительно оси абсцисс в k раз, если k > 0 и сжатие в 1/k раз, если 0 < k < 1. Например: y = 3 • cos x; y = 0,5 • cos x.

y = k · cos x (свойства) Изменяется множество значений функции; наибольшее (наименьшее) значения. Например: y = 3 • cos x E (f): 3•cos x = a  cos x = a/3, т.к. – 1  y  1, то - 1  a/3  1  - 3  a  3, т.е. y  -3; 3. Функция принимает наибольшее значение, равное 3, при: x = 2n, n  Z (т.к. 3cos x = 3  cos x = 1  x = 2n, n  Z). Функция принимает наименьшее значение, равное – 3, при: x =  + 2n, n  Z (т.к. 3cos x = - 3  cos x = - 1  x =  + 2n, n  Z).

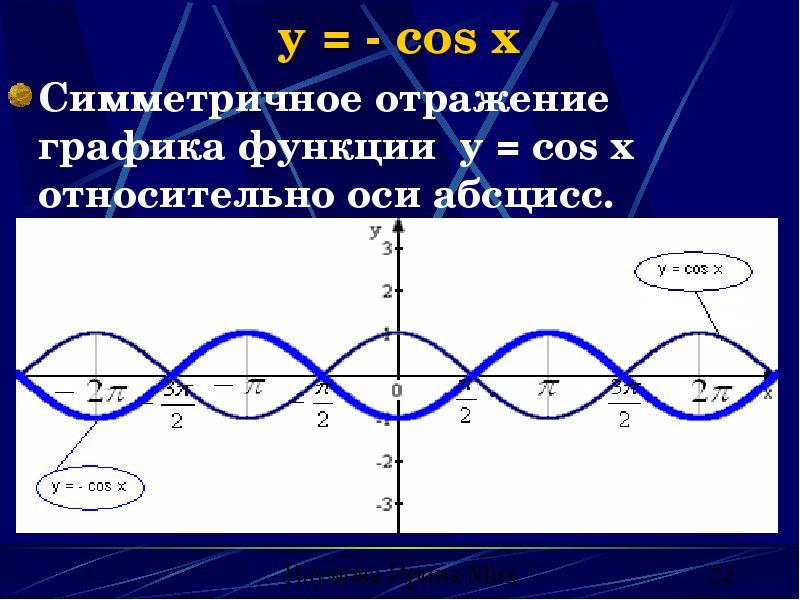
y = - cos x Симметричное отражение графика функции y = cos x относительно оси абсцисс.

y = - cos x (свойства) Изменяются промежутки возрастания (убывания); промежутки положительных (отрицательных) значений. Функция возрастает на отрезке 0;  и на отрезках, получаемых сдвигами этого отрезка на 2n, n = 1, 2, 3… Функция убывает на отрезке ; 2 и на отрезках, получаемых сдвигами этого отрезка на 2n, n = 1, 2, 3… Функция принимает положительные значения на интервале (/2; 3/2) и на интервалах, получаемых сдвигами этого интервала на 2n, n = 1, 2… Функция принимает отрицательные значения на интервале (- /2; /2) и на интервалах, получаемых сдвигами этого интервала на 2n, n = 1, 2…

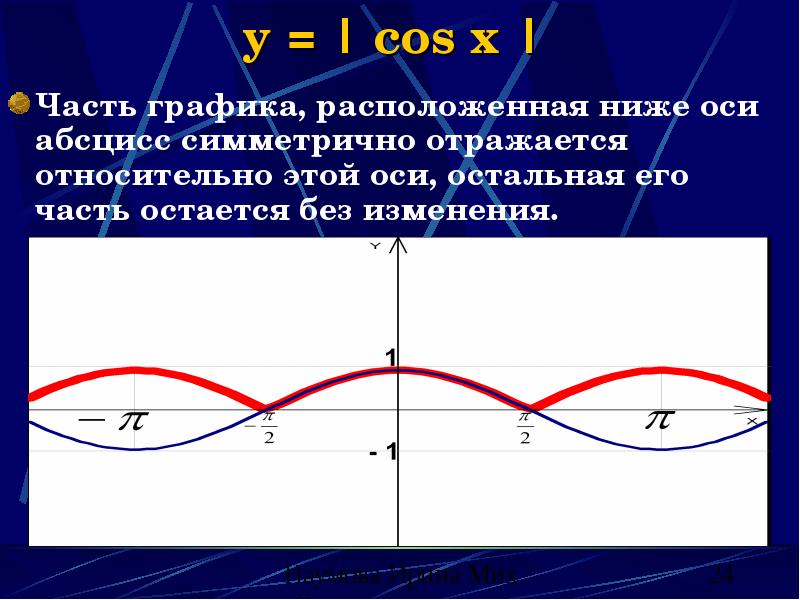
y = | cos x | Часть графика, расположенная ниже оси абсцисс симметрично отражается относительно этой оси, остальная его часть остается без изменения.

y = |cos x| (свойства) Изменяются: множество значений функции; период; промежутки возрастания (убывания); наибольшее (наименьшее) значение. E (f): y [ 0; 1] Периодичность: Т =  Функция возрастает на промежутке (/2; )+ сдвиги на n, nZ Функция убывает на промежутке (0; /2) + сдвиги на n, nZ f (x) > 0: при любом значении х f (x) < 0: нет y (наиб) = 1, при х = 2n, nZ y (наим) = 0, при х = /2 + n, nZ

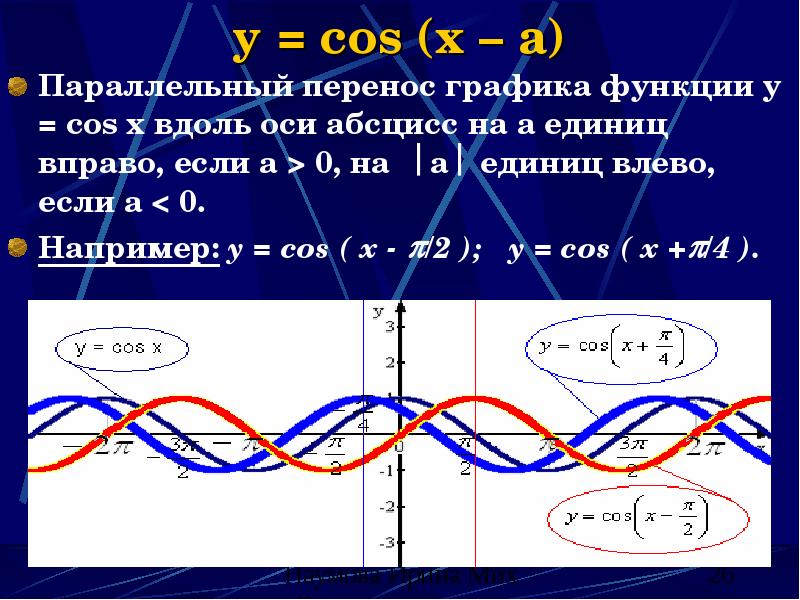
y = cos (x – a) Параллельный перенос графика функции y = cos x вдоль оси абсцисс на а единиц вправо, если а > 0, на а  единиц влево, если а < 0. Например: y = cos ( x - /2 ); y = cos ( x +/4 ).

y = cos (x – a) (свойства) Изменяются: четность; промежутки возрастания (убывания); нули функции; промежутки положительных (отрицательных) значений. Например: y = cos (x + /4) Четность: f (x)  f (-x)  -f (x), т.к. cos (-(x + /4)) = cos (-x - /4) Функция возрастает на [ 3/4; 11/4] + сдвиги на 2n, nZ Функция убывает на [-/4; 3/4 ]+ сдвиги на 2n, nZ f (x) =0 при х = /4 +n, nZ f (x) > 0 при х (-3/4; /4) + сдвиги на 2n, nZ f( (x) <0 при х (/4; 5/4) + сдвиги на 2n, nZ

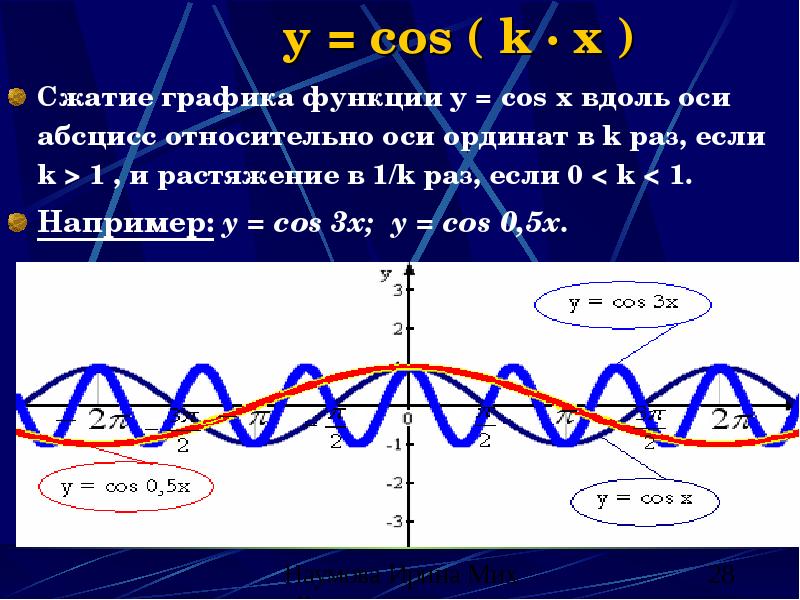
y = cos ( k · x ) Сжатие графика функции y = cos x вдоль оси абсцисс относительно оси ординат в k раз, если k > 1 , и растяжение в 1/k раз, если 0 < k < 1. Например: y = cos 3x; y = cos 0,5x.

y = cos ( k · x ) (свойства) Изменяются: период; промежутки возрастания (убывания); нули функции; промежутки положительных (отрицательных) значений. Например: y = cos 3x Период: Т = 2/3, (т.к. наименьший положительный период функции y = cos x равен 2, то 3Т = 2  Т = 2/3). Функция возрастает на /3; 2/3 + сдвиги на 2n/3, nZ. Функция убывает на 0; /3 + сдвиги на 2n/3, nZ. f (x) = 0 при х = /6 + n/3. f (x) > 0 при х (-/6; /6) + сдвиги на 2n/3, n  Z. f (x) < 0 при х (/6; /2) + сдвиги на 2n/3, n  Z.

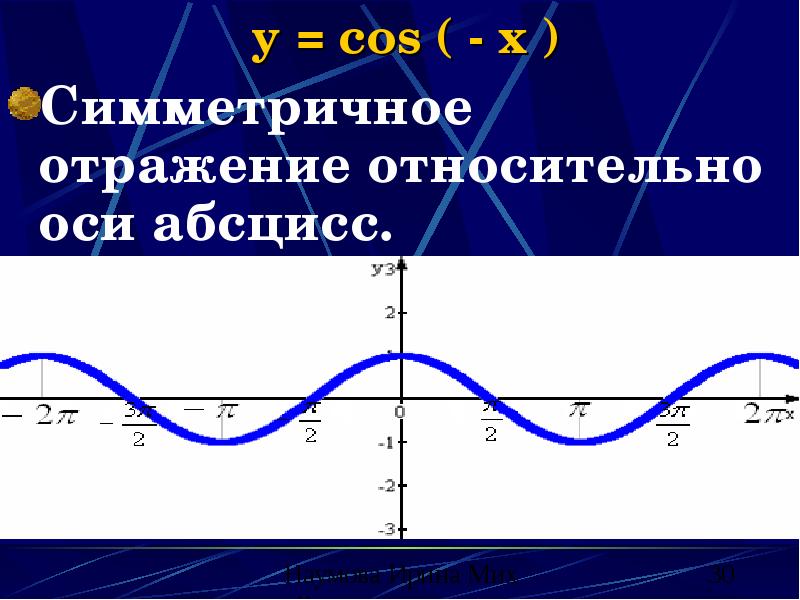
y = cos ( - x ) Симметричное отражение относительно оси абсцисс.

y = cos (-x) (свойства) В данном случае свойства функции не меняются, так как функция y = cos x – четная и cos (-x) = cos (x)  все свойства функции y = cos x справедливы и для функции y = cos (-x)

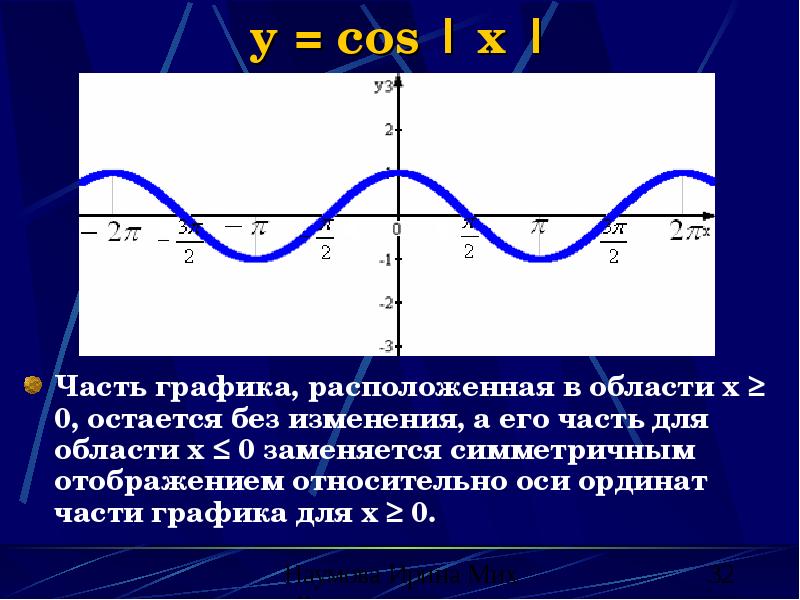
y = cos | x | Часть графика, расположенная в области х  0, остается без изменения, а его часть для области х  0 заменяется симметричным отображением относительно оси ординат части графика для х  0.

y = cos|x| (свойства) В данном случае свойства функции не меняются, так как функция y = cos x – четная и cos |x| = cos (-x) = cos (x)  все свойства функции y = cos x справедливы и для функции y = cos |x|

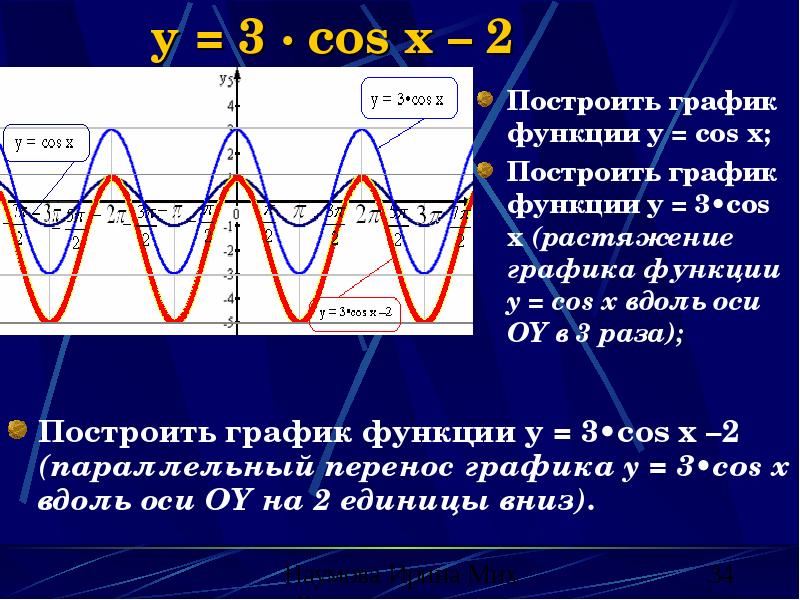
y = 3 · cos x – 2 Построить график функции y = 3•cos x –2 (параллельный перенос графика y = 3•cos x вдоль оси OY на 2 единицы вниз).

Свойства функции y = 3 · cos x – 2 Область определения: D(f): х  R; Множество значений: y  [- 5; 1], т.к. –1  cos x  1  - 3  3cos x  3  - 5  3cos x – 2  1; Периодичность: Т = 2; Четность: четная, т.к. 3сos (-x) –2 = 3cos x – 2  график функции симметричен относительно оси OY; Возрастает: на отрезке [; 2] и на отрезках, получаемых сдвигами этого отрезка на 2n, n = 1, 2; 3…; Убывает: на отрезке [0;  и на отрезках, получаемых сдвигами этого отрезка на 2n, n = 1, 2, 3…

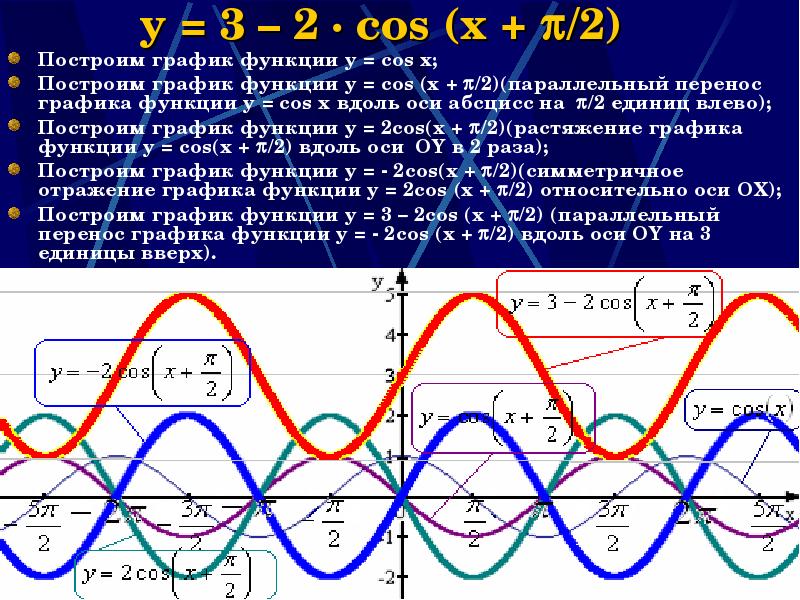
y = 3 – 2 · cos (x + /2) Построим график функции y = cos x; Построим график функции y = cos (x + /2)(параллельный перенос графика функции y = cos x вдоль оси абсцисс на /2 единиц влево); Построим график функции y = 2cos(x + /2)(растяжение графика функции y = cos(x + /2) вдоль оси OY в 2 раза); Построим график функции y = - 2cos(x + /2)(симметричное отражение графика функции y = 2cos (x + /2) относительно оси OX); Построим график функции y = 3 – 2cos (x + /2) (параллельный перенос графика функции y = - 2cos (x + /2) вдоль оси OY на 3 единицы вверх).

Свойства функции y = 3 – 2 · cos (x + /2) Область определения: D(f): x  R; Множество значений: y   1; 5, т.к. –1  cos (x + /2)  1  –2  2cos (x + /2)  2  1  3 – 2cos (x + /2)  5; Периодичность: Т = 2; Четность: ни четная, ни нечетная, т.к. у(-х)  у(х)  -у (х) (график не симметричен ни оси OY, ни началу координат ) Возрастает: на 3/2; 5/2 и на отрезках, получаемых сдвигами этого отрезка на 2n, n = 1, 2, 3… Убывает: на /2; 3/2 и на отрезках, получаемых сдвигами этого отрезка на 2n, n = 1, 2, 3… Функция принимает значения равные: нулю: нет (уравнение 3 – 2cos( x + /2) = 0 не имеет корней т.к.|- 3/2| > 1); положительные: при любом х; наибольшее, равное 5: при x = /2 + 2n, n  Z. наименьшее, равное 1: при х = - /2 + 2n, n  Z.