Кратные и Двойные интегралы

Кратные интегралы Как известно, интегрирование является процессом суммирования. Однако суммирование может производится неоднократно, что приводит нас к понятию кратных интегралов. Рассмотрение этого вопроса начнем с рассмотрения двойных интегралов.

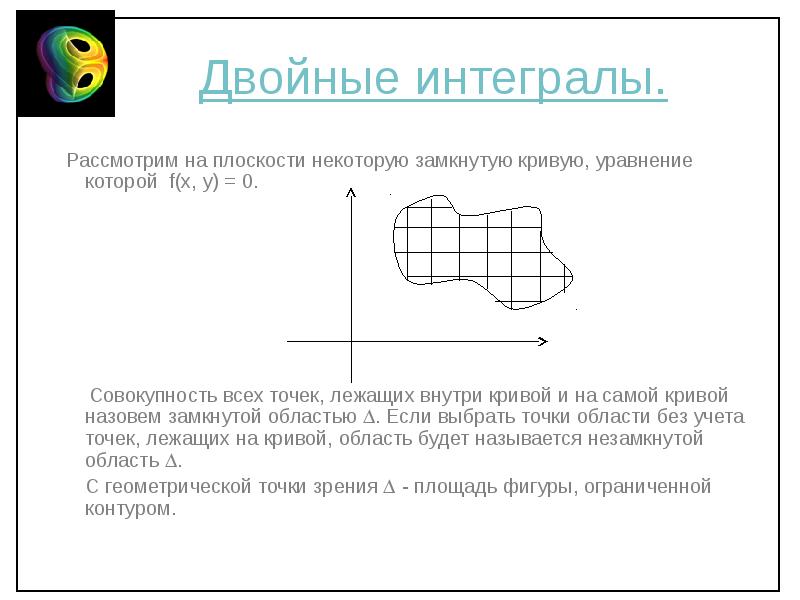
Двойные интегралы. Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0. Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью . Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область . С геометрической точки зрения  - площадь фигуры, ограниченной контуром.

Разобьем область  на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние , а по оси у – на . Вообще говоря, такой порядок разбиения необязателен, возможно разбиение области на частичные участки произвольной формы и размера. Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны В каждой частичной области возьмем произвольную точку и составим интегральную сумму где f – функция непрерывная и однозначная для всех точек области . Если бесконечно увеличивать количество частичных областей i, тогда, очевидно, площадь каждого частичного участка Si стремится к нулю.

Определение Если при стремлении к нулю шага разбиения области  интегральные суммы имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области . учетом того, что получаем: В приведенной выше записи имеются два знака , т.к. суммирование производится по двум переменным х и у. Т.к. деление области интегрирования произвольно, также произволен и выбор точек , то, считая все площади одинаковыми, получаем формулу:

Условия существования двойного интеграла Сформулируем достаточные условия существования двойного интеграла Теорема. Если функция f(x, y) непрерывна в замкнутой области , то двойной интеграл существует.

Теорема Если функция f(x, y) ограничена в замкнутой области  и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл существует.

Свойства двойного интеграла. 1) 2) 3) Если  = 1 + 2, то 4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования. 5) Если f(x, y)  0 в области , то 6) Если f1(x, y)  f2(x, y), то 7)

Вычисление двойного интеграла Теорема Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями х = a, x = b, (a < b), y = (x), y = (x), где  и  - непрерывные функции и   , тогда

Теорема. Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями y = c, y = d (c < d), x = (y), x = (y) ((y)  (y)), то

Замена переменных в двойном интеграле Расмотрим двойной интеграл вида , где переменная изменяется в пределах от a до b, а переменная – от до Положим Тогда

т.к. при первом интегрировании переменная принимается за постоянную, то т.к. при первом интегрировании переменная принимается за постоянную, то подставляя это выражение в записанное выше соотношение для , получаем:

Выражение называется определителем Якоби или Якобианом функций и Выражение называется определителем Якоби или Якобианом функций и (Якоби Карл Густав Якоб – (1804-1851) – немецкий математик) Тогда Т.к. при первом интегрировании приведенное выше выражение для принимает вид ( при первом интегрировании полагаем ), то при изменении порядка интегрирования, получаем соотношение:

Двойной интеграл в полярных координатах. Воспользуемся формулой замены переменных: При этом известно, что В этом случае Якобиан имеет вид: Тогда Здесь  - новая область значений,