Применения производной к исследованию функций

Применения производной к исследованию функций

Оглавление Схема исследования функций; Признак возрастания (убывания) функции: Достаточный признак возрастания функции; Достаточный признак убывания функции; Критические точки функции: Необходимое условие экстремума; Признак максимума функции; Признак минимума функции.

Схема исследования функций Найти области определения и значений данной функции f. Выяснить, обладает ли функция особенностями, облегчающими исследование. Вычислить координаты точек пересечения графика с осями координат. Найти промежутки знакопостоянства функции f. Выяснить, на каких промежутках функция f возрастает, а на каких убывает. Найти точки и вид экстремума и вычислить значения f в этих точках. Исследовать поведение функции f в окрестности характерных точек, не входящих в область определения.

Признак возрастания (убывания) функции

Достаточный признак возрастания функции. Если f´ (x) > 0 в каждой точке интервала I, то функция возрастает на I. Достаточный признак возрастания функции. Если f´ (x) > 0 в каждой точке интервала I, то функция возрастает на I. Достаточный признак убывания функции. Если f´ (х) < 0 в каждой точке интервала I, то функция убывает на I.

Доказательство признака возрастания (убывания) функции Доказательство проводится на основании формулы Лагранжа: f´

Пример нахождения промежутков возрастания (убывания) функции Дано: f (x) = -2x + sin x

Критические точки функции, максимумы и минимумы

Необходимое условие экстремума (теорема Ферма) Если точка х0 является точкой экстремума функции f и в этой точке существует производная f´, то она равна нулю: f´(х0) = 0

Теорема Ферма есть лишь необходимое условие экстремума. Из того, что производная в точке х0 обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум. Теорема Ферма есть лишь необходимое условие экстремума. Из того, что производная в точке х0 обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум.

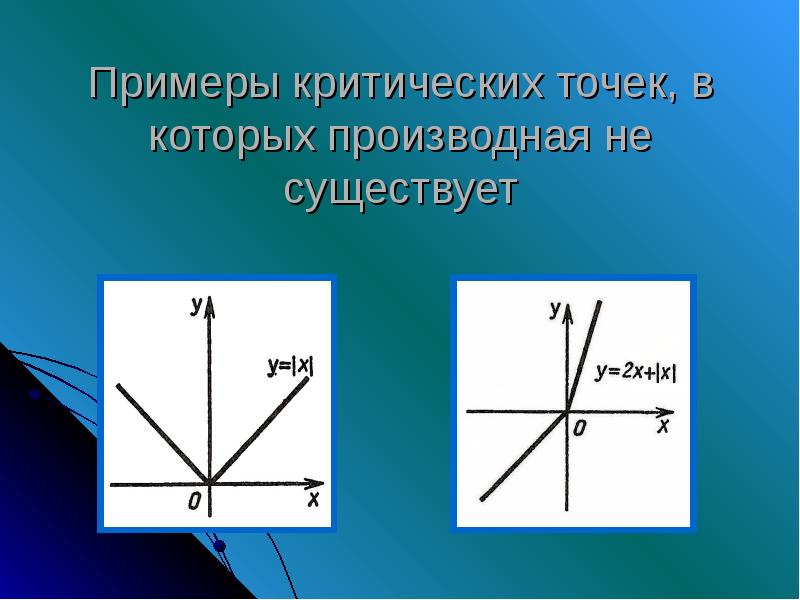
Примеры критических точек, в которых производная не существует

Признак максимума функции Если функция f непрерывна в точке х0, а f´ (х) > 0 на интервале (а; х0) и f´ (х) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f. Упрощённая формулировка признака: Если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.

Признак минимума функции Если функция f непрерывна в точке х0, f´ (х) < 0 на интервале (а; х0) и f´ (х) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f. Упрощённая формулировка признака: Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка максимума.

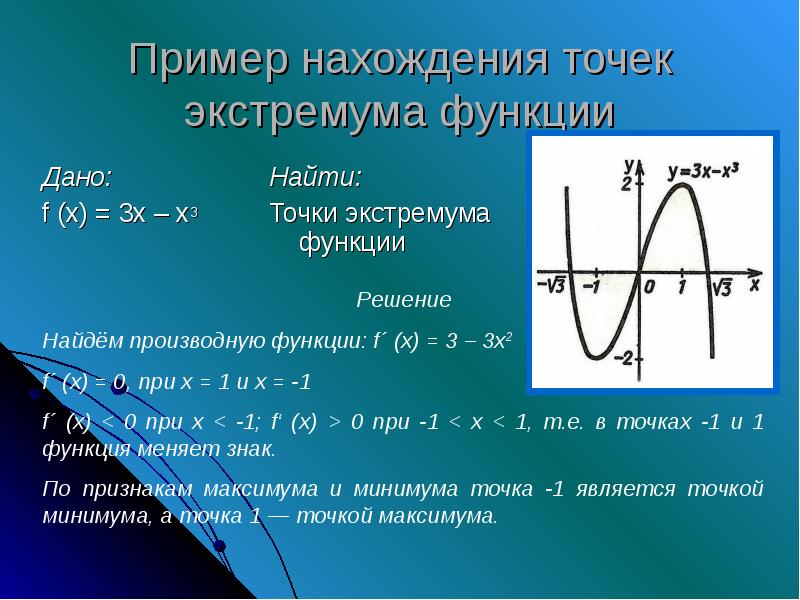
Пример нахождения точек экстремума функции Дано: f (x) = 3x – x3

Проект выполняла Сергеева Вероника, ученица 11 класса, с использованием следующих материалов: Алгебра и начала анализа. Учебник для 10-11 классов средней школы.