Methods of proof презентация

Methods of proof Irina Prosvirnina Some terminology Direct argument Contrapositive argument Proof by contradiction Mathematical induction

Some terminology A theorem is a statement that can be shown to be true. In mathematical writing, the term theorem is usually reserved for a statement that is considered at least somewhat important. Less important theorems sometimes are called propositions. A theorem may be the universal quantification of a conditional statement with one or more premises and a conclusion.

Терминология We demonstrate that a theorem is true with a proof. A proof is a valid argument that establishes the truth of a theorem.

Some terminology The statements used in a proof can include axioms (or postulates), which are statements we assume to be true, the premises, if any, of the theorem, and previously proven theorems.

Some terminology Axioms may be stated using primitive terms that do not require definition, but all other terms used in theorems and their proofs must be defined.

Some terminology Rules of inference, together with definitions of terms, are used to draw conclusions from other assertions, tying together the steps of a proof. In practice, the final step of a proof is usually just the conclusion of the theorem.

Some terminology A less important theorem that is helpful in the proof of other results is called a lemma (plural: lemmas or lemmata). Complicated proofs are usually easier to understand when they are proved using a series of lemmas, where each lemma is proved individually.

Some terminology A corollary is a theorem that can be established directly from a theorem that has been proved.

Some terminology A conjecture is a statement that is being proposed to be a true statement, usually on the basis of some partial evidence, a heuristic argument, or the intuition of an expert. When a proof of a conjecture is found, the conjecture becomes a theorem. Many times conjectures are shown to be false, so they are not theorems.

Methods of proof In practice, the proofs of theorems designed for human consumption are almost always informal proofs, where more than one rule of inference may be used in each step, where steps may be skipped, where the axioms being assumed and the rules of inference used are not explicitly stated.

Methods of proof Informal proofs can often explain to humans why theorems are true, while computers are perfectly happy producing formal proofs using automated reasoning systems.

Methods of proof The methods of proof discussed here are important not only because they are used to prove mathematical theorems, but also for their many applications to computer science. These applications include verifying that computer programs are correct, establishing that operating systems are secure, making inferences in artificial intelligence, showing that system specifications are consistent, and so on.

Methods of proof Consequently, understanding the techniques used in proofs is essential both in mathematics and in computer science.

Methods of proof Logical arguments are used to give us proofs of the theorems. In computing such proofs are essential in the design and verification of algorithms. The commonest types of proof are ones where we wish to establish the truth of a proposition of the form .

Methods of proof There are several standard methods of proof, including the following: direct argument, contrapositive argument, proof by contradiction.

Direct argument 1. Direct argument Assume is true and show that is true. This rules out the situation where is true and is false which is the only case where is false.

Contrapositive argument 2. Contrapositive argument Assume is false and show that is false. This demonstrates that is true which is the same as showing that is true.

Proof by contradiction 3. Proof by contradiction Assume is true and is false and derive a contradiction. This again rules out the situation where is true and is false which is the only case where is false.

Example 1 Use a direct method of proof to show that if х and у are odd integers, then ху is also odd. Solution First, notice that if x is an odd integer then х = 2т + 1, where т is an integer.Similarly, у = 2n + 1 for some integer n. Then, ху = (2m + 1)(2n + 1)= = 4mn + 2m + 2 + 1 = = 2(2mn + m + n) + 1 Is an odd integer.

Example 2 Let n be a positive integer. Prove, using the contrapositive, that if n2 is odd, then n is odd. Solution The negation of n2 is odd is n2 is even, and the negation of n is odd is n is even. Therefore, we proof directly that if n is even then n2 is even Since n is even, we can write n = 2m for some integer m. Then, n2 = 4m2 = 2(2m2) is also even.

Example 3 Use a proof by contradiction to show that if x2 = 2 then x is not a fraction. Solution By way of contradiction, assume that х is a fraction and write х = m/n where n and m are integers, n is not equal to 0 and n and m have no common factors. Since x2 = 2, we have that (m/n)2 = 2. Therefore, m2 = 2 n2. But this implies that m2 is an even integer. Therefore, т is an even integer. Hence, т = 2р for some other integer р.

Example 3 Use a proof by contradiction to show that if x2 = 2 then x is not a fraction. Solution Substituting this information into the equation m2 = 2 n2 leads to 4 p2 = 2 n2, n2 = 2 p2. But then, n is also an even integer. We have shown that m and n have a common factor (of 2) which contradicts our original assertion that m and n have no common factors. This contradiction can only be resolved by concluding that if x2 = 2 then x is not a fraction.

Mathematical induction In computing a program is said to be correct if it behaves in accordance with its specification. Whereas program testing shows that selected input values give acceptable output values, proof of correctness uses formal logic to prove that for any input values, the output values are correct. Proving the correctness of algorithms containing loops requires a powerful method of proof called mathematical induction.

Mathematical induction Consider the following recursive algorithm, intended to calculate the maximum element in a list a1, a2, …, an of positive integers. begin г:=0; М:=0; while г < n do begin r :=r+1; M:=max(M, ar); end еnd

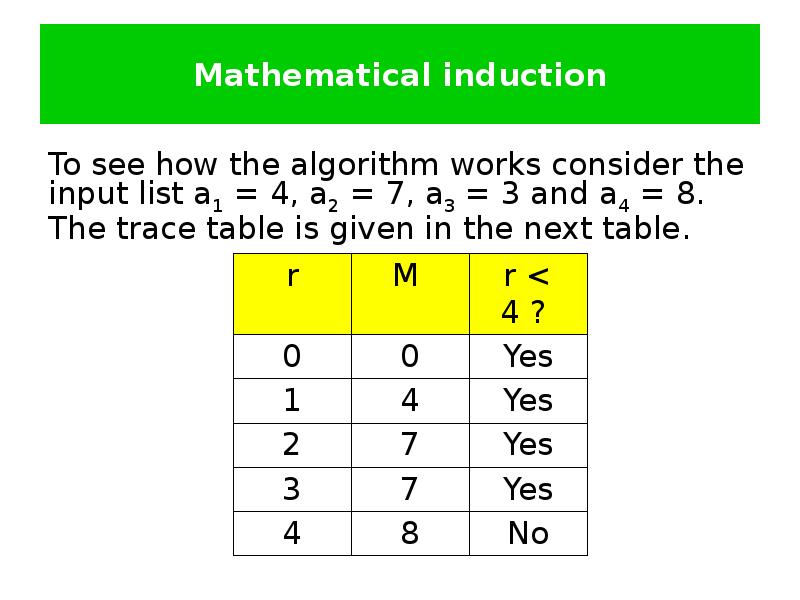
Mathematical induction To see how the algorithm works consider the input list a1 = 4, a2 = 7, a3 = 3 and a4 = 8. The trace table is given in the next table.

Mathematical induction The output is М = 8, which is correct. Notice that after each execution of the loop, М is the maximum of the elements of the list so far considered.

Mathematical induction So does the algorithm for all lists of any length n? Consider an input a1, a2, …, an of length n and let Mk be the value of М after k executions of the loop. For an input list a1 of length 1, the loop is executed once and M is assigned to be the maximum of 0 and a1,which is just a1. It is the correct input. If after k executions of the loop, Mk is the maximum element of the list a1, a2, …, ak then after one more loop Mk+1 is assigned the value max(Mk, ak+1 ) which will then be the maximum element of the list a1, a2, …, ak+1.

Mathematical induction By condition 1) the algorithm works for any list of length 1, and so by condition 2) it works for any list of length 2. By condition 2) again it works for any list of length 3, and so on. Hence, the algorithm works for any list of length n and so the algorithm is correct. This process can be formalised as follows.

Mathematical induction The principle of mathematical induction Let Р(n) be a predicate that is defined for all natural n. Suppose that Р(1) is true and For all 1 (Р(к) Р(k+1)) is true. Then Р(n) is true for all n 1.

Mathematical induction Example 1 Prove, by induction, that for all n 1 1+ 2 + … + n = n(n+1)/2. Solution Let Р(n) be the predicate 1+ 2 + … + n = n(n+1)/2. In the case n = 1, the left-hand side is simply 1, and the right-hand side is 1(1+1)/2 = 1. Therefore, Р(1) is true.

Mathematical induction Assume now that 1+ 2 + … + k = k(k+1)/2 for some k 1. Then 1+ 2 + … + (k+1) = (1+ 2 + … +k) + (k+1) = k(k+1)/2 + (k+1) = (k(k+1) + 2(k+1))/2 = ((k+2)(k+1))/2 = (k+1)(k+2)/2 . Hence, for all k 1(Р(k) Р(k+1)) is true. Therefore, by induction Р(n) is true for all n 1.

Mathematical induction Example 2 Prove, by induction, that 7n – 1 is divisible by 6 for all n 1. Solution First, note that an integer a is divisible by an integer b if there is some other integer m with а = mb. For example, 51 is divisible by 17 since 51 = 3 • 17. Let Р(n) be the predicate «7n – 1 is divisible by 6». In the case n = 1, 7n – 1 = 71 – 1 = 7 – 1 = 6, which is clearly divisible by 6. Therefore, Р(1) is true.

Mathematical induction Assume now that 7k – 1 is divisible by 6 for some k 1. Then, 7k+1 – 1 = 7(7k) – 1 = 7(7k – 1) + 7 – 1 = 7(7k – 1) + 6 . Since 7k – 1 is divisible by 6 it follows that 7(7k – 1) + 6 is also is divisible by 6. Hence, 7k+1 – 1 is divisible by 6 and so (Р(k) Р(k+1)) for all k 1 is true. Therefore, by induction Р(n) is true for all n 1.

Mathematical induction Example 3 A sequence of integers x1, x2, …, xn is defined recursively as follows: x1 = 1 and xk+1 = xk + 8k for к >= 1. Prove that xn = (2n – 1)2 for all n >= 1. Solution Let Р(n) be the predicate xn = (2n – 1)2. In the case n = 1, (2n – 1)2 = (2 • 1 – 1)2 = 1. Therefore, Р(1) is true.

Mathematical induction Assume now that xk = (2k – 1)2 for some k 1. Then xk+1 = xk + 8k = (2k – 1)2 + 8k = 4k2 + 4k + 1 = (2k + 1)2 . Hence, xk+1 = (2(k + 1) – 1)2 . And so (Р(k) Р(k+1)) is true for all k 1. Therefore, by induction Р(n) is true for all n 1.