The mean values презентация
Содержание
- 2. Part 1 THE MEAN VALUES
- 3. СHAPTER QUESTIONS Measures of location Types of means Measures of location
- 7. What is the mean? The mean - is a general indicator
- 8. Statistics derive the formula of the means of the formula of
- 9. There are the following types of mean: There are the
- 10. The higher the degree of z, the greater the value of
- 11. There are two ways of calculating mean: There are two ways
- 12. Types of means
- 13. Arithmetic mean Arithmetic mean value is called the mean value of
- 14. Characteristics of the arithmetic mean The arithmetic mean has a
- 15. 2. If the data values (Xi) divided or multiplied by a
- 16. 3. If the frequency divided by a constant number, the mean
- 17. 4. Multiplying the mean for the amount of frequency equal to
- 18. 5.The sum of the deviations of the number in a data
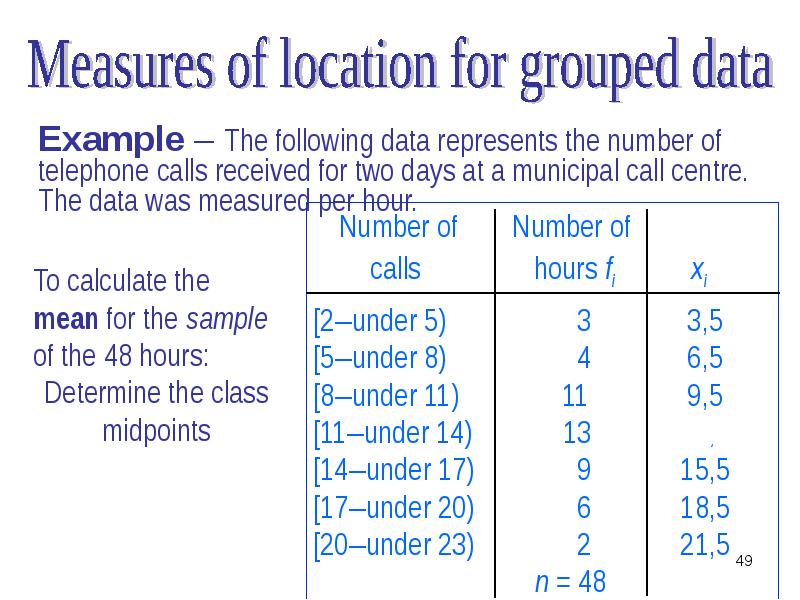
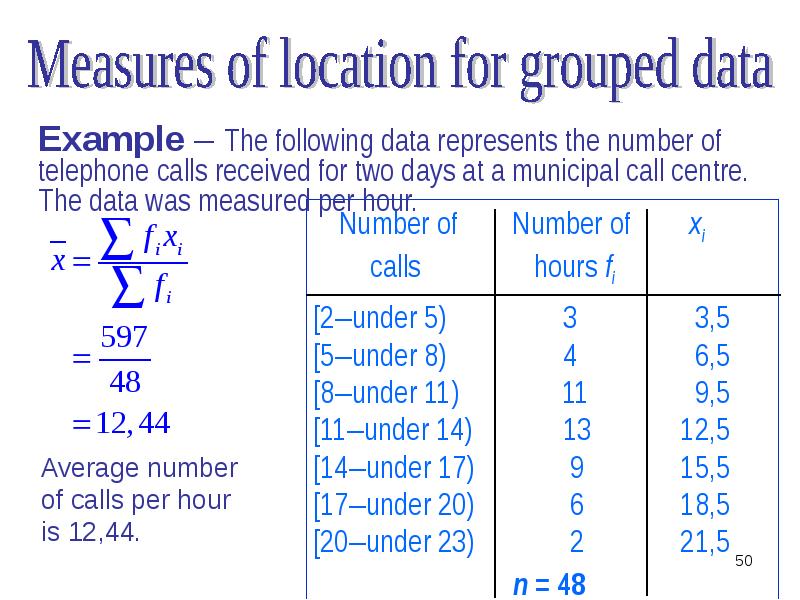
- 19. Measures of location for ungrouped data In calculating summary values for
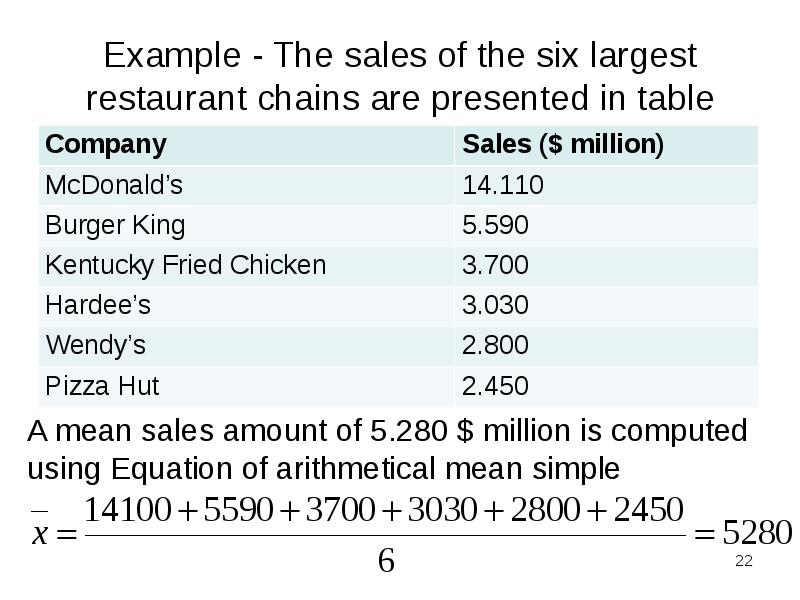
- 22. Example - The sales of the six largest restaurant chains are
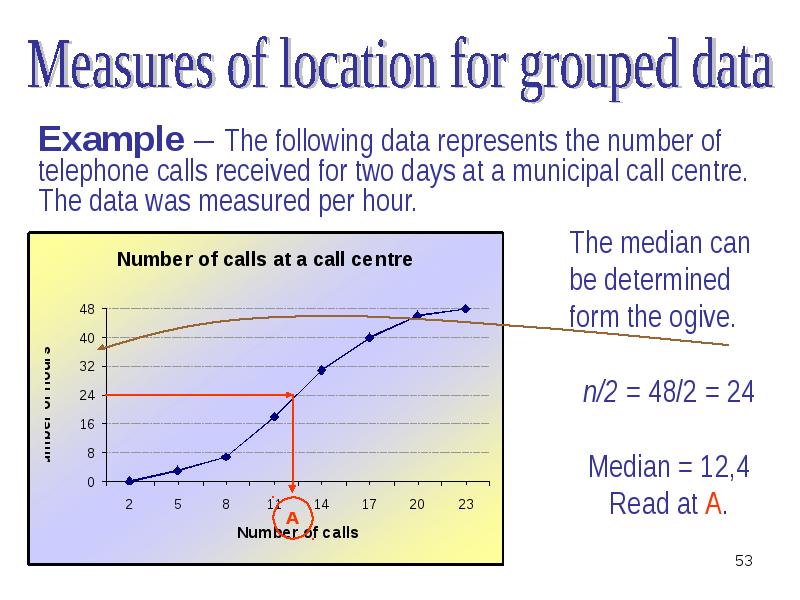
- 23. MEDIAN for ungrouped data The median of a data is the
- 25. Position of median If n is odd: Median item
- 26. Example The median number of people treated daily at the
- 33. Is used if М = const: Is used if М =
- 34. For example: One student spends on a solution of task
- 35. Geometric mean for ungrouped data This value is used as the
- 36. Where П – the multiplication of the data value (Xi).
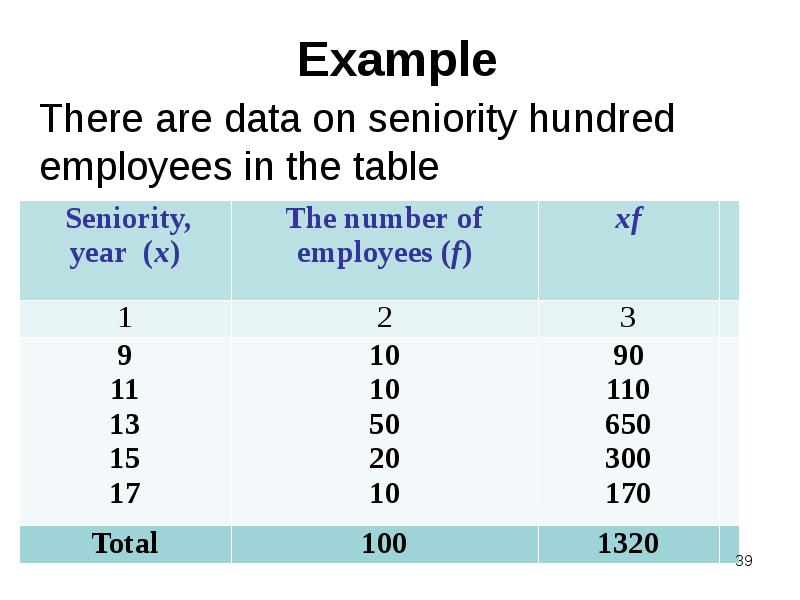
- 39. Example
- 40. Average seniority employee is: Average seniority employee is:
- 41. Harmonic mean for grouped data Harmonic mean - is the reciprocal
- 42. Harmonic mean for grouped data Harmonic mean is calculated by the
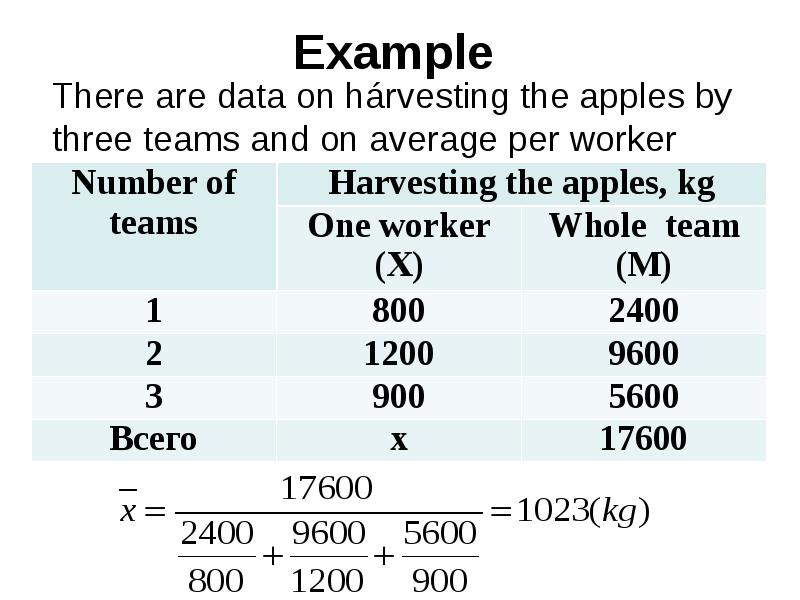
- 43. Example
- 44. is calculated by the formula: is calculated by the formula:
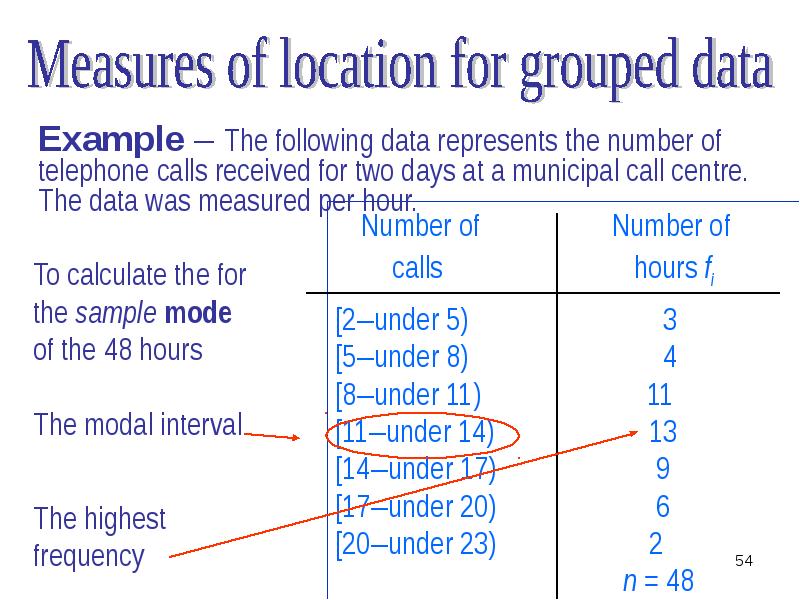
- 48. Mode is calculated by the formula: Mode is calculated by the
- 55. We substitute the data into the formula: We substitute the data
- 57. Relationship between mean, median, and mode If a distribution is symmetrical:
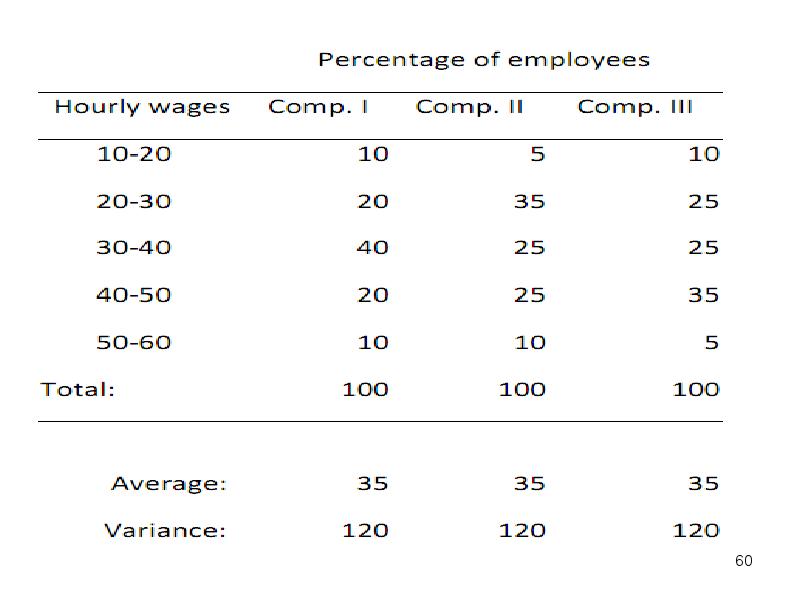
- 59. EXAMPLE Consider a study of the hourly wage rates in three
- 61. So we have three 100-element samples, which have the same average
- 62. The histogram for company I (left chart) is symmetric. The histogram
- 63. Knowing the median, modal and average values enables us to resolve
- 64. We obtain the following relevant indicators (measures) of asymmetry: We
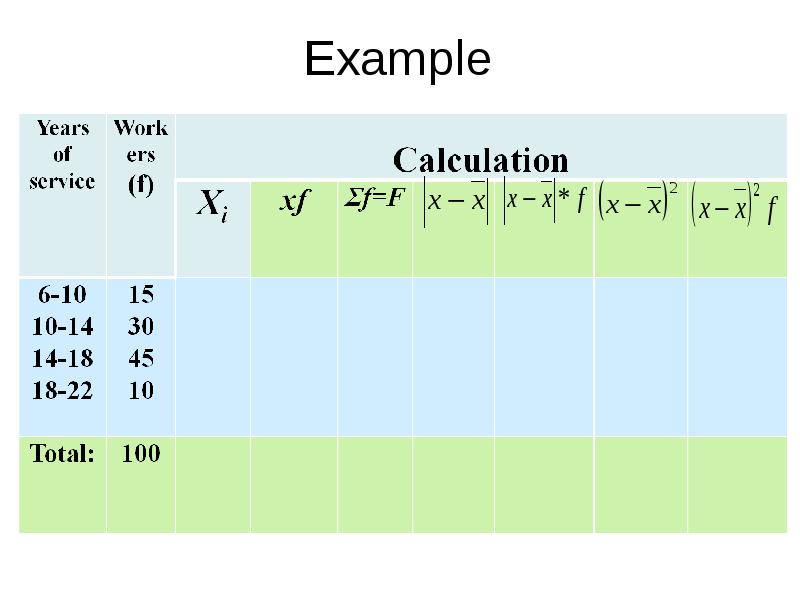
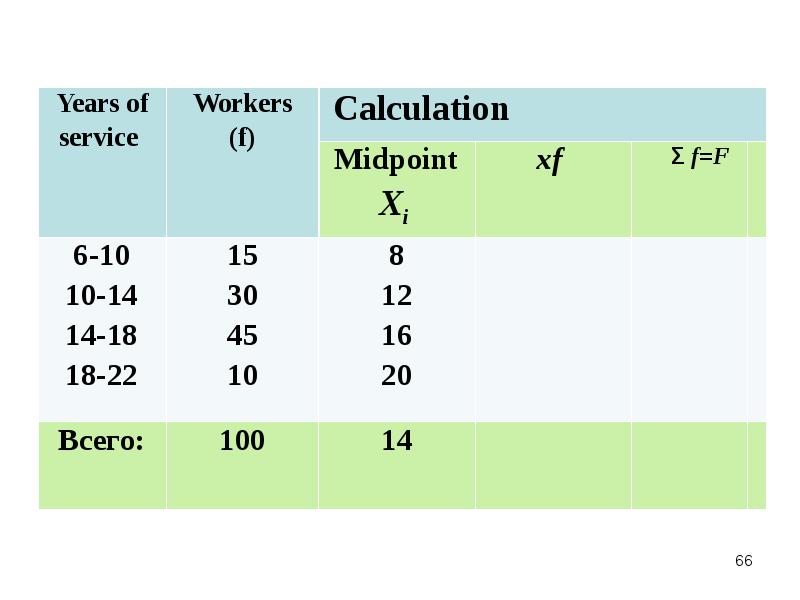
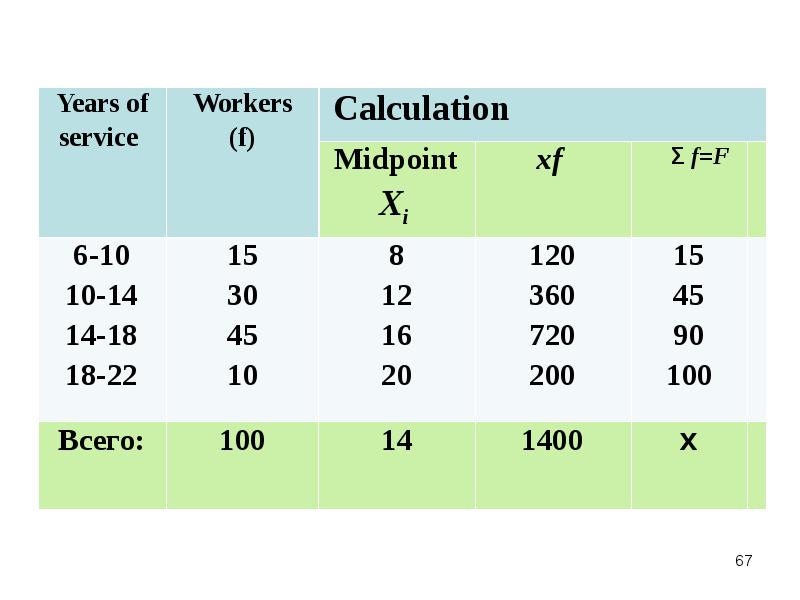
- 65. Example
- 68. The weighted arithmetic mean The weighted arithmetic mean
- 69. The median
- 70. The mode
- 72. Скачать презентацию









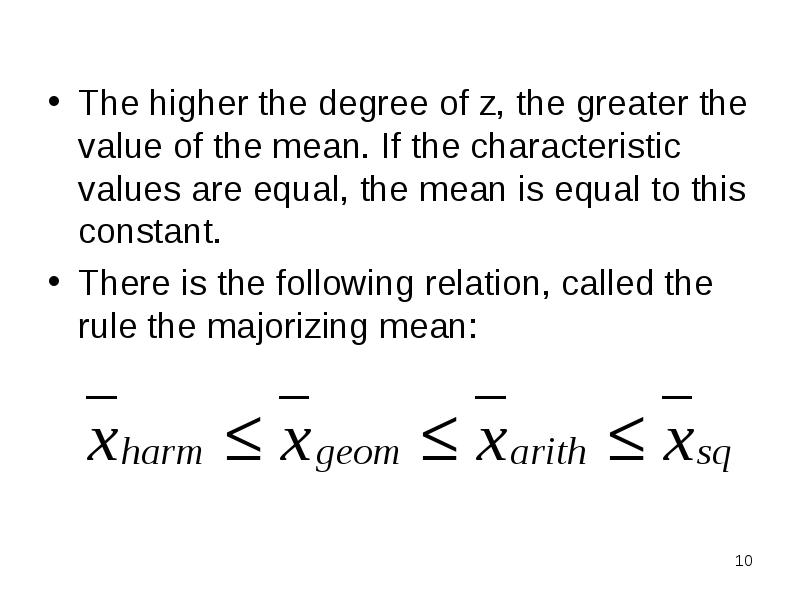





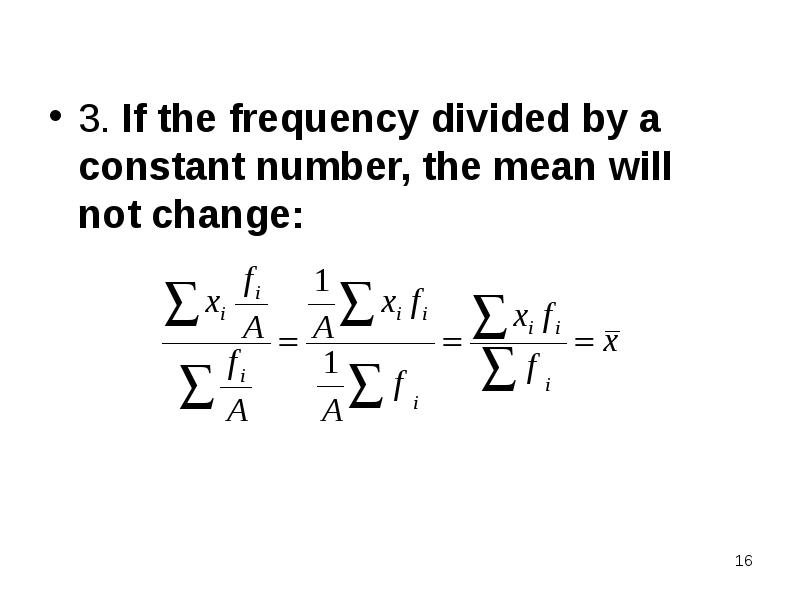








































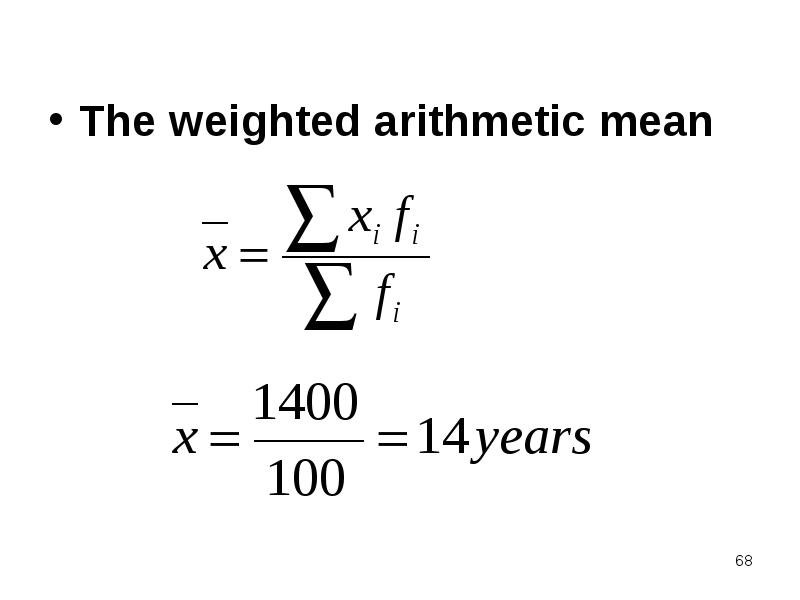
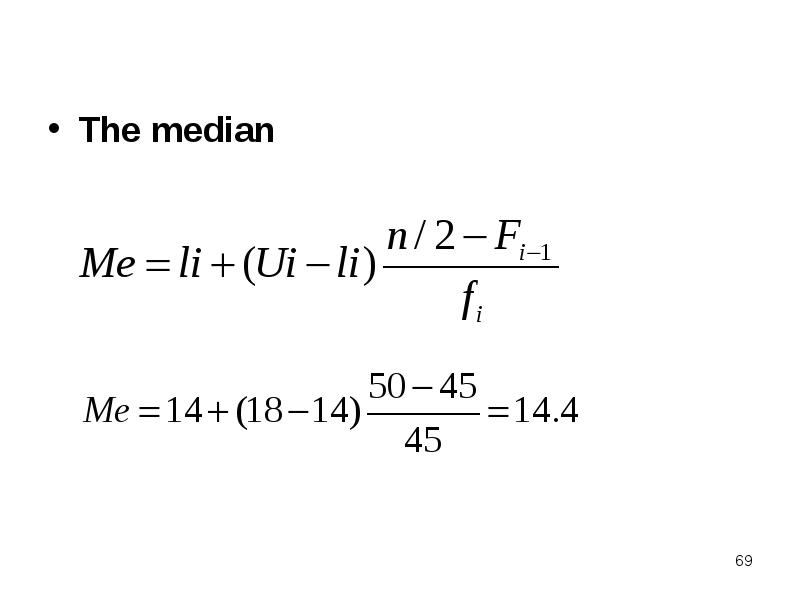


Слайды и текст этой презентации
Похожие презентации